机器学习——Logistic回归

一、Logistic回归模型

1、什么是Logistic回归模型及其实现原理

逻辑回归是一种广义的线性回归分析模型，主要用于数据挖掘、疾病自动诊断、经济预测等领域。它是一种监督学习下的机器学习算法，特别适用于解决二分类问题，尽管它也可以用于多分类问题。逻辑回归的核心在于使用Sigmoid函数将线性回归的结果映射到(0,1)的范围内，从而表示属于某一类别的概率。具体来说，如果Sigmoid函数的输出值大于0.5，则分类为1（或某一类别），否则分类为0（或另一类别）。

2、线性回归

在逻辑回归模型中,我们假设输入特征

输出标签

之间存在一个线性关系:

 

其中，

是模型的权重参数,表示每个特征对输出的贡献程度。

是模型的偏差参数,表示输出的基准值，是线性组合的结果,是一个实数值。

这个线性组合 就是逻辑回归模型的中间输出。接下来,我们使用 sigmoid 函数将 映射到 之间,得到最终的概率输出:

这个概率输出表示样本属于正类的概率。通常情况下,我们会将概率阈值设为 0.5,将高于 0.5 的样本预测为正类,低于 0.5 的样本预测为负类。

总之,线性组合是逻辑回归模型的核心计算步骤。它将输入特征和模型参数相结合,得到一个中间的实数值。然后通过 sigmoid 函数,将这个中间值转换为 0 到 1 之间的概率输出,完成分类任务。

3、Sigmoid函数

Sigmoid公式：

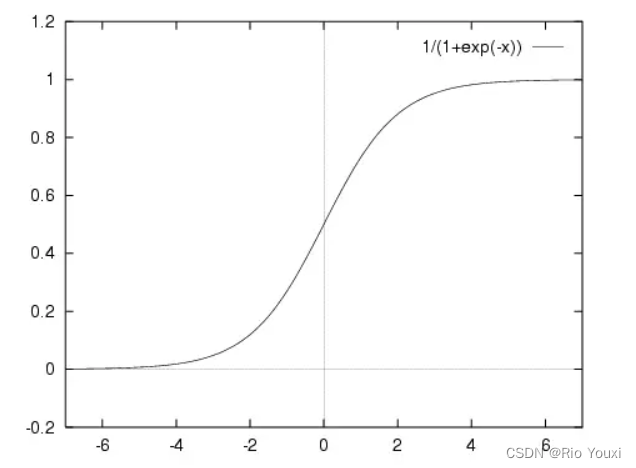
Sigmoid函数是逻辑回归模型的核心组成部分,它将线性模型的输出转换为概率值,为分类任务提供了合理的概率解释。

sigmoid函数有以下几个重要特点:

1. 输出范围在 (0, 1) 之间,即 0 < s(z) < 1。这正好符合概率的性质,因此 sigmoid 函数常用于二分类问题中,将输出解释为样本属于正类的概率。

2. 当 z 趋于正无穷时,s(z) 趋于 1;当 z 趋于负无穷时,s(z) 趋于 0。这种 S 型曲线的特点非常适合建模事物发生的概率。

3. Sigmoid函数是连续可导的,这使得它在基于梯度的优化算法中很容易应用。

4、Logistic回归的优缺点

4.1 优点:

1. 简单易实现: 逻辑回归是一种相对简单的机器学习算法,其数学原理易于理解,实现起来也比较简单。

2. 可解释性强: 逻辑回归模型参数都有明确的物理意义,可以很好地解释每个特征对于预测结果的影响程度。这使得它在一些需要解释性的场景下很有优势。

3. 适用于二分类和多分类: 逻辑回归可以很方便地扩展到多分类任务,使用 softmax 函数即可实现。这使它成为一种通用的分类算法。

4.2 缺点：

1. 只能处理线性可分的数据: 逻辑回归假设输入特征和输出之间存在线性关系。如果数据分布复杂,呈现非线性关系,逻辑回归就无法很好地拟合。

2. 容易过拟合: 在特征维度较高或样本量较小的情况下,逻辑回归容易过拟合训练数据,泛化性能较差。需要采取正则化等措施来解决。

3. 对数据分布敏感: 逻辑回归要求输入特征服从某种概率分布,通常假设高斯分布。如果实际数据分布偏离这个假设,模型性能会受到影响。

二、利用极大似然得到最好的Logsitic函数

在逻辑回归中,我们希望找到一组最优的模型参数和,使得给定输入特征和预测输出的概率最大。这就是最大似然估计的目标。

具体步骤如下:

1. 假设样本服从伯努利分布,即对于二分类问题,输出 服从 分布,其中 是 sigmoid 函数输出的概率。

2. 对于一个样本 ,其似然函数为:
   

3. 整个推导过程为

   其中，，。

4. 通过反复迭代上述更新公式,直到收敛,我们就可以得到使对数似然函数最大化的最优模型参数 和 。这样得到的逻辑回归模型就是在最大似然估计意义下的最优模型。

三、梯度下降算法求解回归系数

梯度下降算法原理如下：

1、创建本次实验所要用到的数据集

 data = np.array([[ 1.72, 1.93, 1.  ],
                 [ 3.47, 2.04, 0.  ],
                 [ 4.75, 1.79, 1.  ],
                 [ 2.14, 1.25, 0.  ],
                 [ 2.72, 1.44, 0.  ],
                 [ 3.07, 1.98, 1.  ],
                 [ 4.42, 1.33, 1.  ],
                 [ 2.33, 2.22, 0.  ],
                 [ 3.63, 1.89, 1.  ],
                 [ 1.41, 1.60, 0.  ],
                 [ 2.06, 2.19, 0.  ],
                 [ 4.56, 1.77, 1.  ],
                 [ 3.98, 1.49, 1.  ],
                 [ 1.85, 2.36, 0.  ],
                 [ 2.53, 1.69, 0.  ],
                 [ 4.04, 1.91, 1.  ],
                 [ 1.55, 1.93, 0.  ],
                 [ 3.85, 2.11, 1.  ],
                 [ 4.88, 1.29, 1.  ],
                 [ 2.39, 2.36, 0.  ]])

其中，第一列表示该数据的横坐标，第二列表示该数据的纵坐标，第三列表示我们自己给定的该数据的类别，包括0类和1类。

2、定义Sigmoid函数和梯度下降函数计算权值并计算最小代价

def cost_function(theta, X, y):
    m = len(y)
    h = sigmoid(np.dot(X, theta))# 预测值
    return (-1/m) * (np.dot(y.T, np.log(h)) + np.dot((1-y).T, np.log(1-h))) 

def gradient_descent(X, y, theta, alpha, num_iters):
    m = len(y)
    J_history = np.zeros(num_iters)#创建一个数组，用于存储每次迭代后的代价函数值，以便观察算法的收敛情况。
    
    for i in range(num_iters):
        h = sigmoid(np.dot(X, theta))#计算当前参数 theta 下的预测值 h。
        theta = theta - (alpha/m) * np.dot(X.T, (h - y))#（h-y)计算预测值与真实标签之间的差值，表示预测误差.
        J_history[i] = cost_function(theta, X, y)#计算当前参数 theta 下的代价函数值，并存储到 J_history 数组中。
    
    return theta, J_history

3、对数据集进行分类、输出每个样本点的预测值并绘制拟合曲线

def plotBestFit(weights):
    X = data[:, :-1]#从 data 数组中提取特征数据，不包括最后一列（标签）
    y = data[:, -1]#从 data 数组中提取标签数据，即最后一列
    y_pred = np.round(sigmoid(np.dot(X, weights)))#使用训练后的参数 weights 对特征数据 X 进行预测，并将预测结果四舍五入到最近的整数，得到预测的标签 y_pred。
    accuracy = np.mean(y_pred == y)#计算预测标签 y_pred 与真实标签 y 之间的匹配率，即训练精度。
    print(f'训练后预测的准确性: {accuracy:.2f}')

    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(X[:, 0], X[:, 1], s=30, c=y, marker='o')

    x = np.arange(0, 3.0, 0.1)
    y = (-weights[0] - weights[1]*x)
    ax.plot(x, y)

    plt.xlabel('X1'); plt.ylabel('X2')
    plt.show()

运行结果如下：

拟合后的图像如下：

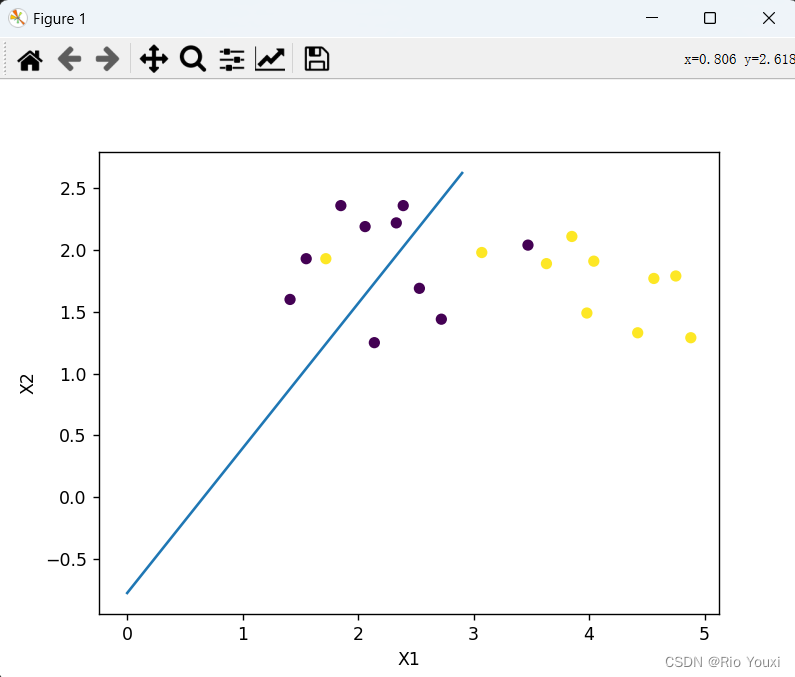
结果分析：逻辑回归输出的数值小于0.5的归为0类，大于0.5的归为1类，经过预测后发现有80%的样本点的预测类和实际类相等，所以该逻辑回归模型的预测正确率为0.80.

四、总结

通过本次实验，了解了什么是逻辑回归，即由线性回归+Sigmoid函数将数据映射到（0，1）之间，且可以将逻辑回归理解成概率空间的线性回归。了解了梯度下降算法的原理和实现，加深了各种优化算法的运用，提高了将优化算法运用到现实场景的基本理解。