第二章单变量线性回归

SqEEq

已于 2025-05-05 14:44:09 修改

阅读量830

点赞数 21

文章标签：机器学习笔记人工智能线性回归

于 2025-04-27 16:29:20 首次发布

本文链接：https://blog.csdn.net/m0_75164019/article/details/147563130

版权

一、线性回归模型（linear regression model）

该图再次解释了，在回归问题中，模型可以输出无限多可能的数据，而在分类问题中，模型会输出一组离散的、有限的可能输出。

机器学习的标准符号：

x：输入变量 / 特征 y：输出变量 / 目标变量 m: 训练样本的数量 (x, y)：单个训练样本 (x⁽ⁱ⁾,y⁽ⁱ⁾): 第i个训练样本

单变量线性回归模型的流程图和示例：

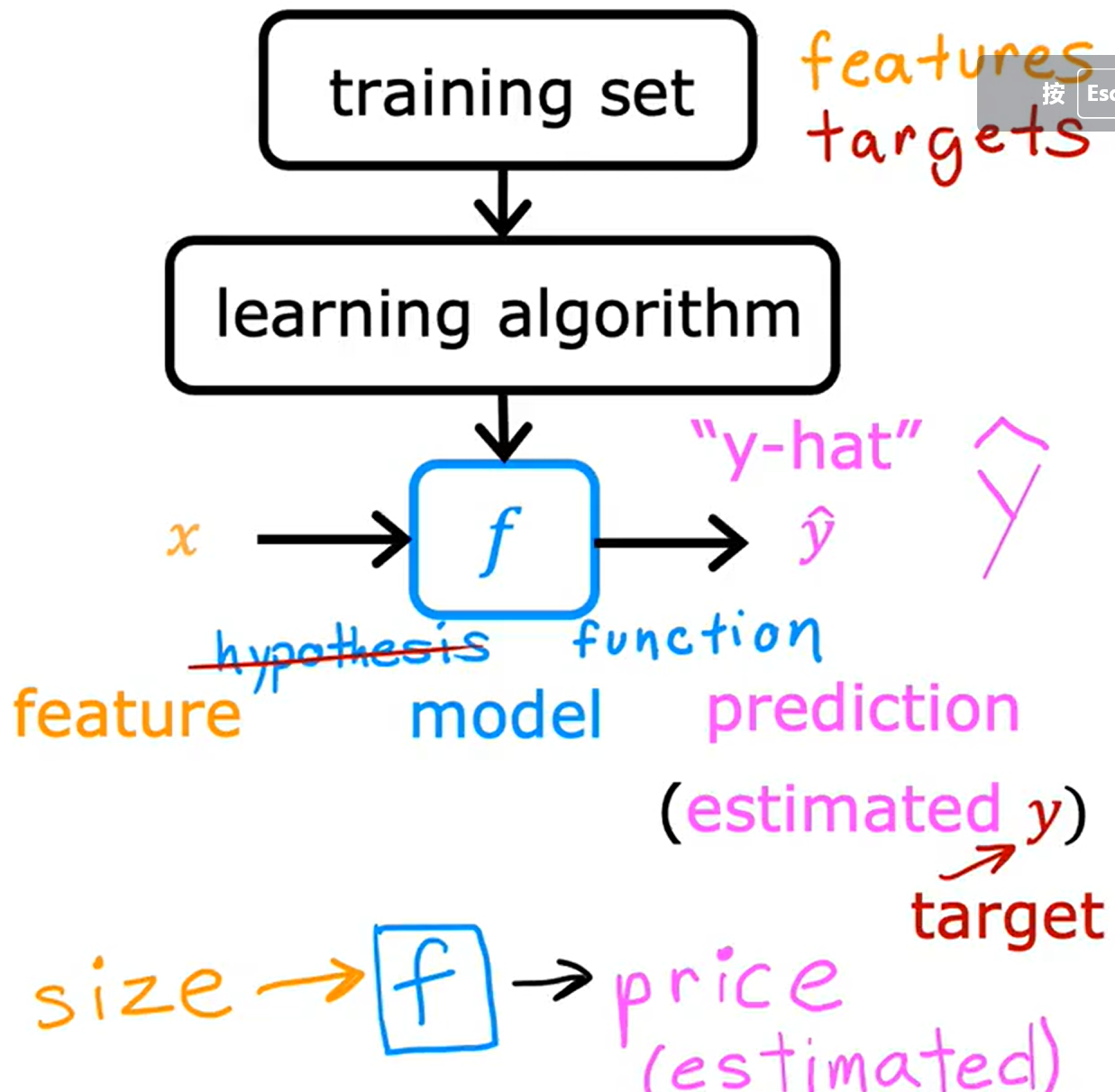
将训练样本集输入到学习算法中，再通过函数f即模型，输出一个 ŷ（y-hat)即真实值y的估计值，ŷ可能是真实值也可能不是真实值

本例中，只有一个x为单一变量，w和b为模型的参数也可以称为权重或者系数，是可以改变的定值（参数可以任意改变，但最终它是一个可知量，区别于未知的变量），所以该模型也成为单变量线性回归模型（univariate linear regression model）

为了实现线性回归，我们必须构建一个代价函数，代价函数通常用于线性回归和训练人工智能模型，通过代价函数我们将知晓模型的运行情况，以便于我们更好地进行模型训练。

二、代价函数（cost function）

代价函数的定义：

用来衡量模型在所有训练数据上的表现的函数。它的目标是量化模型的预测与实际标签之间的差距，从而为优化算法提供反馈，帮助模型调整参数以提高预测准确性。

回归问题中的代价函数：

我们假设一个函数f(x),其表达式为：

当我们输入x⁽ⁱ⁾时，根据之前的分析，我们将得到ŷ⁽ⁱ⁾，这个估计值ŷ⁽ⁱ⁾与y⁽ⁱ⁾（真实值）的差为误差（error），将其平方后再求和得到残差平方和（RSS），表达式为：

到这里为什么我们不用绝对值来表示这个误差值呢？

        对于误差取绝对值再求和的确方便了初期的求和计算，但是它将会产生下列的几个问题

1.数学上的可导性：

        平方的函数是光滑的且可导的，这对于优化算法（例如梯度下降）非常重要。在最小化RSS时，通常需要计算导数，如果使用绝对值，绝对值函数在0点不可导，这会导致在优化过程中出现不连续点，使得算法难以稳定收敛。

2.惩罚大偏差：

        平方会对较大的残差（即预测值与真实值之间的差异）给予更高的惩罚，这使得模型更倾向于减少大错误，而不仅仅是小错误。这样可以提高模型在整体上的拟合效果，避免某些异常值（离群点）对结果产生较小的影响。

3.数学简便性：

        对于平方的残差，解析求解（比如最小二乘法中的正规方程）比较简洁。使用绝对值会导致没有封闭解，并且在数学推导和计算上会变得复杂，因此平方更常用于实际应用中。

4.一致性和对称性：

        对于每个数据点，残差的平方是对正误差和负误差一视同仁的。绝对值虽然也有这个特性，但平方的计算性质更加简洁且容易进行优化。

再将残差平方和除以2m，即得到代价函数J(a,b)其表达式为：

变式为：

在这里除以m是为了让代价函数值不会随训练样本集的大小m的变大而变大（即计算平均平方误差或平均损失，使得代价函数与样本量无关），除以2是在之后计算其导数求梯度时简化数学公式。该代价函数是迄今为止线性回归最常用的函数。

我们的目标是让该函数值变小，使得模型的预测尽可能接近真实值。

2025.4.22

代价函数的直观理解：

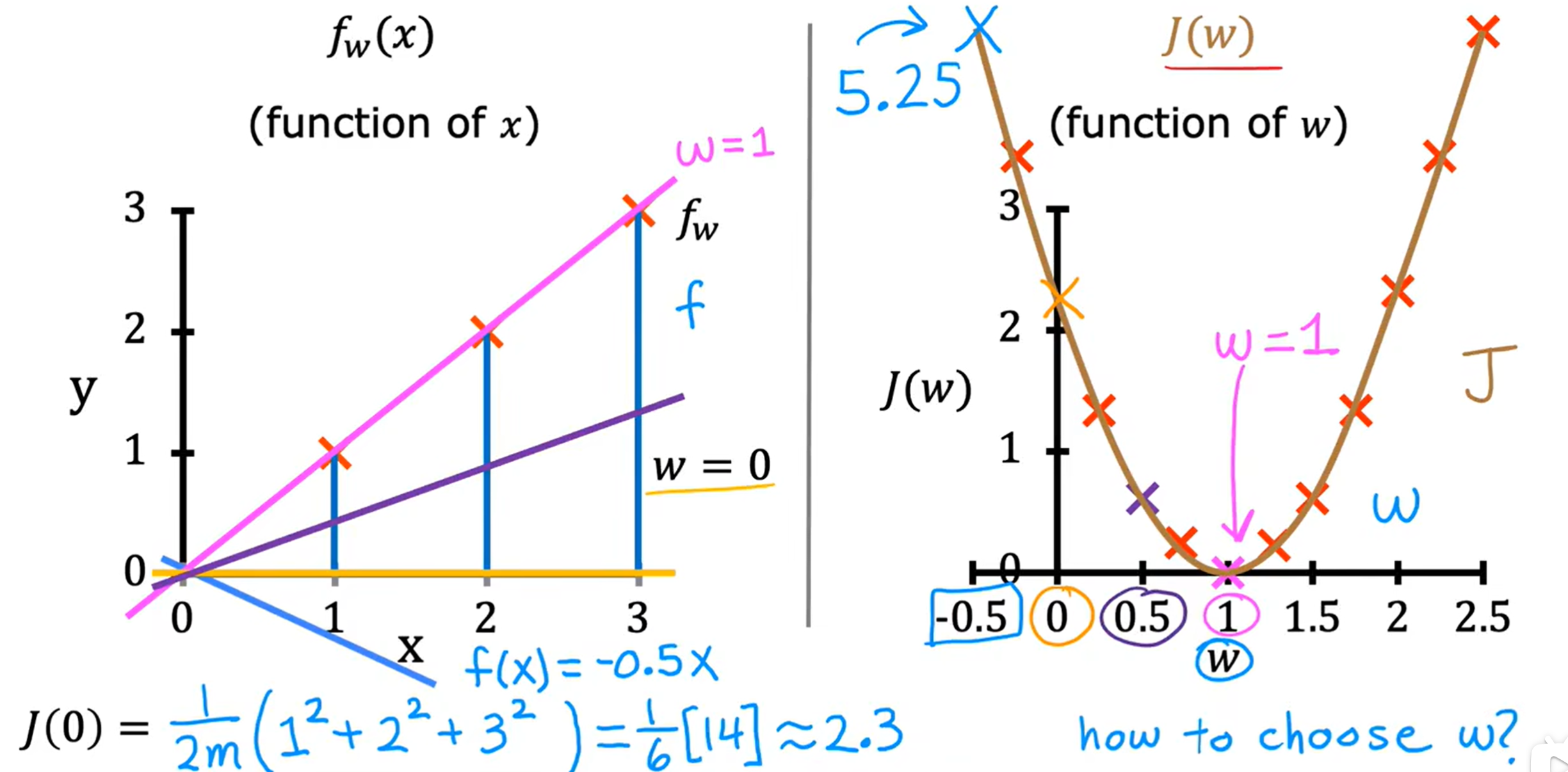
令b = 0，此时函数f(x)=wx，J(w,b) = J(w)，左图绘制了的随着w的变化，函数f(x)的不同图像，右图函数J(w)是关于w的函数，表达式为，当我们分别取w = -0.5，0，0.5，1时，J(a) 分别取值5.25，2.33，0.58，0

由于我们的目标是让该函数值变小，通过不同的取值后绘图，可得J(a)的图像，通过观察我们可以得出，当且仅当w = 1时，J(w)有最小值0，此时模型的预测最接近真实值，拟合度最高。

当b不为零时，对于J(w,b)函数，它有两个变量w和b，此时J(w,b)的图像将呈现三维化（可以理解为先确定一个参量，绘制其图像后再沿着另一个参量的取值范围做积分，无限条线连接成为一个面），如下图所示。

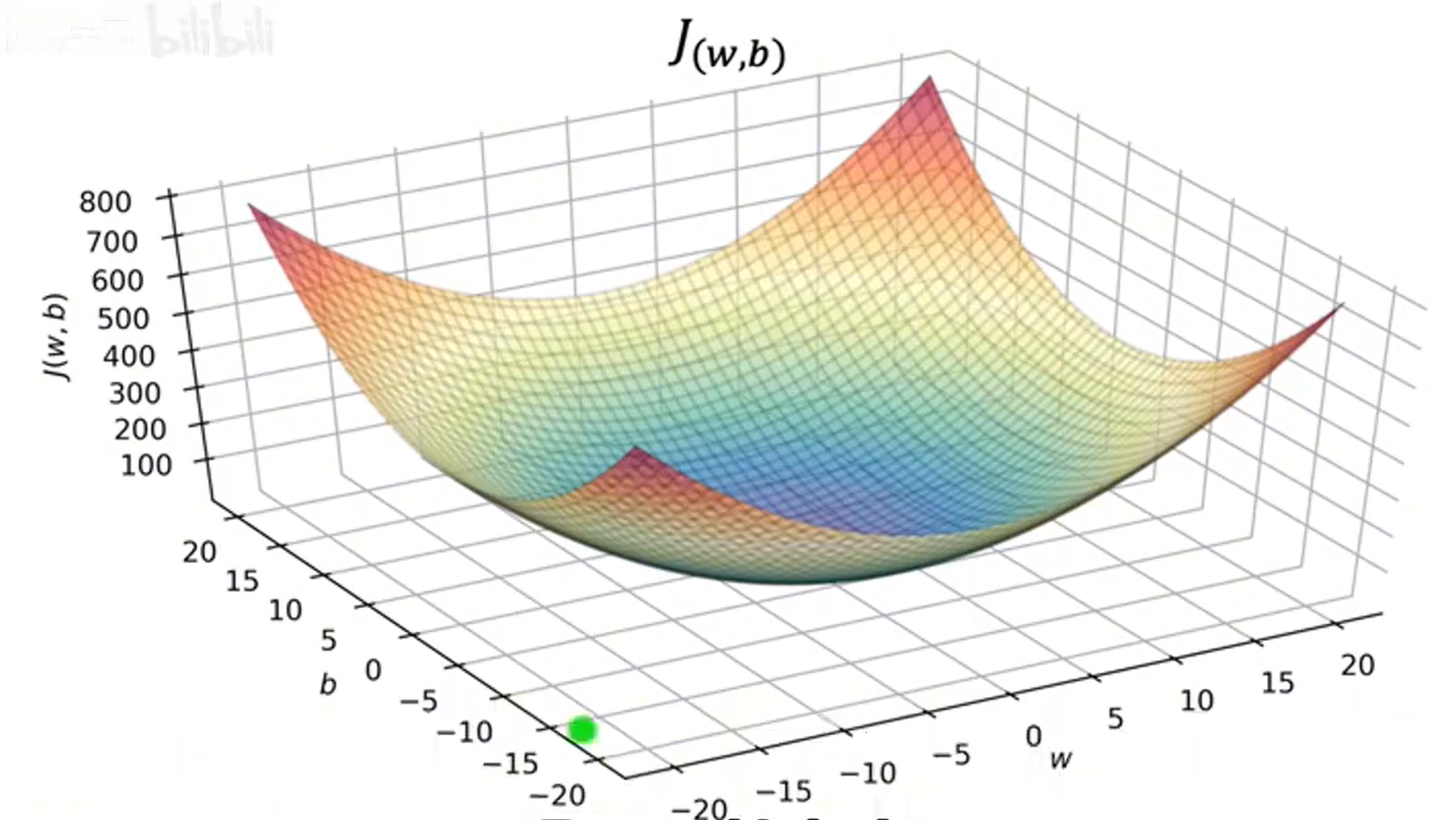
如果使用等高线图来进行图像分析，如下图

坐标系1中的三根颜色的线分别代表不同的拟合函数，坐标系2每个椭圆形的线代表了一个等高线，在该椭圆上的任意一点的值都相同，最小的椭圆的中心代表了等高线的极值，配合坐标系3可以确认其为J(w,b)的最小值，该点的a和b的参数值可以通过坐标系2得出，同时这两个参数所确定的也是拟合效果最好的一条直线，此时模型的预测最接近真实值。如下图。

尽管这样可以非常直观的显示J(w,b)的图像，以及可以很方便地找出最合适的参数w和b，但是当函数f(x)变得复杂，参数变多时(大于两个时），我们必须使用梯度下降算法，编写代码帮助我们找出最合适的参数。

2025.4.23

三、梯度下降（gradient descent）

梯度下降的定义：通过计算代价函数相对于模型参数的梯度，沿着梯度的反方向调整参数，使得代价函数的值逐步减小，再通过不断迭代，最终找到使代价函数最小的参数。

梯度下降算法的示例：

从起点开始，选择一个方向然后每次我们都选择向下变化率最大的方向，向下走，然后重新计算向下变化率最大的方向，一直走到一个谷底处。

从图中我们也能看出有两条路径都到达了各自的谷底处，这两个谷底都为局部极小值。所以通常来说，梯度下降算法会计算出局部最优解（不一定的全局最优解）。

梯度下降算法的数学定义：

承接之前的函数f(x)令参数w和b为（梯度下降的更新公式）：

α为学习率（通常情况下0<α<1，且α默认为0.01)，它在山谷例子中的体现为控制每次下坡时的步幅，过小的α会让步幅变得很小，增加了需要计算的次数；过大的α会让步幅变得很大，无法精确的到达最低点，造成过拟合现象（即参数在更新时来回摆动，无法逐渐逼近局部最小值）。

α决定步幅，偏导数和决定下山的方向（每次都是对上一个J(w,b)求偏导数）

学习率α控制了每次参数更新的速度。当学习率过大（如大于1）会导致参数更新过度，每次步长过大，导致代价函数波动，无法收敛。而学习率过小则会导致训练过程过于缓慢，可能需要很长时间才能看到显著的收敛效果。

正确的计算方法：

按照上述四个公式的顺序进行计算或者编写代码，然后反复进行迭代重复计算。

这里简单补充一下梯度的相关知识点：

        梯度（Gradient）是一个向量，表示了一个多维函数在某一点上各个方向上变化的速率和方向。假设我们有一个多变量函数梯度是该函数关于所有输入变量的偏导数组成的一个向量，记作：

其中:

         是函数关于变量的偏导数，表示在方向上，函数值的变化速率。

梯度是一个多维向量，表示函数在每个方向上的变化速率。

梯度方向是损失函数变化最快的方向，梯度大小表示变化的速度。

零梯度：如果在某个点的梯度为零，表示该点是驻点，可能是局部最小值、局部最大值或者鞍点。需要进一步的检查来确定。

梯度爆炸：梯度在反向传播（从输出到输入，计算每个参数点的梯度，并根据这些梯度值更新模型参数）时迅速增大，导致权重更新过大，模型不稳定。

梯度消失：梯度在反向传播时变得非常小，导致权重更新非常缓慢，模型难以学习。

具体示例：

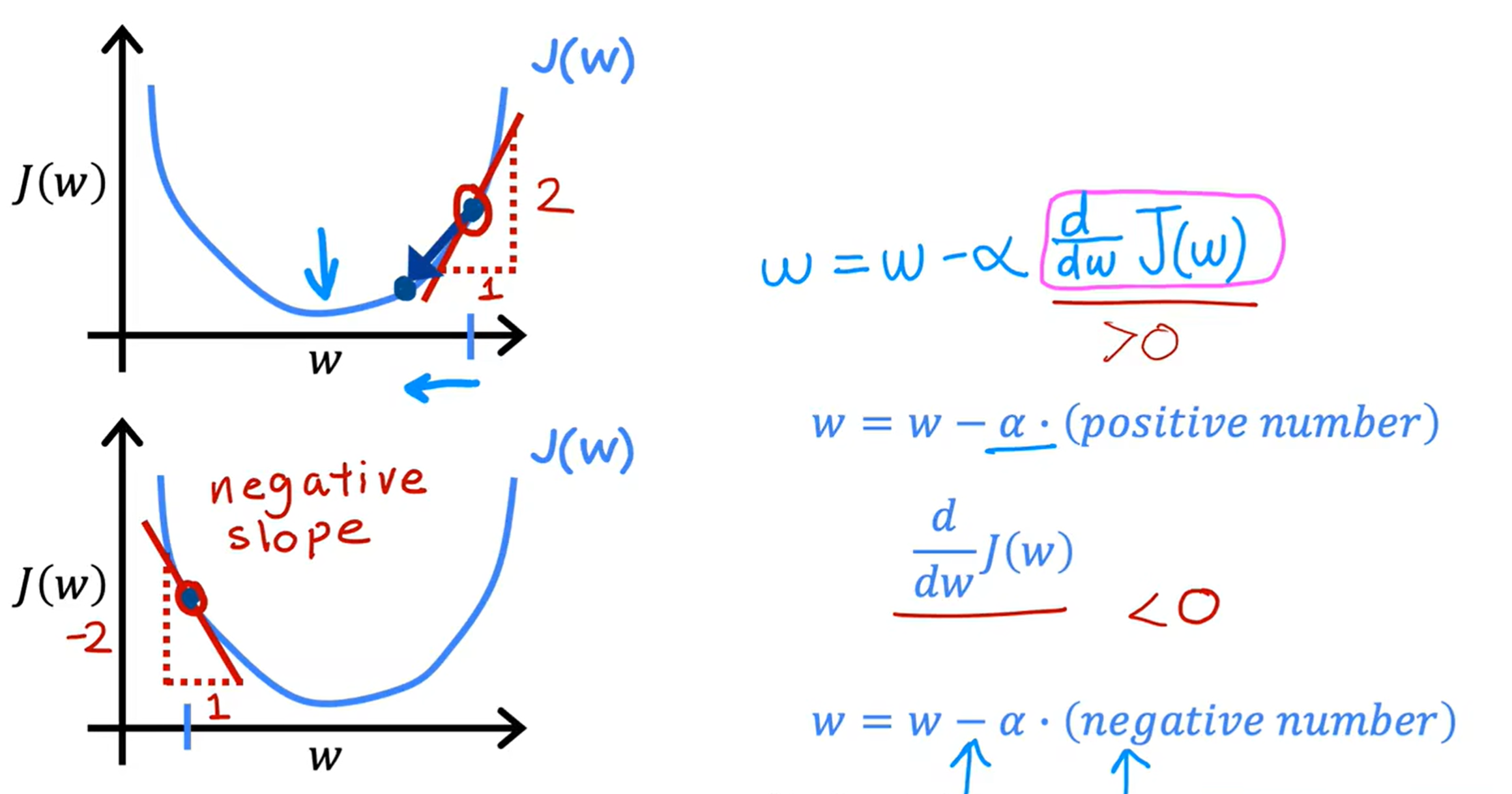
假设b = 0，则J(w)如上图所示，表示在该点处的导数也就是函数J(w)在该点处的斜率，当导数（斜率）大于0时，w减去学习率（正数）乘以斜率，w的值将会越来越小；相反当导数（斜率）小于0时，w减去学习率（正数）乘以斜率，w的值将会越来越大。当学习率固定时，通过不断迭代，w越来越接近局部最小值，斜率也会越来越小，使步幅（w的改变量）越来越小。

局部最小值问题：

若代价函数比较复杂有多个极值时，我们在进行梯度下降算法时会遇到局部最小值（极小值和最小值的比较）问题，即梯度下降算法以及找到了斜率为0点，参数不再变化，但是此点不一定整个函数的最小值，并不完全符合我们的目标。

通过动态调整学习率是一种解决办法，但是需要我们频繁的设置新学习率。因此我们可以使用 ① 动量法 ②模拟退火算法

① 动量法：

动量法源自物理学中的“动量”概念。它通过引入一个“记忆”机制，来加速梯度下降的收敛并减少震荡。动量法的核心思想是，梯度下降不仅仅依赖当前的梯度，还结合了前几次更新的“动量”，从而在更新过程中提供更多的“惯性”，帮助算法跳出局部最优解，保持一个更平稳的优化轨迹。

动量法的更新规则：

在原来的更新规则上，加入动量

其中，是更新的动量，β 是动量的衰减因子（通常取0.9），α是学习率。

对比原来的梯度下降算法：

        加速收敛：通过引入动量，动量法能够在梯度方向上的更新加速收敛，尤其是在面对平坦的区域时，动量有助于加速通过这些区域。

        减少震荡：在训练过程中，梯度下降可能会在陡峭的方向上震荡（例如，在鞍点附近），而动量法通过加权前几次的梯度，能够减少这种震荡，保持平滑的更新轨迹。

        跳出局部最优解：可以帮助跳出局部最优解，因为它在梯度较小的区域会产生较大的更新，从而跳出局部极小值点。

下降过快：由于动量是不断累积的，动量法可能导致收敛速度过快，反而不容易找出最小值。

②模拟退火算法：

模拟退火通过控制一个“温度”参数来调整搜索的行为。首先我们要选择一个较高的温度（通常为常数），并初始化解。然后不断迭代，生成一个新的解，并计算其目标函数值。如果新的解优于当前解，直接接受新的解。如果新的解劣于当前解，仍然有一定概率接受该解，这个概率与当前温度有关。温度越高，接受劣解的概率越大；温度越低，接受劣解的概率越小。

概率值计算方法：

通常采用Metropolis准则来计算：

是新解的目标函数值，是当前解的目标函数值，T 是当前的温度。当计算出后，如果<0，接受新解；>0，则以一定概率 P接受新解。当满足停止条件（如温度过低或达到最大迭代次数），停止算法并返回当前解。

对比原来的梯度下降算法：

        全局搜索能力强：模拟退火通过接受劣解跳出局部最优解，它不再只局限于函数的导数，而是从函数值出发，进行比较运算，从而可以跳出局部最小值。

        避免陷入局部最优解：当搜索空间非常大或者损失函数不规则时，函数可能会有较多的极小值，相比于传统的梯度下降，模拟退火更容易逃脱局部最优解。

        计算成本较高：因为需要在每一轮温度下降过程中计算多个候选解，同时还要指定好初始温度、降温速率等参数，如果函数模型非常复杂，这无疑会增加非常多的计算成本。

2025.4.24

具体计算：