如果你也喜欢C#开发或者.NET开发,可以关注我,我会一直更新相关内容,并且会是超级详细的教程,只要你有耐心,基本上不会有什么问题,如果有不懂的,也可以私信我加我联系方式,我将毫无保留的将我的经验和技术分享给你,不为其他,只为有更多的人进度代码的世界,而进入代码的世界,最快捷和最容易的就是C#.NET,准备好了,就随我加入代码的世界吧!
一、算法简介
期望最大化算法(Expectation-Maximization algorithm,简称EM算法)是一种迭代优化算法,用于在给定隐变量的情况下,估计模型参数的最大似然估计。
EM算法的基本思想是通过迭代的方式,不断地求解两个步骤:E步和M步。在E步中,根据当前的参数估计值,计算隐变量的期望值;在M步中,根据E步计算得到的隐变量的期望值,求解出新的参数估计值。不断重复这两个步骤,直到参数收敛为止。
具体来说,假设我们要估计一个包含隐变量的概率模型参数θ。首先,给定当前的参数估计值θ(t),在E步中计算隐变量的期望值Q(θ|θ(t))。然后,在M步中求解出新的参数估计值θ(t+1),使得似然函数L(θ)在给定隐变量的期望值下达到最大值。重复执行这两个步骤,直到参数收敛。
EM算法的优点是可以应用于包含隐变量的概率模型参数估计,并且能够在缺少观测值的情况下进行估计。它的缺点是对初始参数的选择比较敏感,并且只能达到局部最优。
二、为什么要学习期望最大化算法
2.1 参数估计
EM算法是一种用于参数估计的有效方法。在许多概率模型中,参数估计是一个重要的任务,通过学习EM算法,可以有效地估计出模型中的参数。
2.2 缺失数据处理
在许多真实世界的问题中,数据集中可能存在缺失数据。EM算法可以通过填补或估计缺失数据来提高数据集的完整性和准确性。
2.3 聚类分析
EM算法可以用于聚类分析,即将数据集分成不同的组或类。通过学习EM算法,可以将数据按照概率模型中的分布特征进行划分,从而得到更好的聚类结果。
2.4 高斯混合模型
EM算法在高斯混合模型中的应用非常广泛。高斯混合模型是一种常用的概率模型,可以用于聚类、分类和异常检测等任务。学习EM算法有助于理解和应用高斯混合模型。
三、期望最大化算法在项目中有哪些实际应用
3.1 推荐系统
利用期望最大化算法,可以根据用户的历史行为和偏好,推荐最可能满足用户需求的商品或内容,提高用户满意度和转化率。
3.2 机器学习
期望最大化算法在概率图模型中被广泛应用,如隐马尔可夫模型、概率主题模型等,用于参数估计和潜在变量的推断。
3.3 聚类分析
期望最大化算法可以用于聚类分析,将数据集划分成具有相似特征的群组,有助于发现数据的内在结构和规律。
3.4 强化学习
期望最大化算法在强化学习中用于求解马尔可夫决策过程(MDP),通过最大化累积奖励,找到最优的决策策略。
3.5 金融风险管理
期望最大化算法可以用于模型参数估计和风险度量,帮助金融机构更准确地评估风险和制定风险控制策略。
3.6 医疗诊断
期望最大化算法可以用于潜在类别模型,对医疗诊断中的潜在疾病进行推断和分类,辅助医生做出准确的诊断决策。
3.7 图像处理
期望最大化算法可以用于图像分割和图像生成,将图像分割成不同的区域或生成新的图像,有助于图像分析和图像编辑等应用。
3.8 自然语言处理
期望最大化算法可以用于模型参数估计和文本生成,例如在语言模型中,通过最大化语句的生成概率,生成符合语法和语义规则的文本。
3.9 数据挖掘
期望最大化算法可以用于挖掘数据中的潜在模式和关联规则,发现数据中隐藏的信息和规律,帮助企业做出更准确的决策。
3.10 其他领域
期望最大化算法还可以在信号处理、网络优化、市场营销等领域中应用,提高系统性能和决策效果。
四、期望最大化算法的实现与讲解
4.1 算法实现
实现
class GaussianMixtureModel
{
public double[] data; // 数据样本
public int k; // 高斯分布的数量
public double[] means; // 各个高斯分布的均值
public double[] variances; // 各个高斯分布的方差
public double[] weights; // 各个高斯分布的权重
public GaussianMixtureModel(double[] data, int k)
{
this.data = data;
this.k = k;
this.means = new double[k];
this.variances = new double[k];
this.weights = new double[k];
}
public void Train(int iterations)
{
// 随机初始化参数
InitParameters();
for (int iteration = 0; iteration < iterations; iteration++)
{
// E步:计算后验概率
double[,] posteriorProbabilities = Expectation();
// M步:更新参数
Maximization(posteriorProbabilities);
}
}
private void InitParameters()
{
Random random = new Random();
// 随机分配权重
double sum = 0;
for (int i = 0; i < k; i++)
{
weights[i] = random.NextDouble();
sum += weights[i];
}
for (int i = 0; i < k; i++)
{
weights[i] /= sum;
}
// 随机分配均值和方差
for (int i = 0; i < k; i++)
{
means[i] = random.NextDouble() * data.Length;
variances[i] = random.NextDouble();
}
}
private double[,] Expectation()
{
double[,] posteriorProbabilities = new double[data.Length, k];
for (int i = 0; i < data.Length; i++)
{
double sum = 0;
// 计算每个高斯分布下的后验概率
for (int j = 0; j < k; j++)
{
posteriorProbabilities[i, j] = weights[j] * Gaussian(data[i], means[j], variances[j]);
sum += posteriorProbabilities[i, j];
}
// 归一化后验概率
for (int j = 0; j < k; j++)
{
posteriorProbabilities[i, j] /= sum;
}
}
return posteriorProbabilities;
}
private void Maximization(double[,] posteriorProbabilities)
{
double[] sumWeights = new double[k];
double[] sumMeans = new double[k];
double[] sumVariances = new double[k];
// 计算每个高斯分布的累积和
for (int i = 0; i < data.Length; i++)
{
for (int j = 0; j < k; j++)
{
sumWeights[j] += posteriorProbabilities[i, j];
sumMeans[j] += posteriorProbabilities[i, j] * data[i];
sumVariances[j] += posteriorProbabilities[i, j] * Math.Pow(data[i] - means[j], 2);
}
}
// 更新参数
for (int j = 0; j < k; j++)
{
weights[j] = sumWeights[j] / data.Length;
means[j] = sumMeans[j] / sumWeights[j];
variances[j] = sumVariances[j] / sumWeights[j];
}
}
private double Gaussian(double x, double mean, double variance)
{
double exponent = -0.5 * Math.Pow(x - mean, 2) / variance;
double coefficient = 1 / Math.Sqrt(2 * Math.PI * variance);
return coefficient * Math.Exp(exponent);
}
}调用
public static void Main(string[] args)
{
double[] data = { 1.2, 1.5, 2.0, 3.5, 4.0, 4.2, 5.0, 6.5, 6.8, 7.0 };
int k = 2;
GaussianMixtureModel model = new GaussianMixtureModel(data, k);
model.Train(iterations: 1000);
for (int i = 0; i < k; i++)
{
Console.WriteLine("高斯模型 {0}\t权重={1}\t均值={2}\t方差={3}",i, model.weights[i], model.means[i], model.variances[i]);
}
}输出结果
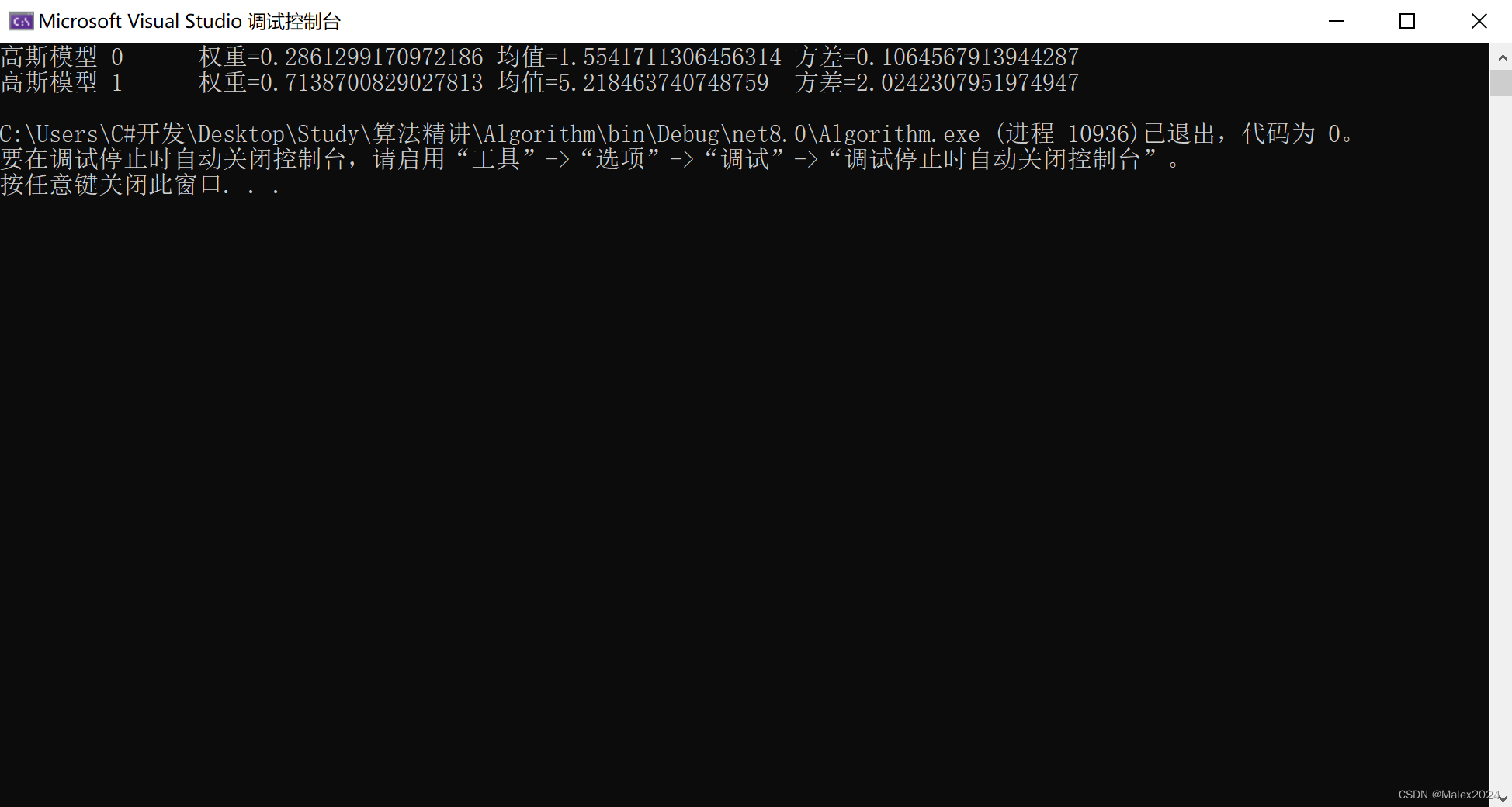
4.2 算法讲解
上述代码实现了高斯混合模型的期望最大化算法,下面逐步解释代码的功能:
-
首先定义了一个
GaussianMixtureModel类,表示高斯混合模型。它包含了一些私有字段用于存储模型的参数,如数据样本(data)、高斯分布的数量(k)、各个高斯分布的均值(means)、方差(variances)和权重(weights)。 -
GaussianMixtureModel类的构造函数接收数据样本和高斯分布的数量,并初始化参数数组。 -
Train方法是训练模型的核心方法。它根据迭代次数(iterations)执行期望最大化算法的迭代过程。 -
在
InitParameters方法中,模型的参数被随机初始化。权重数组(weights)被随机赋值,并归一化使其总和为1。均值数组(means)被随机赋值在样本长度范围内,方差数组(variances)被随机赋值。 -
在每次迭代中,算法先执行E步骤,计算每个数据样本属于每个高斯分布的后验概率。在
Expectation方法中,一个双层循环遍历每个样本和每个高斯分布,使用高斯分布的权重和高斯函数来计算后验概率。然后将后验概率归一化,以确保它们的总和为1。最后,返回一个二维数组(posteriorProbabilities),存储每个样本属于每个高斯分布的后验概率。 -
接下来执行M步骤,更新高斯分布的参数。在
Maximization方法中,先声明一些临时的累积和数组,用于计算新的参数值。使用嵌套循环遍历每个样本和每个高斯分布,根据后验概率更新累积和数组的值。最后,根据累积和数组的值计算新的高斯分布的参数,并更新模型的参数数组。 -
Gaussian方法用于计算给定值(x)在给定均值(mean)和方差(variance)下的高斯概率密度函数的值。 -
Main方法是程序的入口。定义了一个示例数据数组(data)和高斯分布的数量(k)。创建一个GaussianMixtureModel对象,并调用Train方法进行训练。最后,打印输出估计的高斯分布的参数。
五、期望最大化算法需要注意的地方
5.1 初始参数的选择
期望最大化算法对初始参数非常敏感。不同的初始参数可能导致不同的局部最优解或者算法的不收敛。因此,选择合适的初始参数非常重要,可以利用先验知识、随机采样或其他启发式方法来选择初始参数。
5.2 收敛条件的设定
期望最大化算法需要一个收敛条件来判断算法是否收敛。常见的收敛条件可以有两种:一种是设定一个最大迭代次数,如果迭代次数达到最大值仍然没有收敛,则停止迭代;另一种是设定一个误差阈值,如果两次迭代之间的参数变化小于误差阈值,则停止迭代。选择合适的收敛条件可以保证算法在合理的时间内收敛。
5.3 数据预处理
期望最大化算法对输入数据的分布形状和尺度非常敏感。如果输入数据有不同的分布形状和尺度,可能导致算法收敛到不合理的结果。因此,在使用期望最大化算法之前,需要对输入数据进行归一化、标准化或其他预处理操作,使得数据具有相似的分布形状和尺度。
5.4 解空间的局部最优解
期望最大化算法是一种贪心算法,它在每一次迭代中都选择局部最优解。由于解空间通常非常复杂,可能存在多个局部最优解。因此,期望最大化算法不能保证找到全局最优解。为了避免陷入局部最优解,可以通过多次运行算法并选择最优解的方式来提高算法的性能。
5.5 模型选择和参数调优
期望最大化算法通常用于估计模型的参数。在使用期望最大化算法之前,需要根据实际问题选择合适的模型,并调优模型的参数。合适的模型和参数选择可以提高算法的性能和收敛速度。






















 692
692

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








