本文承接上篇上篇在此和中篇中篇在此,继续就Sepp Hochreiter 1997年的开山大作 Long Short-term Memory 中APPENDIX A.1和A.2所载的数学推导过程进行详细解读。希望可以帮助大家理解了这个推导过程,进而能顺利理解为什么那几个门的设置可以解决RNN里的梯度消失和梯度爆炸的问题。中篇介绍了各个权重的误差更新算法。本篇将继续说明梯度信息在LSTM的记忆单元中经过一定的时间步之后如何变化,并由此证明LSTM可实现CEC(Constant Error Carousel)。本篇为整个文章的终章,也是最关键的一篇,因为此篇正是理解LSTM实现CEC的关键。一家之言,若有任何错漏欢迎大家评论区指正。好了,Dig in!
6. 误差流
我们将计算误差值在记忆单元上流过 q q q时间步之后(也称误差流error flow)的变化情况。
6.1 记忆单元输出点的误差值计算
已知记忆单元的计算公式:
s
c
j
(
t
)
=
s
c
j
(
t
−
1
)
+
g
(
n
e
t
c
j
(
t
)
)
y
i
n
j
(
t
)
s_{c_j}(t) = s_{c_j}(t-1) + g(net_{c_j}(t)) y^{in_j}(t)
scj(t)=scj(t−1)+g(netcj(t))yinj(t)
我们使用截断求导规则来计算误差在时间步
t
−
k
t-k
t−k和
t
−
k
−
1
t-k-1
t−k−1之间的变化情况:
∂
s
c
j
(
t
−
k
)
∂
s
c
j
(
t
−
k
−
1
)
=
1
+
∂
g
(
n
e
t
c
j
(
t
−
k
)
)
y
i
n
j
(
t
−
k
)
∂
s
c
j
(
t
−
k
−
1
)
=
1
+
∂
y
i
n
j
(
t
−
k
)
∂
s
c
j
(
t
−
k
−
1
)
g
(
n
e
t
c
j
(
t
−
k
)
)
+
∂
g
(
n
e
t
c
j
(
t
−
k
)
)
∂
s
c
j
(
t
−
k
−
1
)
y
i
n
j
(
t
−
k
)
=
1
+
∑
u
[
∂
y
i
n
j
(
t
−
k
)
∂
y
u
(
t
−
k
−
1
)
∂
y
u
(
t
−
k
−
1
)
∂
s
c
j
(
t
−
k
−
1
)
]
g
(
n
e
t
c
j
(
t
−
k
)
)
+
y
i
n
j
(
t
−
k
)
g
′
(
n
e
t
c
j
(
t
−
k
)
)
∑
u
[
∂
n
e
t
c
j
(
t
−
k
)
∂
y
u
(
t
−
k
−
1
)
∂
y
u
(
t
−
k
−
1
)
∂
s
c
j
(
t
−
k
−
1
)
]
≈
t
r
1.
(30)
\begin{aligned} \frac{\partial s_{c_j}(t-k)}{\partial s_{c_j}(t-k-1)} &= 1 + \frac{\partial g(net_{c_j}(t-k))y^{in_j}(t-k)}{\partial s_{c_j}(t-k-1)}\\ &=1+ \frac{\partial y^{in_j}(t-k)}{\partial s_{c_j}(t-k-1)}g(net_{c_j}(t-k)) + \frac{\partial g(net_{c_j}(t-k))}{\partial s_{c_j}(t-k-1)}y^{in_j}(t-k)\\ &=1 + \sum_u[\frac{\partial y^{in_j}(t-k)}{\partial y^u(t-k-1)}\frac{\partial y^u(t-k-1)}{\partial s_{c_j}(t-k-1)}]g(net_{c_j}(t-k)) \\ &\quad + y^{in_j}(t-k)g'(net_{c_j}(t-k))\sum_u [\frac{\partial net_{c_j}(t-k)}{\partial y^u(t-k-1)}\frac{\partial y^u(t-k-1)}{\partial s_{c_j}(t-k-1)}]\\ &\approx_{tr} 1.\tag{30} \end{aligned}
∂scj(t−k−1)∂scj(t−k)=1+∂scj(t−k−1)∂g(netcj(t−k))yinj(t−k)=1+∂scj(t−k−1)∂yinj(t−k)g(netcj(t−k))+∂scj(t−k−1)∂g(netcj(t−k))yinj(t−k)=1+u∑[∂yu(t−k−1)∂yinj(t−k)∂scj(t−k−1)∂yu(t−k−1)]g(netcj(t−k))+yinj(t−k)g′(netcj(t−k))u∑[∂yu(t−k−1)∂netcj(t−k)∂scj(t−k−1)∂yu(t−k−1)]≈tr1.(30)
根据截断求导的规则,上式中的
∂
y
i
n
j
(
t
−
k
)
∂
y
u
(
t
−
k
−
1
)
\frac{\partial y^{in_j}(t-k)}{\partial y^u(t-k-1)}
∂yu(t−k−1)∂yinj(t−k)和
∂
n
e
t
c
j
(
t
−
k
)
∂
y
u
(
t
−
k
−
1
)
\frac{\partial net_{c_j}(t-k)}{\partial y^u(t-k-1)}
∂yu(t−k−1)∂netcj(t−k)都等于0。因此上式应用截断求导规则之后,最终结果等于1。上边这个式子有两个累加符号
∑
u
\sum_u
∑u可能会让人感到迷惑,按照我们一般的理解,应用链式求导规则,
∂
y
i
n
j
(
t
−
k
)
∂
s
c
j
(
t
−
k
−
1
)
=
∂
y
i
n
j
(
t
−
k
)
∂
y
u
(
t
−
k
−
1
)
∂
y
u
(
t
−
k
−
1
)
∂
s
c
j
(
t
−
k
−
1
)
,
\frac{\partial y^{in_j}(t-k)}{\partial s_{c_j}(t-k-1)}=\frac{\partial y^{in_j}(t-k)}{\partial y^u(t-k-1)}\frac{\partial y^u(t-k-1)}{\partial s_{c_j}(t-k-1)},
∂scj(t−k−1)∂yinj(t−k)=∂yu(t−k−1)∂yinj(t−k)∂scj(t−k−1)∂yu(t−k−1),为什么这里是
∂
y
i
n
j
(
t
−
k
)
∂
s
c
j
(
t
−
k
−
1
)
=
∑
u
[
∂
y
i
n
j
(
t
−
k
)
∂
y
u
(
t
−
k
−
1
)
∂
y
u
(
t
−
k
−
1
)
∂
s
c
j
(
t
−
k
−
1
)
]
.
\frac{\partial y^{in_j}(t-k)}{\partial s_{c_j}(t-k-1)}=\sum_u[\frac{\partial y^{in_j}(t-k)}{\partial y^u(t-k-1)}\frac{\partial y^u(t-k-1)}{\partial s_{c_j}(t-k-1)}].
∂scj(t−k−1)∂yinj(t−k)=u∑[∂yu(t−k−1)∂yinj(t−k)∂scj(t−k−1)∂yu(t−k−1)].
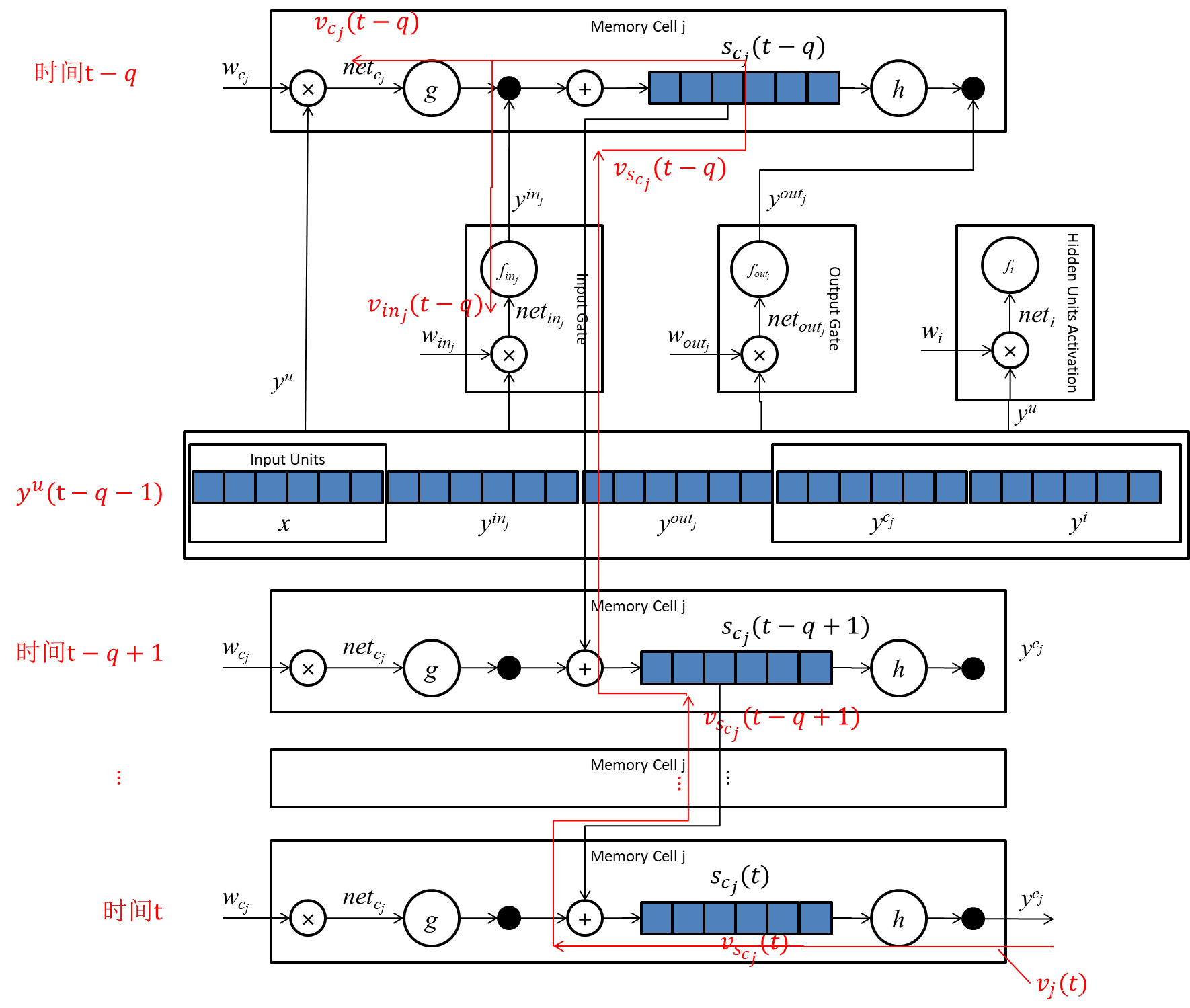
为了解释这个情况,我们需要先看一下下边从 y i n j ( t − k ) y^{in_j}(t-k) yinj(t−k)到 s c j ( t − k − 1 ) s_{c_j}(t-k-1) scj(t−k−1)的误差传播路径示意图:
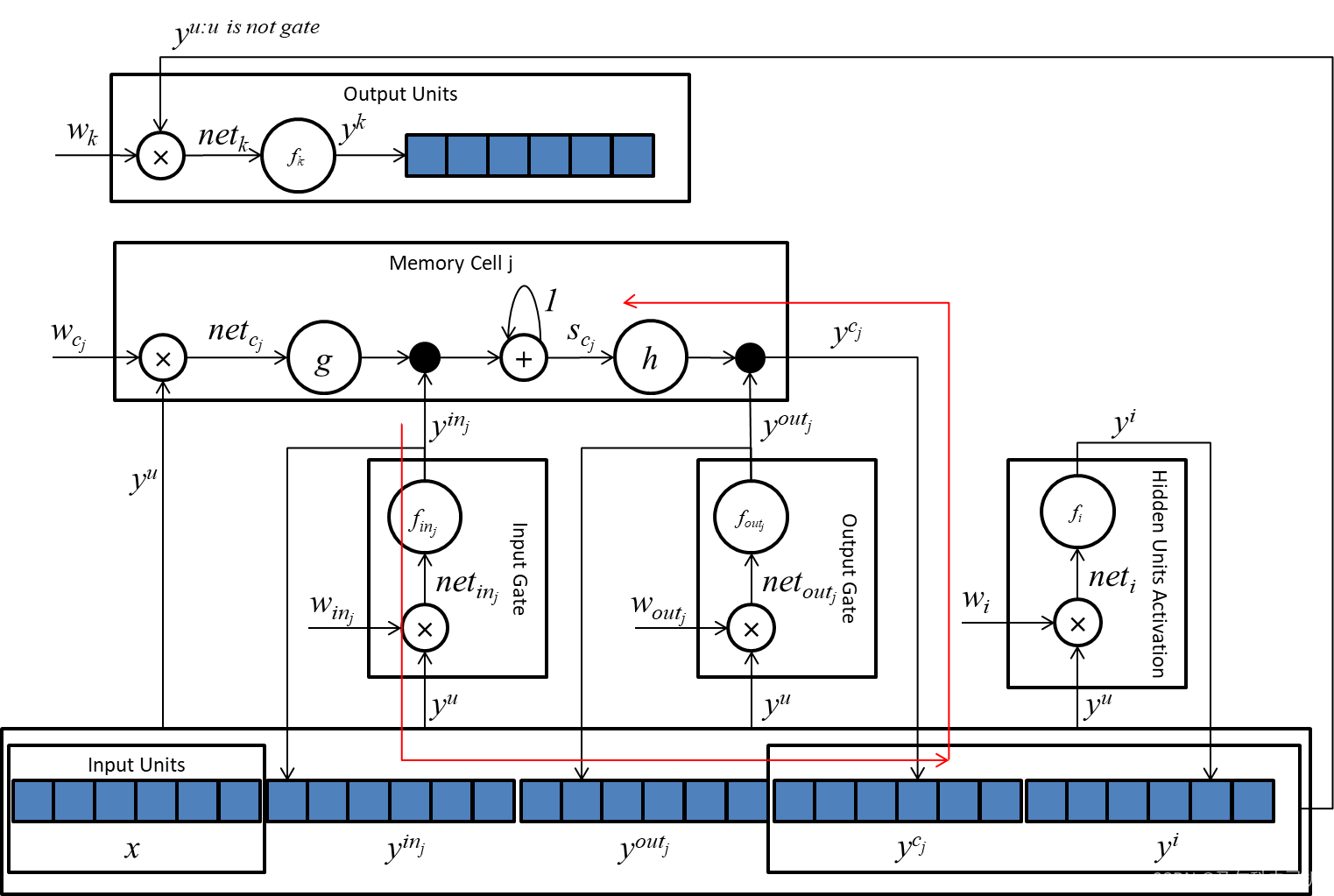
我们把传播路径上的各个节点展开一下(如下图所示),这里边
y
i
n
j
(
t
−
k
)
y^{in_j}(t-k)
yinj(t−k)和
s
c
j
(
t
−
k
−
1
)
s_{c_j}(t-k-1)
scj(t−k−1)所属的向量长度是一样的,
y
u
(
t
−
k
−
1
)
y^u(t-k-1)
yu(t−k−1)所属向量的长度与其他两个不同。
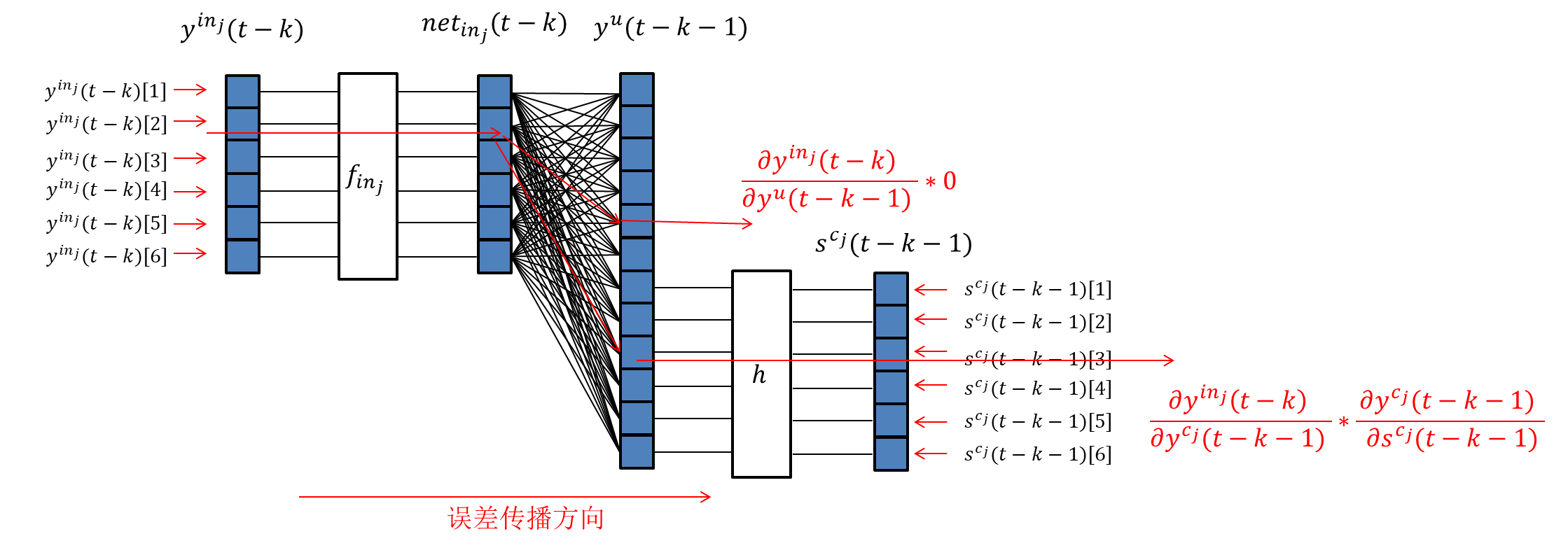
上图分别显示了
∂
y
i
n
j
(
t
−
k
)
∂
y
u
(
t
−
k
−
1
)
\frac{\partial y^{in_j}(t-k)}{\partial y^u(t-k-1)}
∂yu(t−k−1)∂yinj(t−k)及
∂
y
u
(
t
−
k
−
1
)
∂
s
c
j
(
t
−
k
−
1
)
\frac{\partial y^u(t-k-1)}{\partial s_{c_j}(t-k-1)}
∂scj(t−k−1)∂yu(t−k−1)的现实含义。从上图可以看出,在给定
c
j
c_j
cj和
i
n
j
in_j
inj值的情况下,由于大部分的
y
u
(
t
−
k
−
1
)
y^u(t-k-1)
yu(t−k−1)的单元和
s
c
j
s_{c_j}
scj节点连接。因此当且仅当
u
=
c
j
u=c_j
u=cj时,
∂
y
i
n
j
(
t
−
k
)
∂
y
u
(
t
−
k
−
1
)
∂
y
u
(
t
−
k
−
1
)
∂
s
c
j
(
t
−
k
−
1
)
≠
0
\frac{\partial y^{in_j}(t-k)}{\partial y^u(t-k-1)}\frac{\partial y^u(t-k-1)}{\partial s_{c_j}(t-k-1)} \ne 0
∂yu(t−k−1)∂yinj(t−k)∂scj(t−k−1)∂yu(t−k−1)=0。所以我们有:
∑
u
[
∂
y
i
n
j
(
t
−
k
)
∂
y
u
(
t
−
k
−
1
)
∂
y
u
(
t
−
k
−
1
)
∂
s
c
j
(
t
−
k
−
1
)
]
=
∂
y
i
n
j
(
t
−
k
)
∂
y
c
j
(
t
−
k
−
1
)
∂
y
c
j
(
t
−
k
−
1
)
∂
s
c
j
(
t
−
k
−
1
)
\sum_u[\frac{\partial y^{in_j}(t-k)}{\partial y^u(t-k-1)}\frac{\partial y^u(t-k-1)}{\partial s_{c_j}(t-k-1)}]= \frac{\partial y^{in_j}(t-k)}{\partial y^{c_j}(t-k-1)}\frac{\partial y^{c_j}(t-k-1)}{\partial s_{c_j}(t-k-1)}
u∑[∂yu(t−k−1)∂yinj(t−k)∂scj(t−k−1)∂yu(t−k−1)]=∂ycj(t−k−1)∂yinj(t−k)∂scj(t−k−1)∂ycj(t−k−1)
同理可得:
∑
u
[
∂
n
e
t
c
j
(
t
−
k
)
∂
y
u
(
t
−
k
−
1
)
∂
y
u
(
t
−
k
−
1
)
∂
s
c
j
(
t
−
k
−
1
)
]
=
∂
n
e
t
c
j
(
t
−
k
)
∂
y
c
j
(
t
−
k
−
1
)
∂
y
c
j
(
t
−
k
−
1
)
∂
s
c
j
(
t
−
k
−
1
)
\sum_u [\frac{\partial net_{c_j}(t-k)}{\partial y^u(t-k-1)}\frac{\partial y^u(t-k-1)}{\partial s_{c_j}(t-k-1)}]=\frac{\partial net_{c_j}(t-k)}{\partial y^{c_j}(t-k-1)}\frac{\partial y^{c_j}(t-k-1)}{\partial s_{c_j}(t-k-1)}
u∑[∂yu(t−k−1)∂netcj(t−k)∂scj(t−k−1)∂yu(t−k−1)]=∂ycj(t−k−1)∂netcj(t−k)∂scj(t−k−1)∂ycj(t−k−1)
我们用
v
j
(
t
)
v_j(t)
vj(t)表示
t
t
t时刻从记忆单元输出点的误差信号,
v
i
(
t
)
v_i(t)
vi(t)表示隐藏单元的误差信号,
v
k
(
t
)
v_k(t)
vk(t)表示输出单元的误差信号。如下图所示:
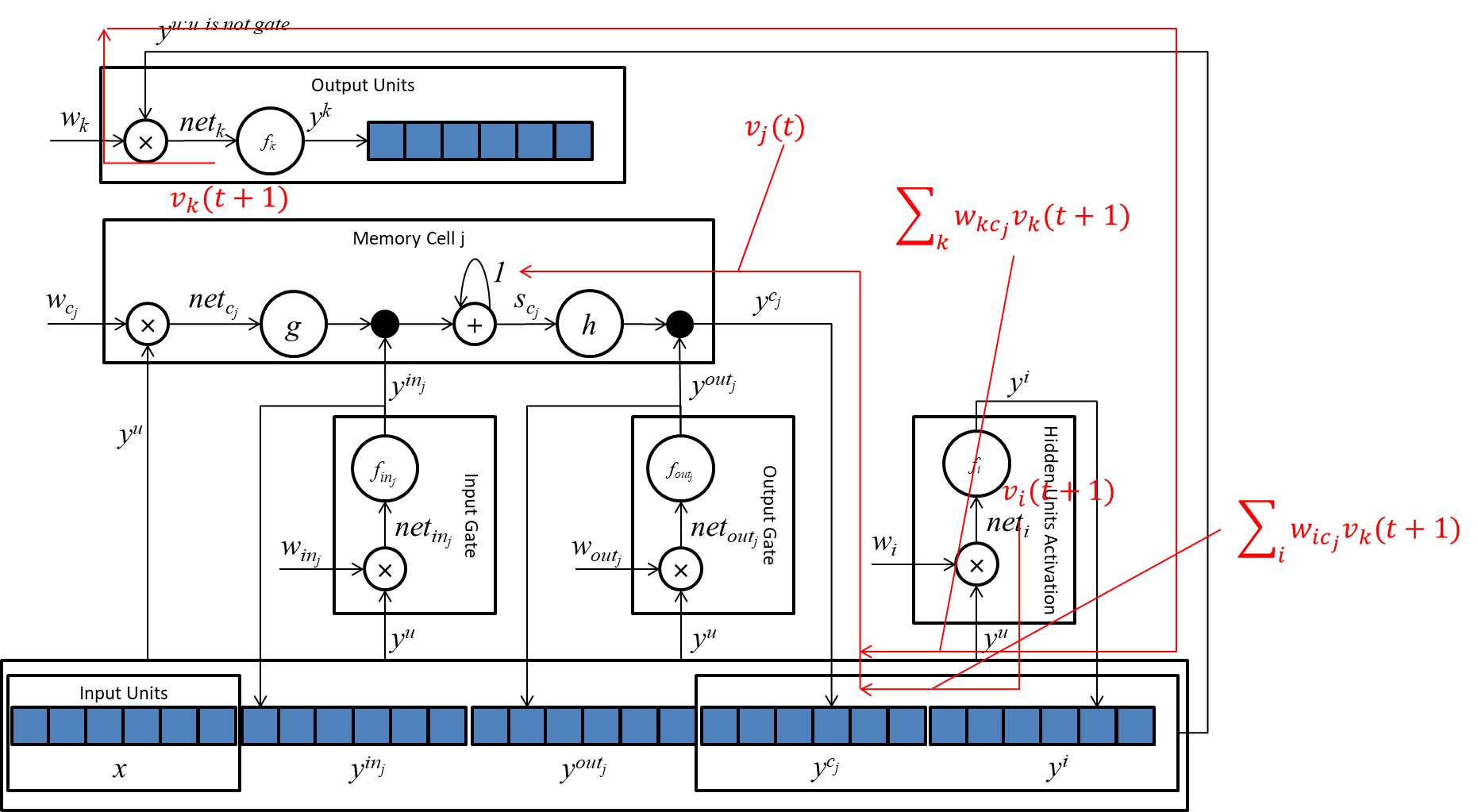
我们可以如此定义
v
j
(
t
)
v_j(t)
vj(t):
v
j
(
t
)
:
=
∑
k
w
k
c
j
v
k
(
t
+
1
)
+
∑
i
w
i
c
j
v
i
(
t
+
1
)
v_j(t):=\sum_kw_{kc_j}v_k(t+1) + \sum_iw_{ic_j}v_i(t+1)
vj(t):=k∑wkcjvk(t+1)+i∑wicjvi(t+1)
原文中采用了一种更加通用的表达方式,即使用
i
:
i
n
o
g
a
t
e
a
n
d
n
o
m
e
m
o
r
y
c
e
l
l
i:\ i\ no\ gate\ and\ no\ memory\ cell
i: i no gate and no memory cell同时代表上式中的
k
,
i
k,i
k,i。我们可以将上式改写为原文中的形式:
v
j
(
t
)
:
=
∑
i
:
i
n
o
g
a
t
e
a
n
d
n
o
m
e
m
o
r
y
c
e
l
l
w
i
c
j
v
i
(
t
+
1
)
.
(31)
v_j(t):=\sum_{i:\ i\ no\ gate\ and\ no\ memory\ cell}w_{ic_j}v_i(t+1)\tag{31}.
vj(t):=i: i no gate and no memory cell∑wicjvi(t+1).(31)
由于这个表示会跟隐藏单元误差信号的标识冲突,所以我们把式31重新写成:
v
j
(
t
)
:
=
∑
u
:
u
n
o
g
a
t
e
a
n
d
n
o
m
e
m
o
r
y
c
e
l
l
w
u
c
j
v
u
(
t
+
1
)
.
(31*)
v_j(t):=\sum_{u:\ u\ no\ gate\ and\ no\ memory\ cell}w_{uc_j}v_u(t+1).\tag{31*}
vj(t):=u: u no gate and no memory cell∑wucjvu(t+1).(31*)
6.2 输出门的误差值计算
此时我们可以计算
t
t
t时刻,输出门得到的误差值
v
o
u
t
j
(
t
)
v_{out_j}(t)
voutj(t),该误差值的设定为处于
n
e
t
o
u
t
j
net_{out_j}
netoutj处,如下图所示:
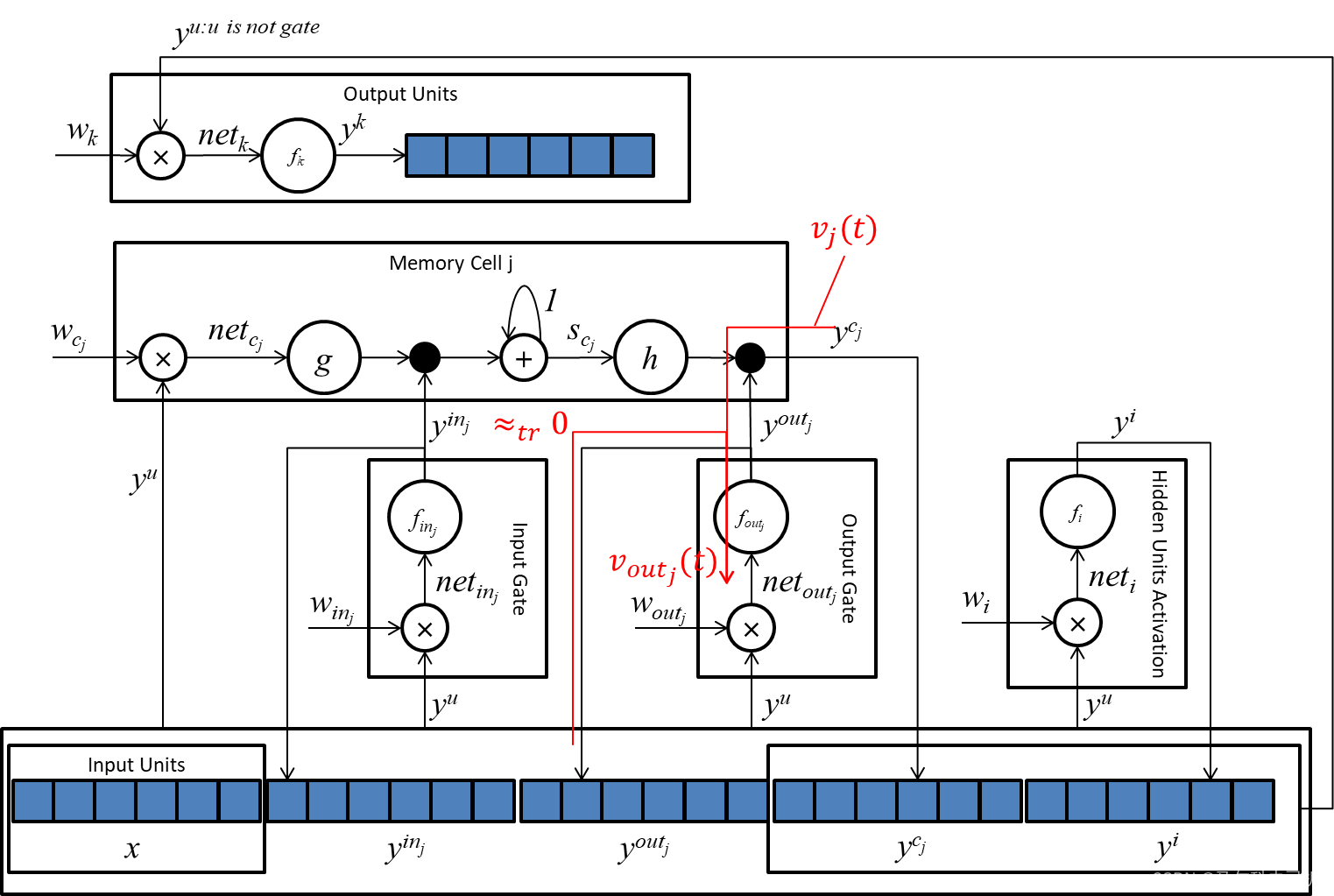
v
o
u
t
j
(
t
)
≈
t
r
∂
y
c
j
(
t
)
∂
n
e
t
o
u
t
j
(
t
)
v
j
(
t
)
≈
t
r
∂
y
c
j
(
t
)
∂
y
o
u
t
j
(
t
)
∂
y
o
u
t
j
(
t
)
∂
n
e
t
o
u
t
j
(
t
)
v
j
(
t
)
.
(32)
\begin{aligned} v_{out_j}(t) &\approx_{tr} \frac{\partial y^{c_j(t)}}{\partial net_{out_j}(t)}v_j(t)\\ &\approx_{tr}\frac{\partial y^{c_j(t)}}{\partial y^{out_j}(t)} \frac{\partial y^{out_j}(t)}{\partial net_{out_j}(t)}v_j(t)\tag{32}. \end{aligned}
voutj(t)≈tr∂netoutj(t)∂ycj(t)vj(t)≈tr∂youtj(t)∂ycj(t)∂netoutj(t)∂youtj(t)vj(t).(32)
6.3 CEC的误差值计算
我们现在来计算在
t
t
t时刻传播到记忆单元内部的
s
c
j
s_{c_j}
scj处的误差值。误差值传播路径示意图:
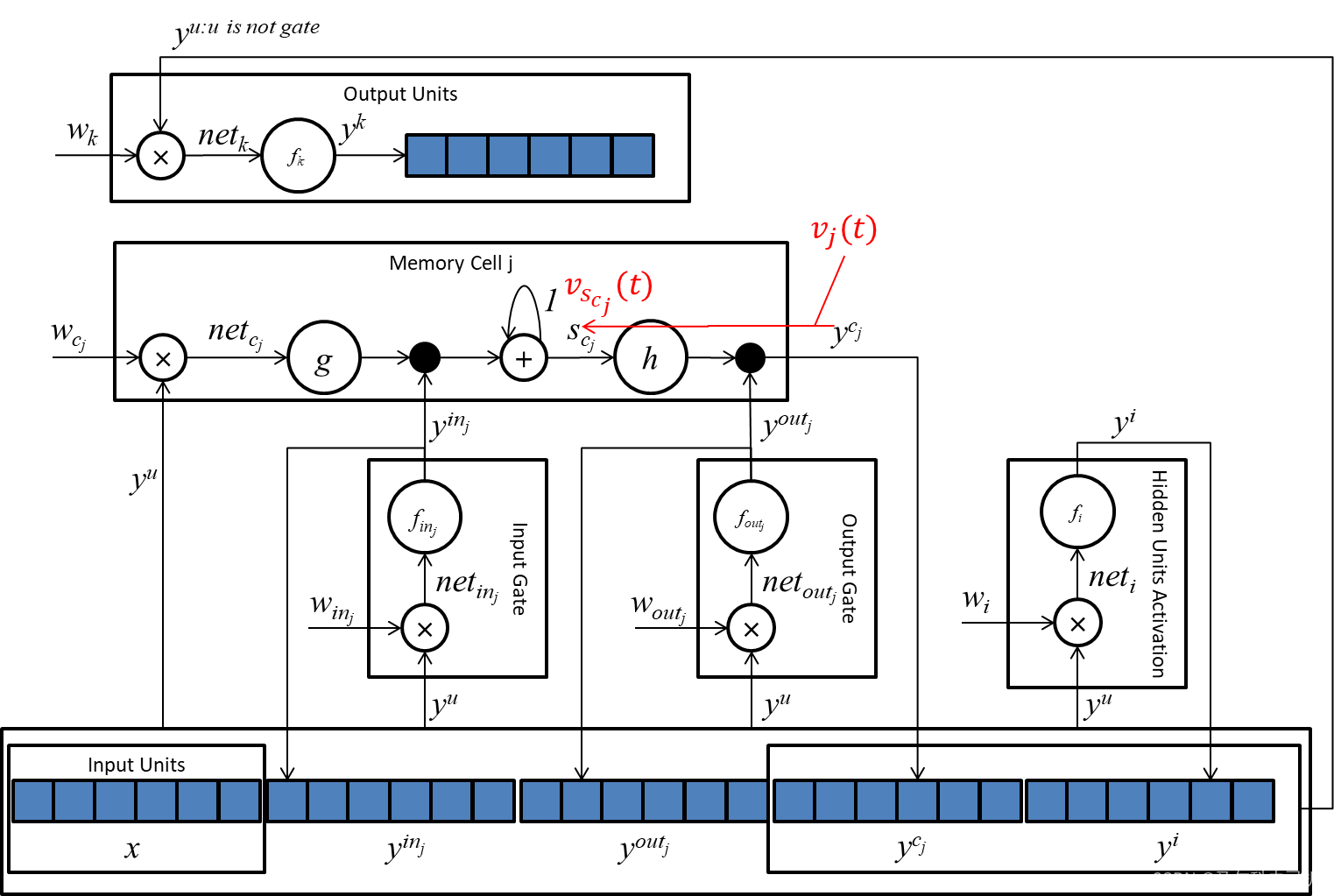
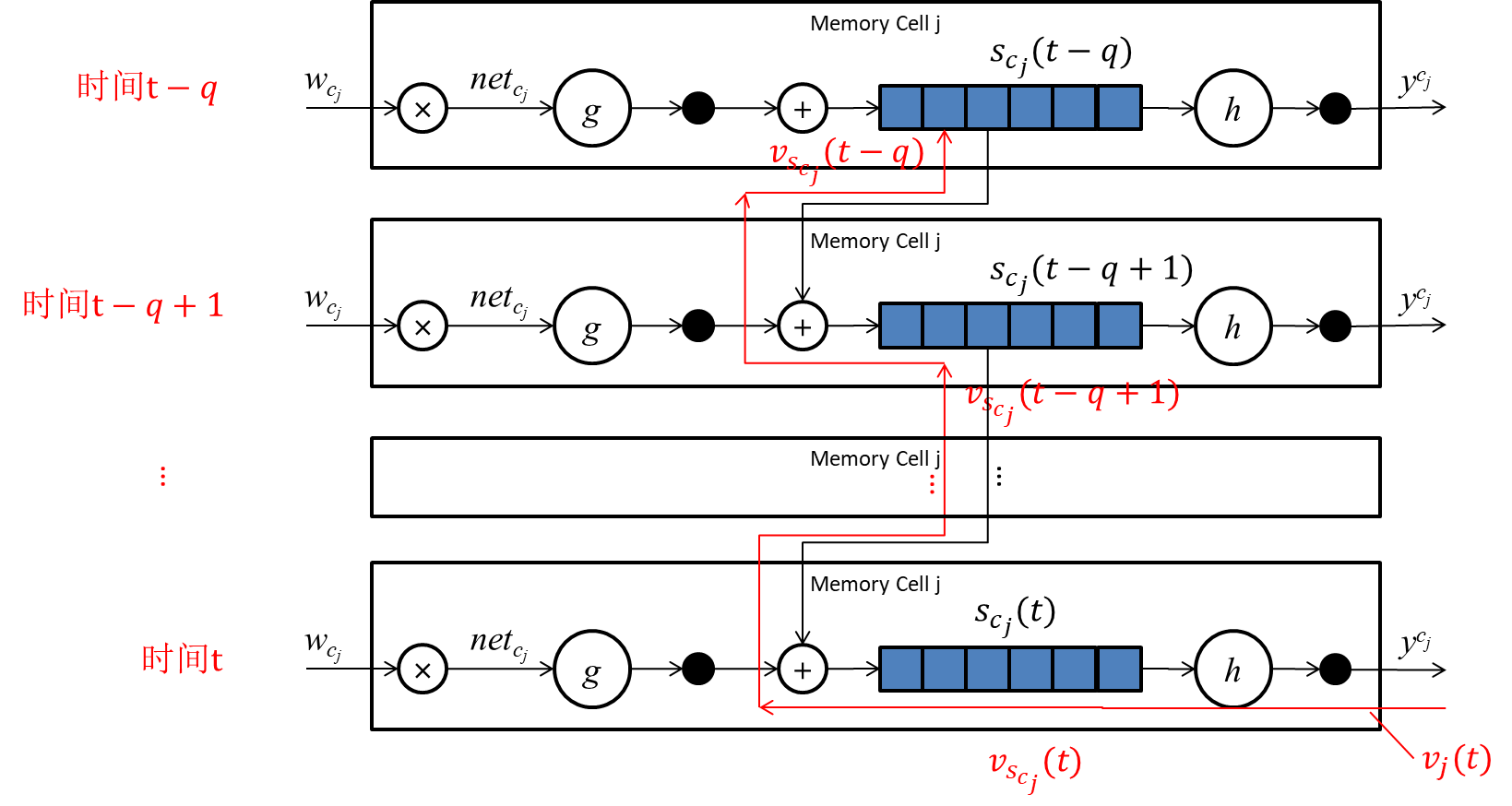
为了便于理解,我们把上边这个传播路径按时间顺序展开一下:
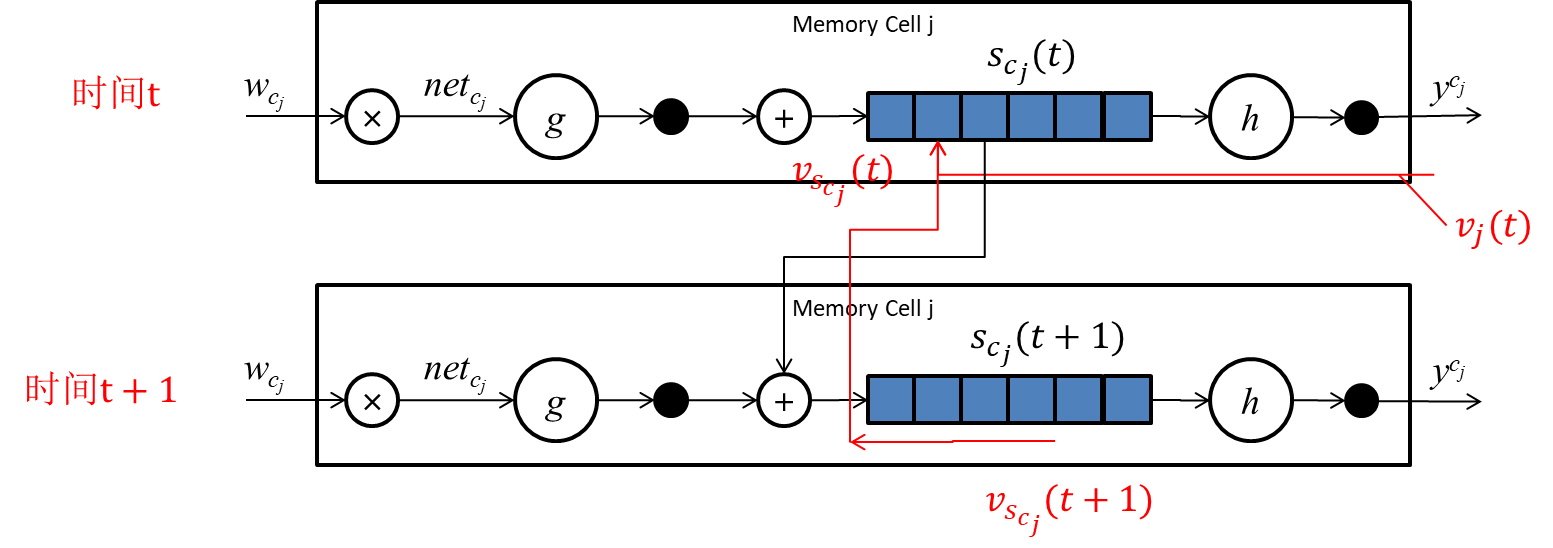
从上图我们可以明显地看出来,因为
s
c
j
(
t
)
s_{c_j}(t)
scj(t)同时作为两个分支的输入,因此
v
s
c
j
(
t
)
v_{s_{c_j}}(t)
vscj(t)等于两个分支传过来的误差值之和:
v
s
c
j
(
t
)
=
∂
s
c
j
(
t
+
1
)
∂
s
c
j
(
t
)
v
s
c
j
(
t
+
1
)
+
∂
y
c
j
(
t
)
∂
s
c
j
(
t
)
v
j
(
t
)
.
(33)
v_{s_{c_j}}(t) = \frac{\partial s_{c_j}(t+1)}{\partial s_{c_j}(t)}v_{s_{c_j}}(t+1) + \frac{\partial y^{c_j}(t)}{\partial s_{c_j}(t)}v_j(t)\tag{33}.
vscj(t)=∂scj(t)∂scj(t+1)vscj(t+1)+∂scj(t)∂ycj(t)vj(t).(33)
6.4 CEC之间的误差流
接下来算一个中间公式,后边有用:
∂
v
j
(
t
)
∂
v
s
c
j
(
t
+
1
)
=
∂
∑
u
w
i
c
j
v
i
(
t
+
1
)
∂
v
s
c
j
(
t
+
1
)
(
代入式
31
∗
)
=
∑
u
w
u
c
j
∂
v
u
(
t
+
1
)
∂
v
s
c
j
(
t
+
1
)
=
0.
(34)
\begin{aligned} \frac{\partial v_j(t)}{\partial v_{s_{c_j}}(t+1)}&= \frac{\partial \sum_u w_{ic_j}v_i(t+1)}{\partial v_{s_{c_j}}(t+1)}&(代入式31*)\\ &=\sum_u w_{uc_j}\frac{\partial v_u(t+1)}{\partial v_{s_{c_j}}(t+1)}\\ &=0\tag{34}. \end{aligned}
∂vscj(t+1)∂vj(t)=∂vscj(t+1)∂∑uwicjvi(t+1)=u∑wucj∂vscj(t+1)∂vu(t+1)=0.(代入式31∗)(34)
为什么
∑
u
w
u
c
j
∂
v
u
(
t
+
1
)
∂
v
s
c
j
(
t
+
1
)
=
0
\sum_u w_{uc_j}\frac{\partial v_u(t+1)}{\partial v_{s_{c_j}}(t+1)}=0
∑uwucj∂vscj(t+1)∂vu(t+1)=0呢?我们用
v
y
u
(
t
)
v_{y^u}(t)
vyu(t)来表示
t
t
t时刻传导到
y
u
y^u
yu处的误差值,我们把LSTM模型按时间展开一下:
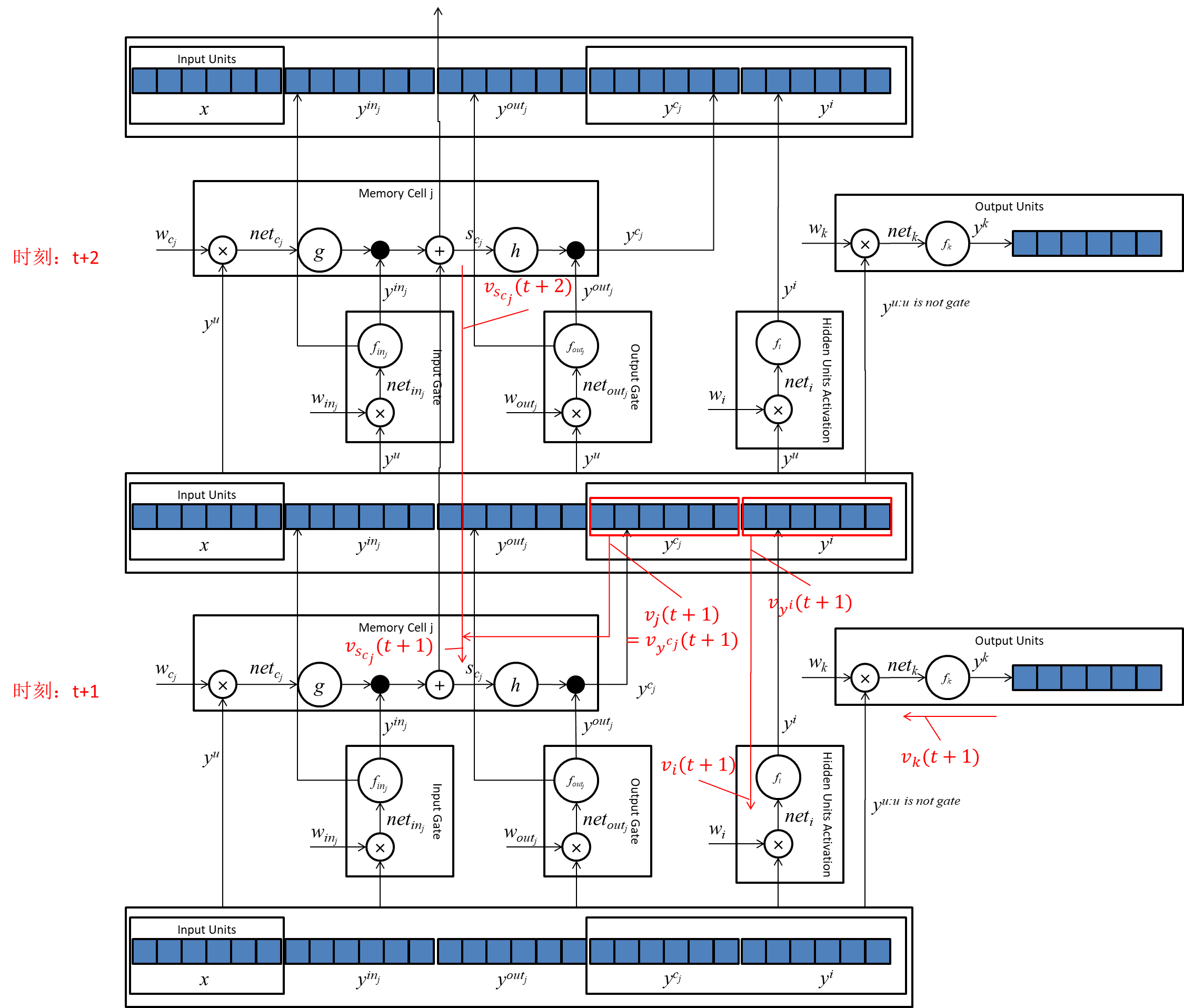
由于:
∑
u
:
u
n
o
g
a
t
e
n
o
m
e
m
o
r
y
c
e
l
l
w
u
c
j
v
u
(
t
+
1
)
=
∑
i
w
i
c
j
v
i
(
t
+
1
)
+
∑
k
w
k
c
j
v
i
(
t
+
1
)
\sum_{u:\ u\ no\ gate\ no\ memory\ cell} w_{uc_j}v_u(t+1)=\sum_{i} w_{ic_j}v_i(t+1) + \sum_{k} w_{kc_j}v_i(t+1)
u: u no gate no memory cell∑wucjvu(t+1)=i∑wicjvi(t+1)+k∑wkcjvi(t+1)
可得:
∑
u
w
u
c
j
∂
v
u
(
t
+
1
)
∂
v
s
c
j
(
t
+
1
)
=
∑
i
w
i
c
j
∂
v
i
(
t
+
1
)
∂
v
s
c
j
(
t
+
1
)
+
∑
k
w
k
c
j
∂
v
k
(
t
+
1
)
∂
v
s
c
j
(
t
+
1
)
\sum_u w_{uc_j}\frac{\partial v_u(t+1)}{\partial v_{s_{c_j}}(t+1)}=\sum_{i}\frac{w_{ic_j}\partial v_i(t+1)}{\partial v_{s_{c_j}}(t+1)} + \sum_{k} \frac{w_{kc_j}\partial v_k(t+1)}{\partial v_{s_{c_j}}(t+1)}
u∑wucj∂vscj(t+1)∂vu(t+1)=i∑∂vscj(t+1)wicj∂vi(t+1)+k∑∂vscj(t+1)wkcj∂vk(t+1)
通过上图,我们容易看出,
v
i
(
t
+
1
)
v_i(t+1)
vi(t+1)与
v
s
c
j
(
t
+
1
)
v_{s_{c_j}}(t+1)
vscj(t+1)互相独立,且
v
k
(
t
+
1
)
v_k(t+1)
vk(t+1)与
v
s
c
j
(
t
+
1
)
v_{s_{c_j}}(t+1)
vscj(t+1)互相独立,因此
w
i
c
j
∂
v
i
(
t
+
1
)
∂
v
s
c
j
(
t
+
1
)
=
0
,
∀
i
\frac{w_{ic_j}\partial v_i(t+1)}{\partial v_{s_{c_j}}(t+1)}=0, \forall i
∂vscj(t+1)wicj∂vi(t+1)=0,∀i,且
w
k
c
j
∂
v
k
(
t
+
1
)
∂
v
s
c
j
(
t
+
1
)
=
0
,
∀
k
\frac{w_{kc_j}\partial v_k(t+1)}{\partial v_{s_{c_j}}(t+1)}=0, \forall k
∂vscj(t+1)wkcj∂vk(t+1)=0,∀k。所以式子34得证。
此时我们来计算时刻
t
+
1
t+1
t+1流入
s
c
j
s_{c_j}
scj的误差值对
t
t
t时刻,流入
s
c
j
s_{c_j}
scj的误差值的影响:
∂
v
s
c
j
(
t
)
∂
v
s
c
j
(
t
+
1
)
=
∂
s
c
j
(
t
+
1
)
∂
s
c
j
(
t
)
∂
v
s
c
j
(
t
+
1
)
∂
v
s
c
j
(
t
+
1
)
+
∂
y
c
j
(
t
)
∂
s
c
j
(
t
)
∂
v
j
(
t
)
∂
v
s
c
j
(
t
+
1
)
(代入式
33
)
=
∂
s
c
j
(
t
+
1
)
∂
s
c
j
(
t
)
(代入式
34
)
≈
t
r
1
(代入式
30
)
.
(35)
\begin{aligned} \frac{\partial v_{s_{c_j}}(t)}{\partial v_{s_{c_j}}(t+1)} &= \frac{\frac{\partial s_{c_j}(t+1)}{\partial s_{c_j}(t)}\partial v_{s_{c_j}}(t+1)}{\partial v_{s_{c_j}}(t+1)} + \frac{\frac{\partial y^{c_j}(t)}{\partial s_{c_j}(t)}\partial v_j(t)}{\partial v_{s_{c_j}}(t+1)}&(代入式33)\\ &=\frac{\partial s_{c_j}(t+1)}{\partial s_{c_j}(t)}& (代入式34)\\ &\approx_{tr}1&(代入式30)\tag{35}. \end{aligned}
∂vscj(t+1)∂vscj(t)=∂vscj(t+1)∂scj(t)∂scj(t+1)∂vscj(t+1)+∂vscj(t+1)∂scj(t)∂ycj(t)∂vj(t)=∂scj(t)∂scj(t+1)≈tr1(代入式33)(代入式34)(代入式30).(35)
式35意味着:
v
s
c
j
(
t
)
=
v
s
c
j
(
t
+
1
)
+
C
.
v_{s_{c_j}}(t) = v_{s_{c_j}}(t+1) + C.
vscj(t)=vscj(t+1)+C.
记忆单元内部的误差值是恒定的,或者说,
t
+
1
t+1
t+1时刻,流到
v
s
c
j
v_{s_{c_j}}
vscj的误差值是多少,再往上流到
t
t
t时刻的
v
s
c
j
v_{s_{c_j}}
vscj那里,就还是多少。(这是最理想的情况,我们这个模型还有一个
C
C
C)。
6.5 记忆单元的误差值计算
记忆单元输入处的误差值
v
c
j
(
t
)
v_{c_j}(t)
vcj(t)为:
v
c
j
(
t
)
=
∂
g
(
n
e
t
c
j
(
t
)
)
∂
n
e
t
c
j
(
t
)
∂
s
c
j
(
t
)
∂
g
(
n
e
t
c
j
(
t
)
)
v
s
c
j
(
t
)
.
(36)
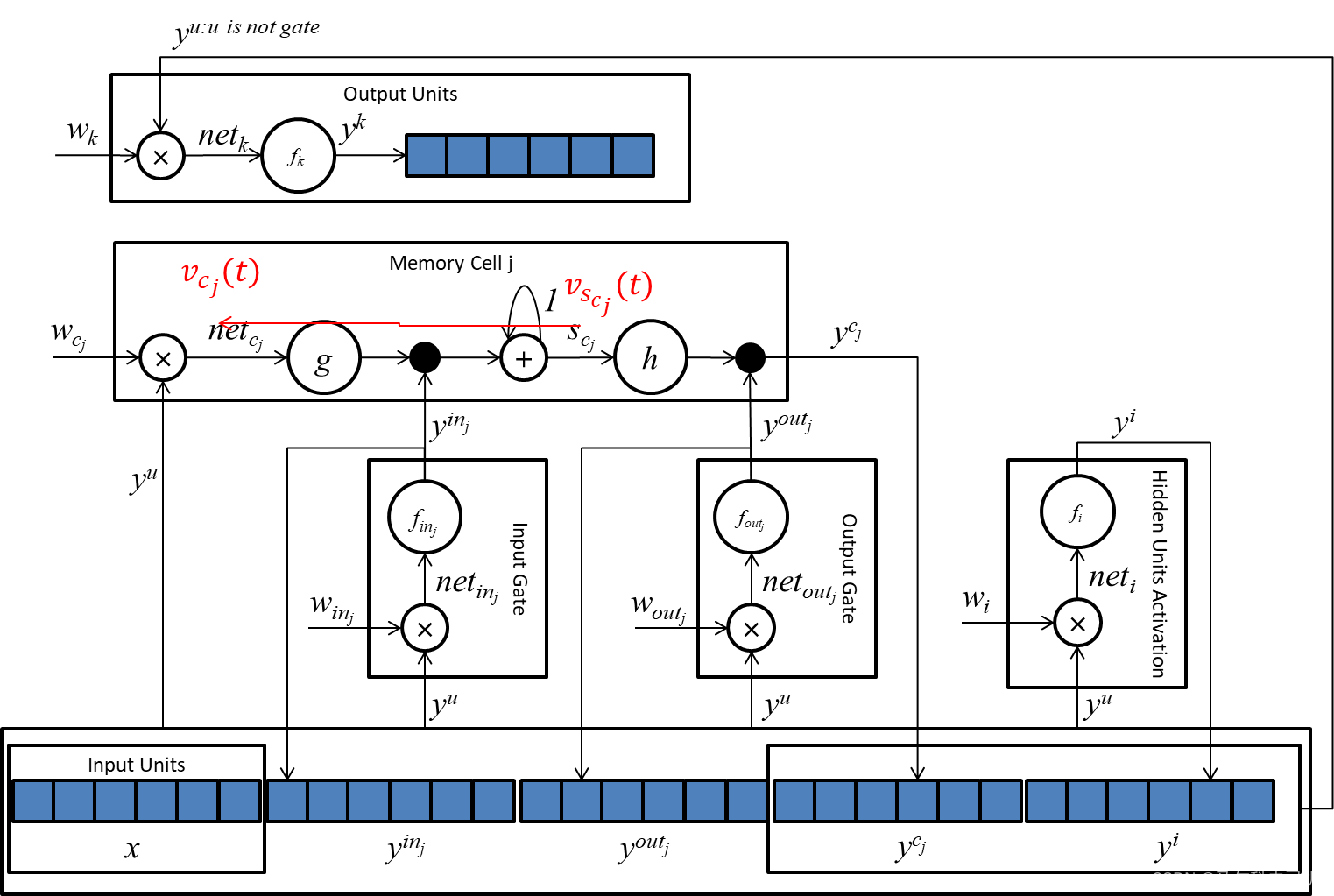
v_{c_j}(t)=\frac{\partial g(net_{c_j}(t))}{\partial net_{c_j}(t)}\frac{\partial s_{c_j}(t)}{\partial g(net_{c_j}(t))}v_{s_{c_j}}(t)\tag{36}.
vcj(t)=∂netcj(t)∂g(netcj(t))∂g(netcj(t))∂scj(t)vscj(t).(36)
这个公式太简单了,不需要再进一步解释。我们放个误差流的示意图用以说明上式所说的标记的位置:
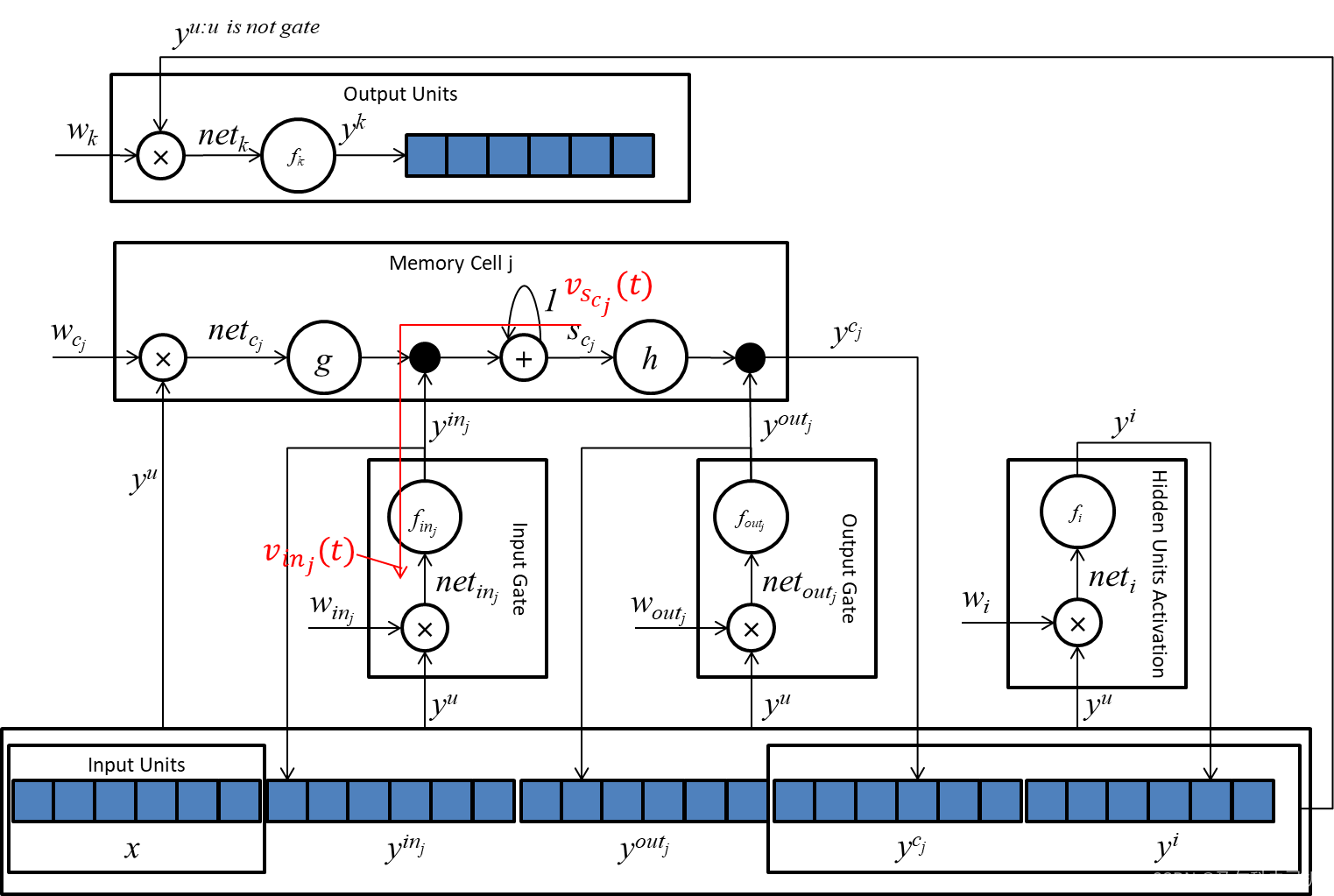
6.6 输入门的误差值计算
v
i
n
j
(
t
)
≈
t
r
∂
y
i
n
j
(
t
)
∂
n
e
t
i
n
j
(
t
)
∂
s
c
j
(
t
)
∂
y
i
n
j
(
t
)
v
s
c
j
(
t
)
.
(37)
v_{in_j}(t)\approx_{tr}\frac{\partial y^{in_j}(t)}{\partial net_{in_j}(t)}\frac{\partial s_{c_j}(t)}{\partial y_{in_j}(t)}v_{s_{c_j}}(t)\tag{37}.
vinj(t)≈tr∂netinj(t)∂yinj(t)∂yinj(t)∂scj(t)vscj(t).(37)
误差值传播示意图:
6.7 外部误差流的计算
在
t
+
1
t+1
t+1时刻,各个门或记忆单元(记为
l
l
l)的误差值
v
l
(
t
+
1
)
v_l(t+1)
vl(t+1),沿着
w
l
v
w_{lv}
wlv传播到上一个时间时刻
t
t
t的某一个记忆单元、门、输出单元或者隐藏单元(记为
v
v
v)中去,这就叫外部误差流(external error flow),我们计算一下任何节点
v
v
v在
t
t
t时刻收到的外部误差值(记为
v
v
e
(
t
)
v_v^e(t)
vve(t)):
v
v
e
(
t
)
=
∂
y
v
(
t
)
∂
n
e
t
v
(
t
)
∑
l
∂
n
e
t
l
(
t
+
1
)
∂
y
v
(
t
)
v
l
(
t
+
1
)
=
∂
y
v
(
t
)
∂
n
e
t
v
(
t
)
(
∂
n
e
t
o
u
t
j
(
t
+
1
)
∂
y
v
(
t
)
v
o
u
t
j
(
t
+
1
)
+
∂
n
e
t
i
n
j
(
t
+
1
)
∂
y
v
(
t
)
v
i
n
j
(
t
+
1
)
+
∂
n
e
t
c
j
(
t
+
1
)
∂
y
v
(
t
)
(38)
\begin{aligned} v_v^e(t) &= \frac{\partial y^v(t)}{\partial net_v(t)}\sum_l \frac{\partial net_l(t+1)}{\partial y^v(t)}v_l(t+1)\tag{38}\\ &= \frac{\partial y^v(t)}{\partial net_v(t)}( \frac{\partial net_{out_j}(t+1)}{\partial y^v(t)}v_{out_j}(t+1)+ \frac{\partial net_{in_j}(t+1)}{\partial y^v(t)}v_{in_j}(t+1) + \frac{\partial net_{c_j}(t+1)}{\partial y^v(t)} \end{aligned}
vve(t)=∂netv(t)∂yv(t)l∑∂yv(t)∂netl(t+1)vl(t+1)=∂netv(t)∂yv(t)(∂yv(t)∂netoutj(t+1)voutj(t+1)+∂yv(t)∂netinj(t+1)vinj(t+1)+∂yv(t)∂netcj(t+1)(38)
可以通过下图理解外部误差的传播路径:
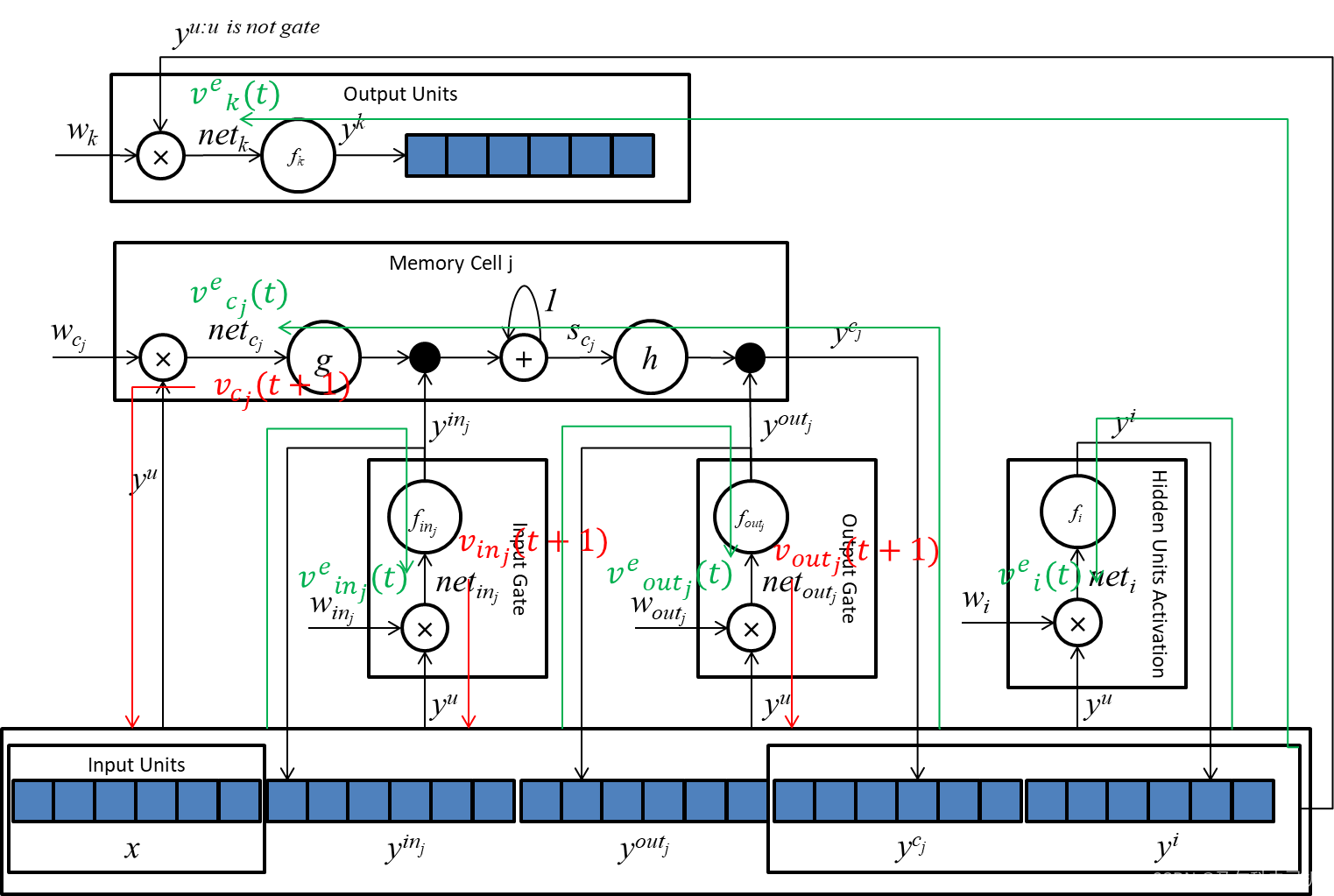
此时我们可以得到外部误差与记忆单元
v
v
e
(
t
−
1
)
v_v^e(t-1)
vve(t−1)与
v
j
(
t
)
v_j(t)
vj(t)的关系,先看下边的传播路径示意图理解一下这个公式想计算的是什么东西,我们这里为了便于理解,只画出
v
=
i
n
j
v=in_j
v=inj的情况:

∂
v
v
e
(
t
−
1
)
∂
v
j
(
t
)
=
∂
y
v
(
t
−
1
)
∂
n
e
t
v
(
t
−
1
)
(
∂
v
o
u
t
j
(
t
)
∂
v
j
(
t
)
∂
n
e
t
o
u
t
j
(
t
)
∂
y
v
(
t
−
1
)
+
∂
v
i
n
j
(
t
)
∂
v
j
(
t
)
∂
n
e
t
i
n
j
(
t
)
∂
y
v
(
t
−
1
)
+
∂
v
c
j
(
t
)
∂
v
j
(
t
)
∂
n
e
t
c
j
(
t
)
∂
y
v
(
t
−
1
)
)
≈
t
r
0.
(39)
\begin{aligned} \frac{\partial v_v^e(t-1)}{\partial v_j(t)}&= \frac{\partial y^v(t-1)}{\partial net_v(t-1)}( \frac{\partial v_{out_j}(t)}{\partial v_j(t)}\frac{\partial net_{out_j}(t)}{\partial y^v(t-1)}+ \frac{\partial v_{in_j}(t)}{\partial v_j(t)}\frac{\partial net_{in_j}(t)}{\partial y^v(t-1)} + \frac{\partial v_{c_j}(t)}{\partial v_j(t)}\frac{\partial net_{c_j}(t)}{\partial y^v(t-1)}) \\ &\approx_{tr}0\tag{39}. \end{aligned}
∂vj(t)∂vve(t−1)=∂netv(t−1)∂yv(t−1)(∂vj(t)∂voutj(t)∂yv(t−1)∂netoutj(t)+∂vj(t)∂vinj(t)∂yv(t−1)∂netinj(t)+∂vj(t)∂vcj(t)∂yv(t−1)∂netcj(t))≈tr0.(39)
根据截断求导规则,上式中的
∂
n
e
t
o
u
t
j
(
t
)
∂
y
v
(
t
−
1
)
≈
t
r
0
\frac{\partial net_{out_j}(t)}{\partial y^v(t-1)}\approx_{tr}0
∂yv(t−1)∂netoutj(t)≈tr0,
∂
n
e
t
i
n
j
(
t
)
∂
y
v
(
t
−
1
)
≈
t
r
0
\frac{\partial net_{in_j}(t)}{\partial y^v(t-1)}\approx_{tr}0
∂yv(t−1)∂netinj(t)≈tr0,
∂
n
e
t
c
j
(
t
)
∂
y
v
(
t
−
1
)
≈
t
r
0
\frac{\partial net_{c_j}(t)}{\partial y^v(t-1)}\approx_{tr}0
∂yv(t−1)∂netcj(t)≈tr0,因此上式应用截断求导之后为0。
上式的意义就在于,证明了应用截断规则后,从记忆单元出口处的误差值,不会经由 i n j , o u t j , c j in_j,out_j,c_j inj,outj,cj传播到其他任何门和单元。(其实用眼睛看也可以一眼看出来)
6.8 记忆单元内部的误差流计算
最后,让我们来关注从记忆单元出口处的误差,传递到记忆单元内的CEC的情况。这也是整个模型中唯一的错误信息会跨时间步传递的误差流。
给定时间步
q
q
q,我们计算
∂
v
s
c
j
(
t
−
q
)
∂
v
j
(
t
)
\frac{\partial v_{s_{c_j}}(t-q)}{\partial v_j(t)}
∂vj(t)∂vscj(t−q):
当
q
=
0
q=0
q=0时,我们可以看下图的误差传播路径:
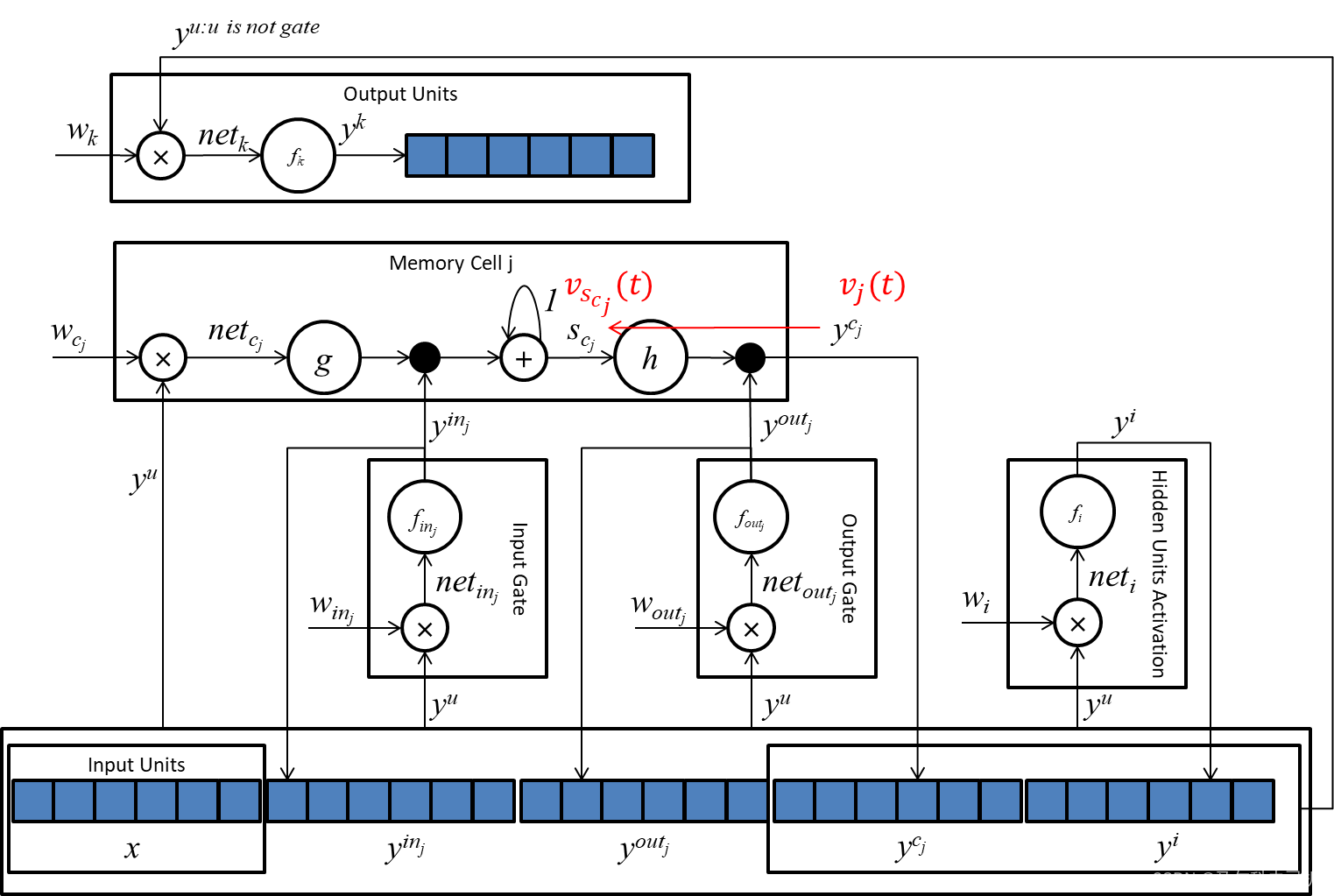
根据上图,容易得到:
∂
v
s
c
j
(
t
−
q
)
∂
v
j
(
t
)
=
∂
v
s
c
j
(
t
)
∂
v
j
(
t
)
=
∂
y
c
j
(
t
)
∂
s
c
j
(
t
)
\begin{aligned} \frac{\partial v_{s_{c_j}}(t-q)}{\partial v_j(t)}&=\frac{\partial v_{s_{c_j}}(t)}{\partial v_j(t)}=\frac{\partial y^{c_j}(t)}{\partial s_{c_j}(t)} \end{aligned}
∂vj(t)∂vscj(t−q)=∂vj(t)∂vscj(t)=∂scj(t)∂ycj(t)
当
q
=
1
q=1
q=1时,误差传播路径如下图所示(隐藏了无关的单元,只保留记忆单元):
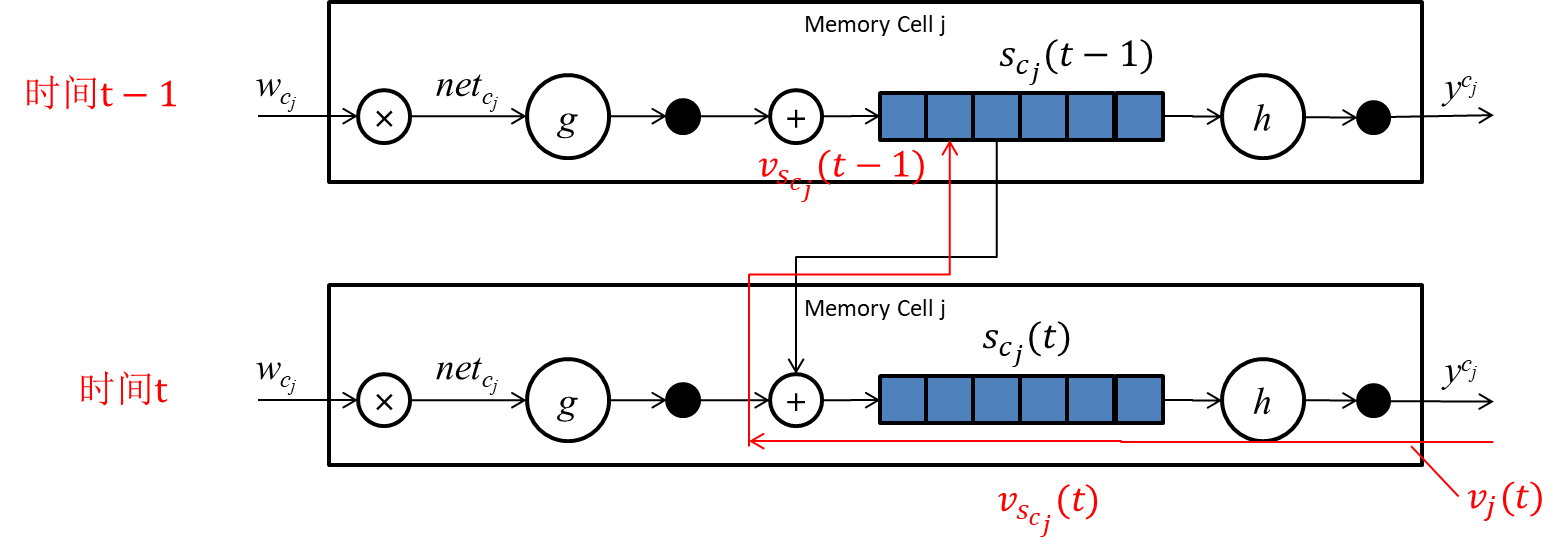
∂
v
s
c
j
(
t
−
q
)
∂
v
j
(
t
)
=
∂
v
s
c
j
(
t
−
1
)
∂
v
j
(
t
)
≈
t
r
∂
v
j
(
t
)
∂
y
c
j
(
t
)
∂
s
c
j
(
t
)
∂
s
c
j
(
t
)
∂
s
c
j
(
t
−
1
)
∂
v
j
(
t
)
≈
t
r
∂
y
c
j
(
t
)
∂
s
c
j
(
t
)
∂
s
c
j
(
t
)
∂
s
c
j
(
t
−
1
)
≈
t
r
∂
s
c
j
(
t
)
∂
s
c
j
(
t
−
1
)
∂
v
s
c
j
(
t
)
∂
v
j
(
t
)
\begin{aligned} \frac{\partial v_{s_{c_j}}(t-q)}{\partial v_j(t)}&=\frac{\partial v_{s_{c_j}}(t-1)}{\partial v_j(t)}\\ &\approx_{tr}\frac{\partial v_j(t)\frac{\partial y^{c_j}(t)}{\partial s_{c_j}(t)}\frac{\partial s_{c_j}(t)}{\partial s_{c_j}(t-1)}}{\partial v_j(t)}\\ &\approx_{tr}\frac{\partial y^{c_j}(t)}{\partial s_{c_j}(t)}\frac{\partial s_{c_j}(t)}{\partial s_{c_j}(t-1)}\\ &\approx_{tr}\frac{\partial s_{c_j}(t)}{\partial s_{c_j}(t-1)}\frac{\partial v_{s_{c_j}}(t)}{\partial v_j(t)} \end{aligned}
∂vj(t)∂vscj(t−q)=∂vj(t)∂vscj(t−1)≈tr∂vj(t)∂vj(t)∂scj(t)∂ycj(t)∂scj(t−1)∂scj(t)≈tr∂scj(t)∂ycj(t)∂scj(t−1)∂scj(t)≈tr∂scj(t−1)∂scj(t)∂vj(t)∂vscj(t)
当
q
>
1
q>1
q>1时:
∂ v s c j ( t − q ) ∂ v j ( t ) ≈ t r ∂ v j ( t ) ∂ y c j ( t ) ∂ s c j ( t − q + 1 ) ∂ s c j ( t − q + 1 ) ∂ s c j ( t − q ) ∂ v j ( t ) ≈ t r ∂ y c j ( t ) ∂ s c j ( t − q + 1 ) ∂ s c j ( t − q + 1 ) ∂ s c j ( t − q ) ≈ t r ∂ v s c j ( t − q + 1 ) ∂ v j ( t ) ∂ s c j ( t − q + 1 ) ∂ s c j ( t − q ) \begin{aligned} \frac{\partial v_{s_{c_j}}(t-q)}{\partial v_j(t)}&\approx_{tr}\frac{\partial v_j(t)\frac{\partial y^{c_j}(t)}{\partial s_{c_j}(t-q+1)}\frac{\partial s_{c_j}(t-q+1)}{\partial s_{c_j}(t-q)}}{\partial v_j(t)}\\ &\approx_{tr}\frac{\partial y^{c_j}(t)}{\partial s_{c_j}(t-q+1)}\frac{\partial s_{c_j}(t-q+1)}{\partial s_{c_j}(t-q)}\\ &\approx_{tr}\frac{\partial v_{s_{c_j}}(t-q+1)}{\partial v_j(t)}\frac{\partial s_{c_j}(t-q+1)}{\partial s_{c_j}(t-q)} \end{aligned} ∂vj(t)∂vscj(t−q)≈tr∂vj(t)∂vj(t)∂scj(t−q+1)∂ycj(t)∂scj(t−q)∂scj(t−q+1)≈tr∂scj(t−q+1)∂ycj(t)∂scj(t−q)∂scj(t−q+1)≈tr∂vj(t)∂vscj(t−q+1)∂scj(t−q)∂scj(t−q+1)
因此我们可得:
∂
v
s
c
j
(
t
−
q
)
∂
v
j
(
t
)
≈
t
r
{
∂
y
c
j
(
t
)
∂
s
c
j
(
t
)
(
q
=
0
)
∂
s
c
j
(
t
−
q
+
1
)
∂
s
c
j
(
t
−
q
)
∂
v
s
c
j
(
t
−
q
+
1
)
∂
v
j
(
t
)
(
q
>
0
)
.
(40)
\frac{\partial v_{s_{c_j}}(t-q)}{\partial v_j(t)}\approx_{tr} \begin{cases} \frac{\partial y^{c_j}(t)}{\partial s_{c_j}(t)} &(q=0)\\ \frac{\partial s_{c_j}(t-q+1)}{\partial s_{c_j}(t-q)}\frac{\partial v_{s_{c_j}}(t-q+1)}{\partial v_j(t)}&(q>0) \end{cases}\tag{40}.
∂vj(t)∂vscj(t−q)≈tr⎩
⎨
⎧∂scj(t)∂ycj(t)∂scj(t−q)∂scj(t−q+1)∂vj(t)∂vscj(t−q+1)(q=0)(q>0).(40)
将式40扩展为计算记忆节点在时刻
t
t
t的误差值,传播到
t
−
q
t-q
t−q时刻任意节点
v
v
v时的误差,误差传播路经如下图所示:
从上图可知在
t
−
q
t-q
t−q时刻,只有
n
e
t
i
n
j
net_{in_j}
netinj,
n
e
t
c
j
net_{c_j}
netcj处,即
v
∈
{
i
n
j
,
c
j
}
v\in\{in_j,c_j\}
v∈{inj,cj}时,可以得到
v
j
(
t
)
v_j(t)
vj(t)传过来的非零误差。其他位置都是0。我们标记任意节点
v
v
v在
t
−
q
t-q
t−q时刻收到的误差信息为
v
v
(
t
−
q
)
v_v(t-q)
vv(t−q),我们计算
t
t
t时刻记忆单元出口处与
v
v
(
t
−
q
)
v_v(t-q)
vv(t−q)之间的误差流:
∂
v
v
(
t
−
q
)
∂
v
j
(
t
)
≈
t
r
∂
v
v
(
t
−
q
)
∂
v
s
c
j
(
t
−
q
)
∂
v
s
c
j
(
t
−
q
)
∂
v
j
(
t
)
≈
t
r
∂
v
v
(
t
−
q
)
∂
v
s
c
j
(
t
−
q
)
∂
s
c
j
(
t
−
q
+
1
)
∂
s
c
j
(
t
−
q
)
∂
v
s
c
j
(
t
−
q
+
1
)
∂
v
j
(
t
)
≈
t
r
∂
v
v
(
t
−
q
)
∂
v
s
c
j
(
t
−
q
)
(
∂
s
c
j
(
t
−
q
+
1
)
∂
s
c
j
(
t
−
q
)
∂
s
c
j
(
t
−
q
+
2
)
∂
s
c
j
(
t
−
q
+
1
)
∂
s
c
j
(
t
−
q
+
3
)
∂
s
c
j
(
t
−
q
+
2
)
⋯
∂
s
c
j
(
t
+
1
)
∂
s
c
j
(
t
)
)
∂
v
s
c
j
(
t
)
∂
v
j
(
t
)
≈
t
r
∂
v
v
(
t
−
q
)
∂
v
s
c
j
(
t
−
q
)
(
∏
m
=
0
q
∂
s
c
j
(
t
−
m
+
1
)
∂
s
c
j
(
t
−
m
)
)
∂
v
s
c
j
(
t
)
∂
v
j
(
t
)
≈
t
r
∂
v
v
(
t
−
q
)
∂
v
s
c
j
(
t
−
q
)
∂
v
s
c
j
(
t
)
∂
v
j
(
t
)
≈
t
r
y
o
u
t
j
(
t
)
h
′
(
s
c
j
(
t
)
)
{
g
′
(
n
e
t
c
j
(
t
−
q
)
)
y
i
n
j
(
t
−
q
)
v
=
c
j
g
(
n
e
t
c
j
(
t
−
q
)
)
f
i
n
j
′
(
n
e
t
i
n
j
(
t
−
q
)
)
v
=
i
n
j
0
O
t
h
e
r
w
i
s
e
.
(41)
\begin{aligned} \frac{\partial v_v(t-q)}{\partial v_j(t)}&\approx_{tr}\frac{\partial v_v(t-q)}{\partial v_{s_{c_j}}(t-q)}\frac{\partial v_{s_{c_j}}(t-q)}{\partial v_j(t)}\\ &\approx_{tr} \frac{\partial v_v(t-q)}{\partial v_{s_{c_j}}(t-q)}\frac{\partial s_{c_j}(t-q+1)}{\partial s_{c_j}(t-q)}\frac{\partial v_{s_{c_j}}(t-q+1)}{\partial v_j(t)}\\ &\approx_{tr} \frac{\partial v_v(t-q)}{\partial v_{s_{c_j}}(t-q)}(\frac{\partial s_{c_j}(t-q+1)}{\partial s_{c_j}(t-q)}\frac{\partial s_{c_j}(t-q+2)}{\partial s_{c_j}(t-q+1)}\frac{\partial s_{c_j}(t-q+3)}{\partial s_{c_j}(t-q+2)}\cdots\frac{\partial s_{c_j}(t+1)}{\partial s_{c_j}(t)})\frac{\partial v_{s_{c_j}}(t)}{\partial v_j(t)}\\ &\approx_{tr}\frac{\partial v_v(t-q)}{\partial v_{s_{c_j}}(t-q)}(\prod_{m=0}^q\frac{\partial s_{c_j}(t-m+1)}{\partial s_{c_j}(t-m)})\frac{\partial v_{s_{c_j}}(t)}{\partial v_j(t)}\\ &\approx_{tr}\frac{\partial v_v(t-q)}{\partial v_{s_{c_j}}(t-q)}\frac{\partial v_{s_{c_j}}(t)}{\partial v_j(t)}\\ &\approx_{tr}y^{out_j}(t)h'(s_{c_j}(t)) \begin{cases} g'(net_{c_j}(t-q))y^{in_j}(t-q)&v=c_j\\ g(net_{c_j}(t-q))f'_{in_j}(net_{in_j}(t-q)) &v=in_j\\ 0&Otherwise \end{cases}\tag{41}. \end{aligned}
∂vj(t)∂vv(t−q)≈tr∂vscj(t−q)∂vv(t−q)∂vj(t)∂vscj(t−q)≈tr∂vscj(t−q)∂vv(t−q)∂scj(t−q)∂scj(t−q+1)∂vj(t)∂vscj(t−q+1)≈tr∂vscj(t−q)∂vv(t−q)(∂scj(t−q)∂scj(t−q+1)∂scj(t−q+1)∂scj(t−q+2)∂scj(t−q+2)∂scj(t−q+3)⋯∂scj(t)∂scj(t+1))∂vj(t)∂vscj(t)≈tr∂vscj(t−q)∂vv(t−q)(m=0∏q∂scj(t−m)∂scj(t−m+1))∂vj(t)∂vscj(t)≈tr∂vscj(t−q)∂vv(t−q)∂vj(t)∂vscj(t)≈tryoutj(t)h′(scj(t))⎩
⎨
⎧g′(netcj(t−q))yinj(t−q)g(netcj(t−q))finj′(netinj(t−q))0v=cjv=injOtherwise.(41)
通过上式可以看出,误差流的变化只有分别与 t t t和 t − q t-q t−q时刻有关,在不同时间步之间流经CEC时未受影响。最后Sepp Hochreiter指出以下几点:
- y o u t j ( t ) y^{out_j}(t) youtj(t)可以在误差流进入记忆单元之前就缩小误差值。也会在之后的训练步骤中降低记忆单元产生的误差值。
- 根据式35可知, v s c j ( t ) = v s c j ( t + 1 ) + C v_{s_{c_j}}(t) = v_{s_{c_j}}(t+1) + C vscj(t)=vscj(t+1)+C,因此随着时间步数的增加, s c j s_{c_j} scj会出现漂移的情况,如果 s c j ( t ) s_{c_j}(t) scj(t)产生一个大值(大正值或大负值),该值会被 h ′ ( s c j ( t ) ) h'(s_{c_j}(t)) h′(scj(t))截断。同时,也可通过给 i n j in_j inj设置适当的偏移量来优化该问题(现在我们通过增加遗忘门解决该问题,这个遗忘门也成为新的标准LSTM模型的一部分)。
- 如果我们给 i n j in_j inj设置了用与抗衡 s c j s_{c_j} scj漂移的反向偏移值,那么会导致 y i n j ( t − q ) y^{in_j}(t-q) yinj(t−q)和 ( n e t i n j ( t − q ) ) (net_{in_j}(t-q)) (netinj(t−q))的值变小,这样的影响对比放任 s c j s_{c_j} scj漂移的影响来说微不足道。
总之一句话,LSTM模型比没有记忆单元的RNN模型好很多。





















 792
792











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








