基于LMS算法的Mackey Glass时间序列预测附Matlab代码

✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，matlab项目合作可私信。

🍎个人主页：Matlab科研工作室

🍊个人信条：格物致知。

⛄ 内容介绍

在自然科学和社会科学各领域中,大量决策问题离不开预测,预测是决策的基础.时间序列是利用现有的历史数据构造模型,进而预测未来.因此,该文首先介绍了定量化的时间序列预测目前采用的一种方法与预测模型,然后在分析时间序列预测相关概念的基础上,研究了其实现方法.

⛄ 部分代码

%% Mackey Glass Time Series Prediction Using Least Mean Square (LMS)

% Author: SHUJAAT KHAN

clc

clear all

close all

%% Loading Time series data

% I generated a series y(t) for t = 0,1, . . . ,3000, using

% mackey glass series equation with the following configurations:

% b = 0.1, a = 0.2, Tau = 20, and the initial conditions y(t - Tau) = 0.

load Dataset\Data.mat 

time_steps=2;

teacher_forcing=1; % recurrent ARMA modelling with forced desired input after defined time steps 

%% Training and Testing datasets

% For training

Tr=Data(100:2500,1);    % Selecting a Interval of series data t = 100~2500

Yr(Tr)=Data(Tr,2);      % Selecting a chuck of series data y(t)

% For testing

Ts=Data(2500:3000,1);   % Selecting a Interval of series data t = 2500~3000

Ys(Ts)=Data(Ts,2);      % Selecting a chuck of series data y(t)

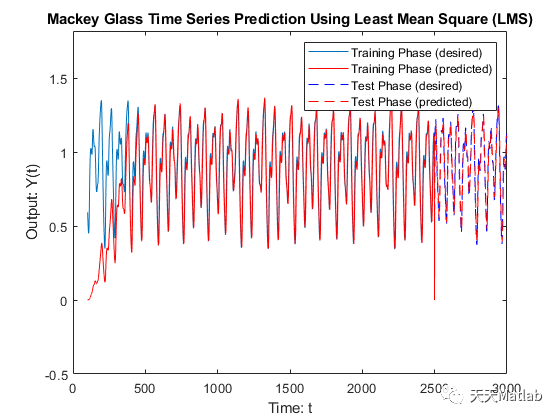
figure(2)

plot(Tr(2*M:end),Yr(Tr(2*M:end)));      % Actual values of mackey glass series

hold on

plot(Tr(2*M:end),Yp(Tr(2*M:end))','r')   % Predicted values during training

plot(Ts,Ys(Ts),'--b');        % Actual unseen data

plot(Ts(1:end-time_steps+1),Yp(Ts(1:end-time_steps+1))','--r');  % Predicted values of mackey glass series (testing)

xlabel('Time: t');

ylabel('Output: Y(t)');

title('Mackey Glass Time Series Prediction Using Least Mean Square (LMS)')

ylim([min(Ys)-0.5, max(Ys)+0.5])

legend('Training Phase (desired)','Training Phase (predicted)','Test Phase (desired)','Test Phase (predicted)');

mitr=10*log10(mean(E(Tr)));  % Minimum MSE of training

mits=10*log10(mean(E(Ts(1:end-time_steps+1))));  % Minimum MSE of testing

display(sprintf('Total training time is %.5f, \nTotal testing time is %.5f \nMSE value during training %.3f (dB),\nMSE value during testing %.3f (dB)', ...

training_time,testing_time,mitr,mits));

⛄ 运行结果

⛄ 参考文献

[1]马飞燕, 李向新. 基于改进麻雀搜索算法-核极限学习机耦合算法的滑坡位移预测模型[J]. 科学技术与工程, 2022(022-005).

⛄ 完整代码

❤️部分理论引用网络文献，若有侵权联系博主删除

❤️ 关注我领取海量matlab电子书和数学建模资料