共軛分布与贝叶斯估计

从最大似然估计（MLE）、最大后验估计（MAP）和贝叶斯估计中的贝叶斯估计我们知道，贝叶斯学派认为给定一组观测数据
$$X=（x_1,x_2,,,,,x_n）$$，估计分布的未知参数$\theta$时，$\theta$应该也是服从一个分布的，所以在计算时，要计算后验概率$P(\theta |X)$的整个分布，而不是像最大后验估计一样，只计算最大值就可以了。但是计算后验概率的整个分布计算量是非常大的，所以就提出来共軛分布的概念，用来简化计算量。

共軛分布的定义

先来看看贝叶斯公式：
$$P(\theta |X)=\frac{P(X|\theta )P(\theta )}{P(X)}$$
其中，$P(X|\theta )$称为似然概率，$P(\theta )$称为先验概率，$P(\theta |X)$称为后验概率。

共轭分布(conjugacy)： 后验概率分布与先验概率分布具有相似的形式，也就是$P(\theta |X)$与$P(\theta )$属于相同类别的分布。那么称$P(\theta |X)和P(\theta )$为共轭分布，同时也称$P(\theta )为似然函数P(X|\theta )$的共轭先验。

共軛分布也就是说，我们的先验概率应该与计算的得到的后验概率具有某种程度上的一致性，这也是符合我们的直观感受的，因为先验概率就是$\theta$的，后验概率也是关于$\theta$的，所以先验概率分布应该与后验概率分布具有相似的形式。

还有就是这样可以形成一个链条，即现在的后验分布可以作为下一次计算的先验分布，如果形式相同，就可以形成一个链条。

共軛分布中几个重要的函数

1. Gamma函数
   
   
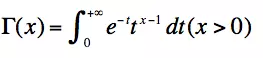
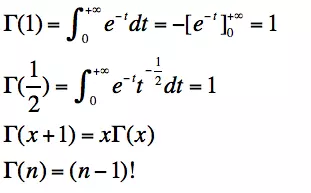
   可以看出, Gamma函数就是将整数域上的阶乘函数推广到了实数域。
2. Beta函数
   

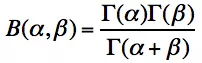
共軛分布中的几个重要的分布

1. Beta分布

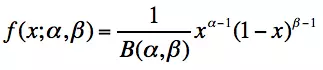
一组定义在区间(0,1)的连续概率分布，有两个参数α和β,且α,β>0
2. Dirichlet分布

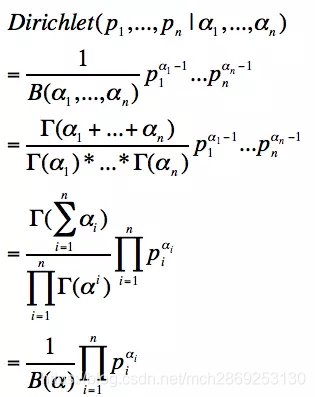
Dirichlet分布也是定义在区间[0, 1]上的多个随机变量的联合概率分布, 上面的公式给出的是n维的狄里克雷分布, 其中$p_i$是变量, 其和为1, ${\alpha }_i$其对应的参数. 最后等式的$\alpha$是一个n维的向量, Dirichlet分布的样本（变量，pi）是多项式分布的参数。
3. 多项式分布

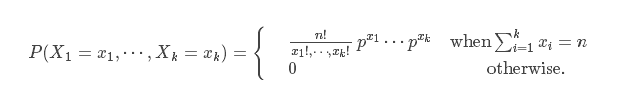
常见的共軛分布

似然函数为高斯分布，先验概率为高斯分布，则后验概率也为高斯分布。
似然函数为二项式分布，先验概率为beta分布，则后验概率也为beta分布。
似然函数为多项式分布，先验概率为Dirichlet分布，则后验概率也为Dirichlet（狄利克雷）分布。

以二项分布与beta分布举例

似然函数正比于二项分布

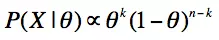
先验概率正比于Beta分布

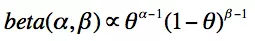
后验概率正比于 (二项分布 x Beta分布)

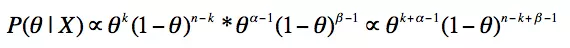
最后我们发现这个贝叶斯估计服从$Beta(a’,b’)$分布的，我们只要用$Beta函数$将它标准化就得到我们的后验概率：

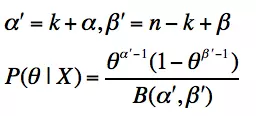
上面其他的两个也可以用这种方法来推导，这里不在赘述。

参考：
共轭先验、共轭分布——为LDA做准备