一、Caffe中的多分类损失函数采用SoftmaxWithLoss层来计算; 损失函数采用的是交叉熵:

其中,k为真是的标签,ak表示每个标签的值,而经过softmax()之后,则返回每一个标签的概率,N表示一个批量的大小,
若去掉批量的概念,即 批量数量为1, 可以理解为只输入一张图片, 来确认它的分类, 则损失函数变为:

那这个交叉熵到底需要怎么理解呢? 他为什么就能作为多分类的损失函数呢? 他在caffe中是怎么实现的呢?
要理解这几个问题, 首先需要了解下面的预备知识:
二、
2.1信息量:
一个信号包含信息的多少, 通常这样的理解或要求:
1)一个非常有可能发生的事情发生了, 信息量较少;
2) 一个不太可能发生的事情发生了, 信息量较大,更有价值;
因此,定义的自信息公式为:
I(x)= - log(P(x))
其中,P(x)为事件x发生的概率, 由公式可知: 当px较大时, Ix较小; 当px较小时, Ix较大。
这个公式能较好的反应Px所携有的信息量。
2.2 熵
熵是信息量的期望, 表示随机变量的确定性的度量, 既然是期望,则很容易写出公式:
H(x)= - Ep*log(px),
对于二分类问题, 即X要么取0,要么取1;
则熵H(x)=-[ P(X=0)*log(P(X=0)) +(1-P(X=1))*log(1-P(X=1)) ]
2.3 交叉熵
表示两个分布 距离的度量。
H(x)= - Ep*log(qx), (3)
其中p和q 分别表示两个分布; 若这两个分布完全相同, p=x的位置, q也非常确定=x(概率qx=1), 则-log(qx)=0,两者的Hx维0;
若两个分布差距很大,即在p=x处, q有很小的概率=x, 即 qx很小, 则-log(qx)会很大, 从而导致两者的交叉熵很大。
因此, 交叉熵是衡量两个分布的工具;
2.4 交叉熵的应用:
回归到机器学习上, 其实也是两个分布的弥合过程, 一个是带有标签的训练数据的分布, 另一个神经网络参数的预测数据分布, 怎么利用交叉熵呢?
比如,我们要预测一张图片上有没有人脸, 我们输入x ----> 通过某种映射f(x)来得到0和1, 1表示有人脸,0表示没有人脸, 但这个映射到底是什么呢???
不过幸运的是,大数据的到来,让我们有了很多这样的图片, 同时我们也知道它有没有人脸, 即 我们有了 x------>y, 即我们有x(像素)和y(标签), 但我们还是不知道映射关系f(x)到底是什么, 但我们可以通过学习来拟合这个映射f(x), 这里有两个分布:一个是带有标签的训练数据的分布,这个分布是真是存才,并且输出概率是确定的, 另一个神经网络参数的预测数据分布,这个是不断学习的。 我们的目标就是通过不断地学习, 让神经网络的模型分布来接近真是的x--》y的分布, 用什么来衡量这两个分布呢,当然是交叉熵了。
但你可能会发现交叉熵的公式3, 与caffe中使用的公式2 不相同, 其实那是因为caffe的softmax分类过程中的结果是唯一确定的, 比如 是(0,0,1,0,0,)表示一个5分类问题, 其中这个图片是属于第三类的, 也就是公式3中的 Ep,表示带标签的分布,他是唯一确定取第三类,即 Ep 只有在第三个维1, 在其余4个都为0,, 因此只剩下了-log(); 表示在真是标签上的大小。
比如, 这个预测的结果也是分类到第三类,且概率为1,即qx=(0,0,1,0,0,), 则 损失函数=-log(1)=0; (正确分类)
如另一个预测结果也是分类到第二类,且概率为1,即qx=(0,1,0,0,0,),则 损失函数=-log(0)很大, (错误分类),当然为了数值稳定, 不可能真的取到0, 而是很接近0;
所以 利用公式2中的交叉熵结果, 如果这个结果较大, 则表示两个分布差别较大(真是分布和预测分布), 表示机器学习的结果不能很好的预测训练集, 跟别说测试集了;当交叉熵的结果(损失函数) 不断减小(梯度下降方法, 随后总结), 趋于很小时, 表示这两个分布近似, 这个模型可以较好预测这个训练分布的数据。 再用来测试训练集。
三、Caffe中的代码实现
template <typename Dtype>
void SoftmaxWithLossLayer<Dtype>::Forward_cpu(
const vector<Blob<Dtype>*>& bottom, const vector<Blob<Dtype>*>& top) {
// The forward pass computes the softmax prob values.
softmax_layer_->Forward(softmax_bottom_vec_, softmax_top_vec_); //调用softmax层来计算分类的概率, 其中softmax_top_vec和prob_data指向同一地址
const Dtype* prob_data = prob_.cpu_data();
const Dtype* label = bottom[1]->cpu_data();
int dim = prob_.count() / outer_num_;
int count = 0;
Dtype loss = 0;
for (int i = 0; i < outer_num_; ++i) {
for (int j = 0; j < inner_num_; j++) {
const int label_value = static_cast<int>(label[i * inner_num_ + j]);
if (has_ignore_label_ && label_value == ignore_label_) {
continue;
}
DCHECK_GE(label_value, 0);
DCHECK_LT(label_value, prob_.shape(softmax_axis_)); //prob_data是从softmax层输出的概率结果,
loss -= log(std::max(prob_data[i * dim + label_value * inner_num_ + j],
Dtype(FLT_MIN))); //仅取出对应label的概率,进行取log操作, 来计算损失函数。
++count;
}
}
top[0]->mutable_cpu_data()[0] = loss / get_normalizer(normalization_, count);
if (top.size() == 2) {
top[1]->ShareData(prob_);
}
}
其实是计算从全连接层进来的分类的概率。
计算步骤如下:
之所以减掉最大值, 是为了数值稳定。 防止取e操作时,出现无穷大, 或 当x很小时, 由于计算机的误差 将分母取为0的错误。
caffe实现如下:
template <typename Dtype>
void SoftmaxLayer<Dtype>::Forward_cpu(const vector<Blob<Dtype>*>& bottom,
const vector<Blob<Dtype>*>& top) {
const Dtype* bottom_data = bottom[0]->cpu_data();
Dtype* top_data = top[0]->mutable_cpu_data();
Dtype* scale_data = scale_.mutable_cpu_data();
int channels = bottom[0]->shape(softmax_axis_);
int dim = bottom[0]->count() / outer_num_;
caffe_copy(bottom[0]->count(), bottom_data, top_data);
// We need to subtract the max to avoid numerical issues, compute the exp,
// and then normalize.
for (int i = 0; i < outer_num_; ++i) {
// initialize scale_data to the first plane
caffe_copy(inner_num_, bottom_data + i * dim, scale_data);
for (int j = 0; j < channels; j++) {
for (int k = 0; k < inner_num_; k++) {
scale_data[k] = std::max(scale_data[k], //取出概率中的大值;
bottom_data[i * dim + j * inner_num_ + k]);
}
}
// subtraction //减掉最大值
caffe_cpu_gemm<Dtype>(CblasNoTrans, CblasNoTrans, channels, inner_num_,
1, -1., sum_multiplier_.cpu_data(), scale_data, 1., top_data);
// exponentiation //取指数
caffe_exp<Dtype>(dim, top_data, top_data);
// sum after exp //求分母的指数和
caffe_cpu_gemv<Dtype>(CblasTrans, channels, inner_num_, 1.,
top_data, sum_multiplier_.cpu_data(), 0., scale_data);
// division //计算除法。
for (int j = 0; j < channels; j++) {
caffe_div(inner_num_, top_data, scale_data, top_data);
top_data += inner_num_;
}
}
}








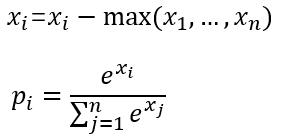














 8638
8638

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








