【数学建模】物资调度的线性约束条件优化模型

1. 问题描述

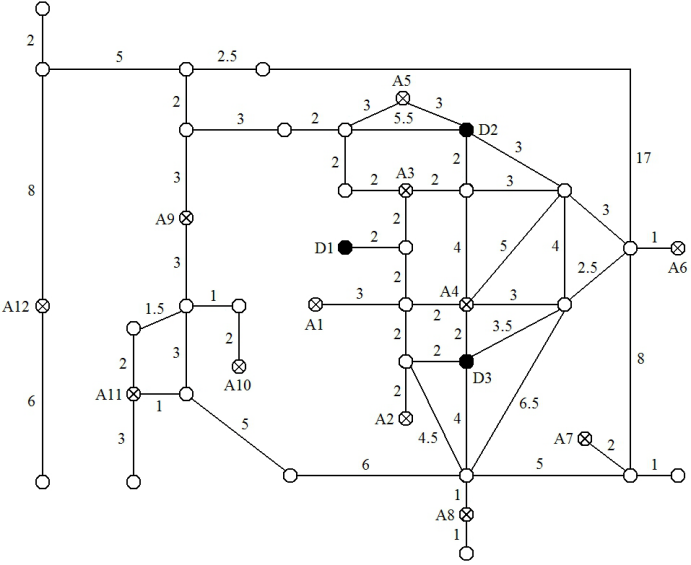
某地区各县市的分布情况如图所示，图中的边表示连接各县市的公路，边权值表示车辆通过该路段所需的时间。

现在 D1, D2, D3 三地突发自然灾害，每天需要应急物资分别为 100 吨、80 吨和 60 吨；而能提供应急物资的县市为 A1, A2, …, A12，它们每天能提供 (30, 15, 15, 20, 35, 40, 30, 20, 10, 25, 25, 30) 吨的应急物资。
如果 A1, A2, …, A12 各地所提供的应急物资，其成本分别为 (2, 4, 5, 3, 1, 6, 2, 3, 6, 1, 5, 5)
万元/ 吨，请设计一份经济快速的应急物资运送方案，使得每天都能保证 D1, D2, D3 三地对应急物资的需求。

2. 基本假设与符号约定

为了简化问题和方便讨论，除问题中给出的假设外，我们进一步做如下的假设和说明：
(1)假设所有物资对于灾区人民的价值是相同的。
在此，我们也约定文中所用符号如下：

运输物资的吨数：

运输吨数	28($A_1$)	34($A_2$)	21($A_3$)	30($A_4$)	17($A_5$)	25($A_6$)	39($A_7$)	40($A_8$)	7($A_9$)	14($A_{10}$)	10($A_{11}$)	3($A_{12}$)
$D_1$	$x_1$	$x_2$	$x_3$	$x_4$	$x_5$	$x_6$	$x_7$	$x_8$	$x_9$	$x_{10}$	$x_{11}$	$x_{12}$
$D_2$	$x_{13}$	$x_{14}$	$x_{15}$	$x_{16}$	$x_{17}$	$x_{18}$	$x_{19}$	$x_{20}$	$x_{21}$	$x_{22}$