（Math）矩阵求导

本文地址：http://blog.csdn.net/mounty_fsc/article/details/51583809

前言

本文为维基百科上矩阵微积分部分的翻译内容。本文为原文的翻译与个人总结，非一一对照翻译。由于水平不足理解不够处，敬请原谅与指出。原文地址https://en.wikipedia.org/wiki/Matrix_calculus。原文为矩阵微积分，本文题为矩阵求导，原因是原文主要介绍的是矩阵微分的内容。

1 简介

矩阵的微积分本质上是多元变量的微积分的问题，只是应用在矩阵空间上而已。

在讨论矩阵微分的时候，有两种布局方式，分子布局，与分母布局，第2,3部分不关注这个问题，第5部分以后介绍两种布局方式。

以下为六种以矩阵形式组织的常见的导数。

类型	标量$y$	向量$\mathbf{y}$	矩阵$\mathbf{Y}$
标量$x$	$\frac{\partial y}{\partial x}$	$\frac{\partial \mathbf{y}}{\partial x}$	$\frac{\partial \mathbf{Y}}{\partial x}$
向量$\mathbf{x}$	$\frac{\partial y}{\partial \mathbf{x}}$	$\frac{\partial \mathbf{y}}{\partial \mathbf{x}}$
矩阵$\mathbf{X}$	$\frac{\partial y}{\partial \mathbf{X}}$

其他三种方式并不常用，且符号也没有统一的认识。

2 符号

1. 矩阵
   $M(n,m)$表示$n$行$m$列的实矩阵，一般使用加粗大写字母表示，如$\mathbf{A,X,Y}$等。

2. 向量
   $M(n,1)$为列向量，一般用小写加粗表示，如$\mathbf{a,x,y}$等。

3. 标量
   $M(1,1)$为标量，一般用小写斜体表示，如$a,x,y$等。

4. 其他
   $X^T$为转置，$tr(X)$为迹，$det(X)$为行列式。字母表前半$(a,b,c,\cdots)$为常量，后半$(t,x,y,\cdots)为变量$

3 关于向量的导数

以分子布局来介绍，仅出于说明目的，不代表分子布局优于分母布局。

3.1 向量关于标量求导

向量$\mathbf{y}=\left[ \begin{array}{c} y_1\\ y_2 \\ \vdots \\ y_m \end{array} \right]$关于标量$x$求导可以表示为$\frac{\partial \mathbf{y}}{\partial x}=\left[ \begin{array}{c} \frac{\partial y_1}{\partial x} \\ \frac{\partial y_2}{\partial x} \\ \vdots \\ \frac{\partial y_m}{\partial x} \end{array} \right]$
此时为正切向量。$\frac{\partial \mathbf{y}}{\partial x}$为$\mathbf{y}$的正切向量。注意，有映射$\mathbf{y}:R^m {\rightarrow } R^m$

3.2 标量关于向量求导

标量$y$关于向量$\mathbf{x}=\left[ \begin{array}{c} x_1\\ x_2 \\ \vdots \\ x_n \end{array} \right]$求导可以表示为$\frac{\partial {y}}{\partial \mathbf{x}}=\left[ \begin{array}{cccc} \frac{\partial y}{\partial x_1} \frac{\partial y}{\partial x_2} \cdots \frac{\partial y}{\partial x_n} \end{array} \right]$
此时为梯度向量。$\frac{\partial {y}}{\partial \mathbf{x}}$为标量$y$在空间$R^m$的梯度，该空间以$\mathbf{x}$为基。

3.3 向量关于向量求导

向量函数（即函数组成的向量）$\mathbf{y}=\left[ \begin{array}{c} y_1\\ y_2 \\ \vdots \\ y_m \end{array} \right]$关于向量$\mathbf{x}=\left[ \begin{array}{c} x_1\\ x_2 \\ \vdots \\ x_n \end{array} \right]$的导数可以写作$\frac{\partial \mathbf{y}}{\partial \mathbf{x}}=\left[ \begin{array}{cccc} \frac{\partial y_1}{\partial x_1} & \frac{\partial y_1}{\partial x_2} & \cdots & \frac{\partial y_1}{\partial x_n} \\ \frac{\partial y_2}{\partial x_1} & \frac{\partial y_2}{\partial x_2} & \cdots & \frac{\partial y_2}{\partial x_n} \\ \vdots & \vdots & \ddots &\vdots \\ \frac{\partial y_m}{\partial x_1} & \frac{\partial y_m}{\partial x_2} & \cdots & \frac{\partial y_m}{\partial x_n} \end{array} \right]$
此时，为Jacobian矩阵

4 关于矩阵的导数

4.1 矩阵关于标量求导

正切矩阵表示为$\frac{\partial \mathbf{Y}}{\partial x}=\left[ \begin{array}{cccc} \frac{\partial y_{11}}{\partial x} & \frac{\partial y_{12}}{\partial x} & \cdots & \frac{\partial y_{1n}}{\partial x} \\ \frac{\partial y_{21}}{\partial x} & \frac{\partial y_{22}}{\partial x} & \cdots & \frac{\partial y_{2n}}{\partial x} \\ \vdots & \vdots & \ddots &\vdots \\ \frac{\partial y_{m1}}{\partial x} & \frac{\partial y_{m2}}{\partial x} & \cdots & \frac{\partial y_{mn}}{\partial x} \end{array} \right]$

4.2 标量关于矩阵求导

梯度矩阵表示为$\frac{\partial y}{\partial \mathbf{X}}=\left[ \begin{array}{cccc} \frac{\partial y}{\partial x_{11}} & \frac{\partial y}{\partial x_{21}} & \cdots & \frac{\partial y}{\partial x_{p1}} \\ \frac{\partial y}{\partial x_{12}} & \frac{\partial y}{\partial x_{22}} & \cdots & \frac{\partial y}{\partial x_{p2}} \\ \vdots & \vdots & \ddots &\vdots \\ \frac{\partial y}{\partial x_{1q}} & \frac{\partial y}{\partial x_{2q}} & \cdots & \frac{\partial y}{\partial x_{pq}} \end{array} \right]$
注意以上$\mathbf{X}$为其索引的转置。

5 布局约定(Layout conventions)

由向量关于向量的求导$\frac{\partial \mathbf{y}}{\partial \mathbf{x}}$可以得出两种矛盾的表示：结果表示为$n \times m$矩阵或$m \times n$矩阵。也就是把$y$表示为列向量$x$表示为行向量或者反过来表示的问题。根据这两种可能，有以下情况：

1. 分子布局(Numerator layout)，即准确表示是$\frac{\partial \mathbf{y}}{\partial \mathbf{x^T}}$（$y$为列向量)，即Jacobian formulation。

2. 分母布局(Denominator layout)，即准确表示是$\frac{\partial \mathbf{y^T}}{\partial \mathbf{x}}$（$y$为行向量)，即Hessian formulation（也有些作者称为梯度布局，尽管梯度不够准确）

所以：

1. 对于分子布局，正切向量$\frac{\partial \mathbf{y}}{\partial x}$为$\mathbf{y}$为列向量，梯度向量$\frac{\partial {y}}{\partial \mathbf{x}}$为行向量。

2. 对于分母布局，正切向量$\frac{\partial \mathbf{y}}{\partial x}$为$\mathbf{y}$为行向量，梯度向量$\frac{\partial {y}}{\partial \mathbf{x}}$为列向量。
3. 对于分子布局，正切矩阵$\frac{\partial \mathbf{Y}}{\partial x}$为$Y$，梯度矩阵$\frac{\partial y}{\partial \mathbf{X}}$为$X^T$
4. 对于分母布局，正切矩阵$\frac{\partial \mathbf{Y}}{\partial x}$为$Y^T$，梯度矩阵$\frac{\partial y}{\partial \mathbf{X}}$为$X$

然而，对于正切矩阵$\frac{\partial \mathbf{Y}}{\partial x}$采用分母布局，即$Y^T$，很不符合表达的习惯,所以一般如下表示：

1. 统一使用分子布局，即$\frac{\partial \mathbf{Y}}{\partial x}$为$Y$，梯度矩阵$\frac{\partial y}{\partial \mathbf{X}}$为$X^T$
2. 使用混合布局，即$\frac{\partial \mathbf{Y}}{\partial x}$为$Y$，梯度矩阵$\frac{\partial y}{\partial \mathbf{X}}$为$X$

注意：

1. 并非所有书与论文从头为都是统一那个分子布局或者分母分的，往往是结合起来使用，根据上下文来确认。
2. 分母布局与分子布局呈转置关系

6 恒等式

由以上可知，计算的结果可以通过转置在分子与分母布局中转换。

以下恒等式基于三条重要法则：求和法则（线性法则）、乘积法则、链式法则（注，类似标量的求导法则得知此三条法则），其中：

1. 求和法则是通用的。
2. 乘积法则对以下讨论大部分情况适用。由于矩阵乘法是不可交换的，所以需要给定矩阵相乘的顺序。标量关于矩阵求导不能直接使用。
3. 链式法则只适用于部分情况。不适用与矩阵关于标量求导即标量关于矩阵求导。后者大部分情况涉及秩的计算。

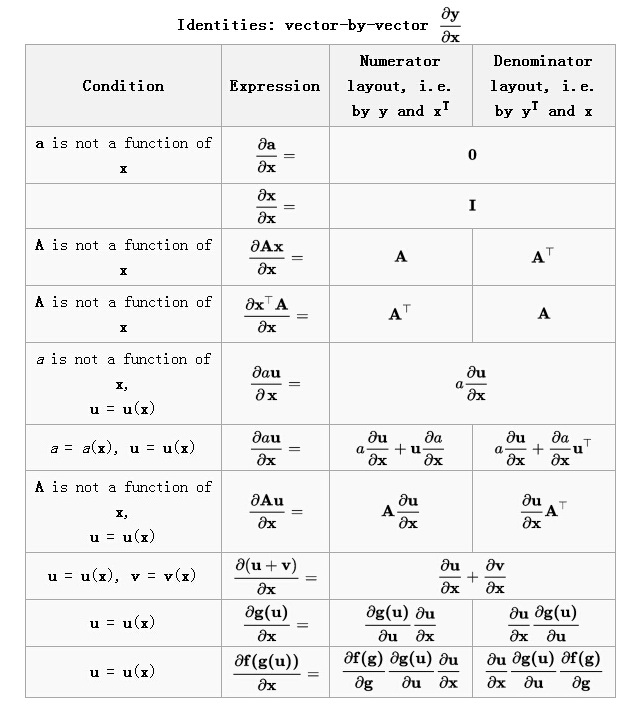
6.1 向量关于向量求导

向量关于标量求导以及标量关于向量求导都可以看出是这种情况的特殊形式。

对于$\frac{\partial \mathbf{y}}{\partial \mathbf{x}}$，有如下恒等：

为说明以上图中分子布局及分母布局中$\mathbf{y}$，$\mathbf{x}$的行列向量表示，把上图中部分项重新详细展开表示，可以有：

条件	表示(未带布局信息)	分子布局	分母布局
$\mathbf{a}$非$\mathbf{x}$的函数	$\frac{\partial \mathbf{a}}{\partial \mathbf{x}}$	$\frac{\partial \mathbf{a}}{\partial \mathbf{x^T}}=\mathbf{0}$	$\frac{\partial \mathbf{a^T}}{\partial \mathbf{x}}=\mathbf{0}$
	$\frac{\partial \mathbf{x}}{\partial \mathbf{x}}$	$\frac{\partial \mathbf{x}}{\partial \mathbf{x^T}}=\mathbf{I}$	$\frac{\partial \mathbf{x^T}}{\partial \mathbf{x}}=\mathbf{I}$
$\mathbf{A}$非$\mathbf{x}$的函数	$\frac{\partial \mathbf{Ax}}{\partial \mathbf{x}}$	$\frac{\partial \mathbf{Ax}}{\partial \mathbf{x^T}}=\mathbf{A}$	$\frac{\partial \mathbf{(Ax)^T}}{\partial \mathbf{x}}=\frac{\partial \mathbf{(x^TA^T)}}{\partial \mathbf{x}}=\mathbf{A^T}$
$\mathbf{A}$非$\mathbf{x}$的函数	$\frac{\partial \mathbf{x^TA}}{\partial \mathbf{x}}$	$\frac{\partial \mathbf{(x^TA)^T}}{\partial \mathbf{x^T}}=\frac{\partial \mathbf{A^Tx}}{\partial \mathbf{x^T}}=\mathbf{A^T}$	$\frac{\partial \mathbf{x^TA}}{\partial \mathbf{x}}=\mathbf{A}$
$a$非$\mathbf{x}$的函数,$\mathbf{u=u(x)}$	$\frac{\partial a\mathbf{u}}{\partial \mathbf{x}}$	$\frac{\partial a\mathbf{u}}{\partial \mathbf{x^T}}=a\frac{\partial \mathbf{u}}{\partial \mathbf{x^T}}$	$\frac{\partial a\mathbf{u^T}}{\partial \mathbf{x}}=a\frac{\partial \mathbf{u^T}}{\partial \mathbf{x}}$

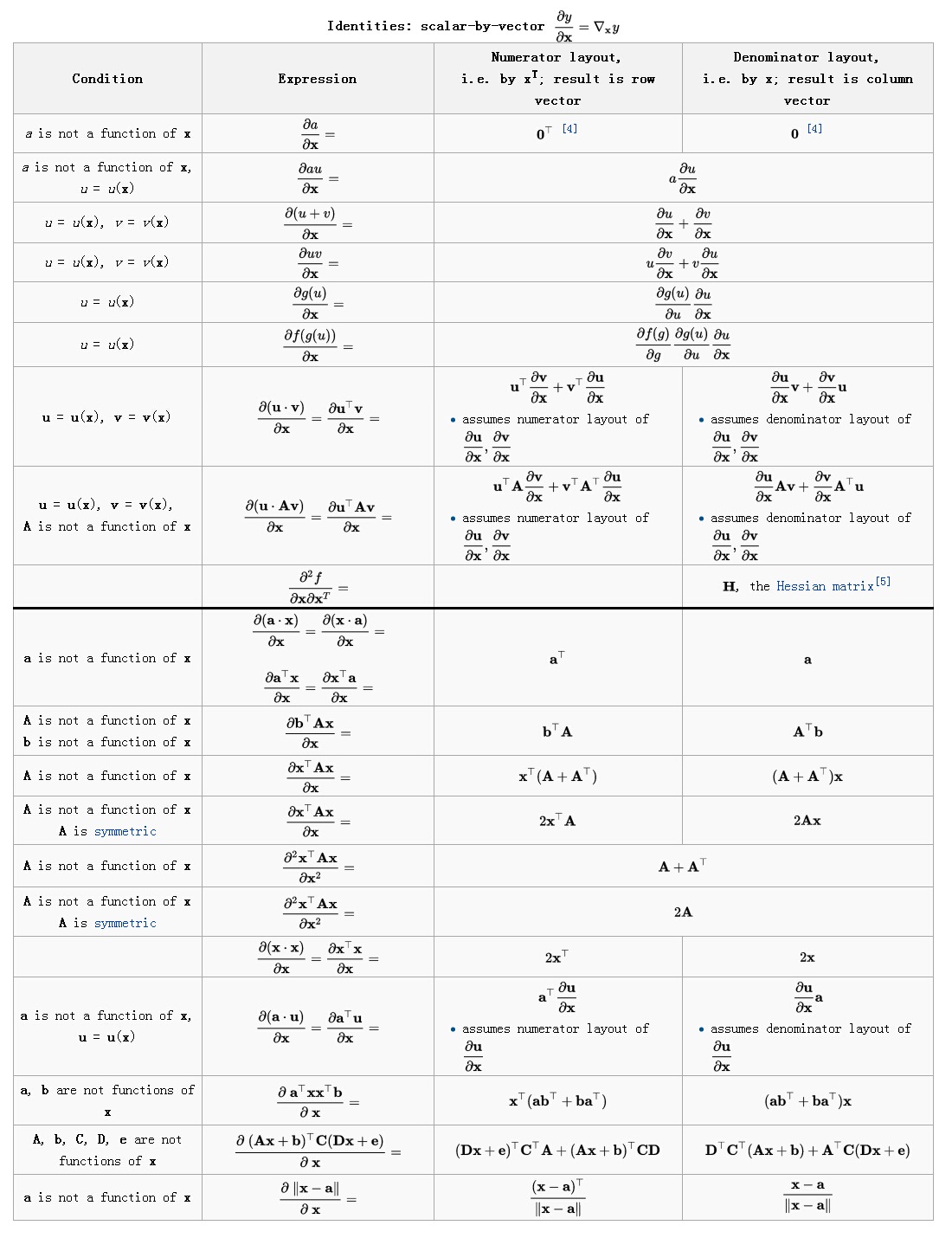
6.2 标量关于向量求导

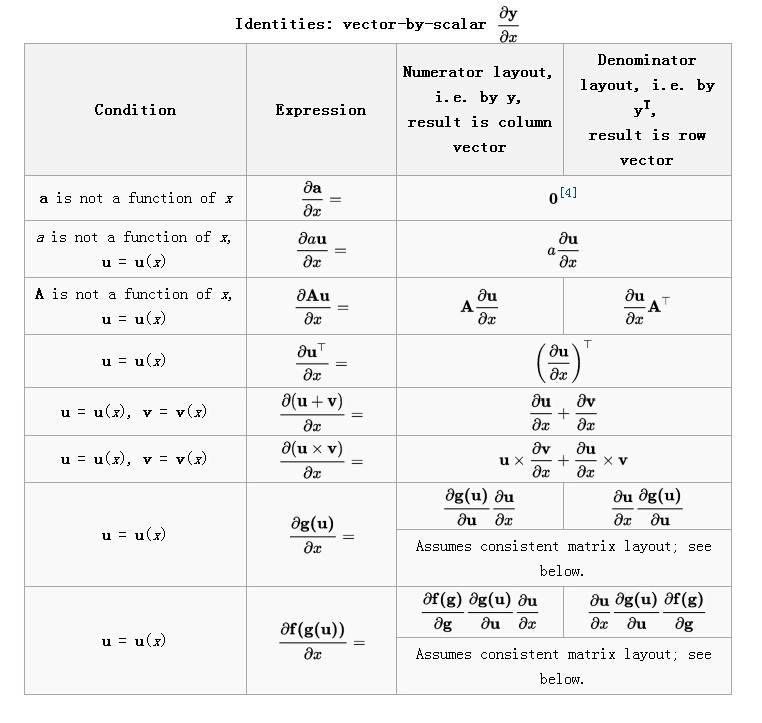
6.3 向量关于标量求导

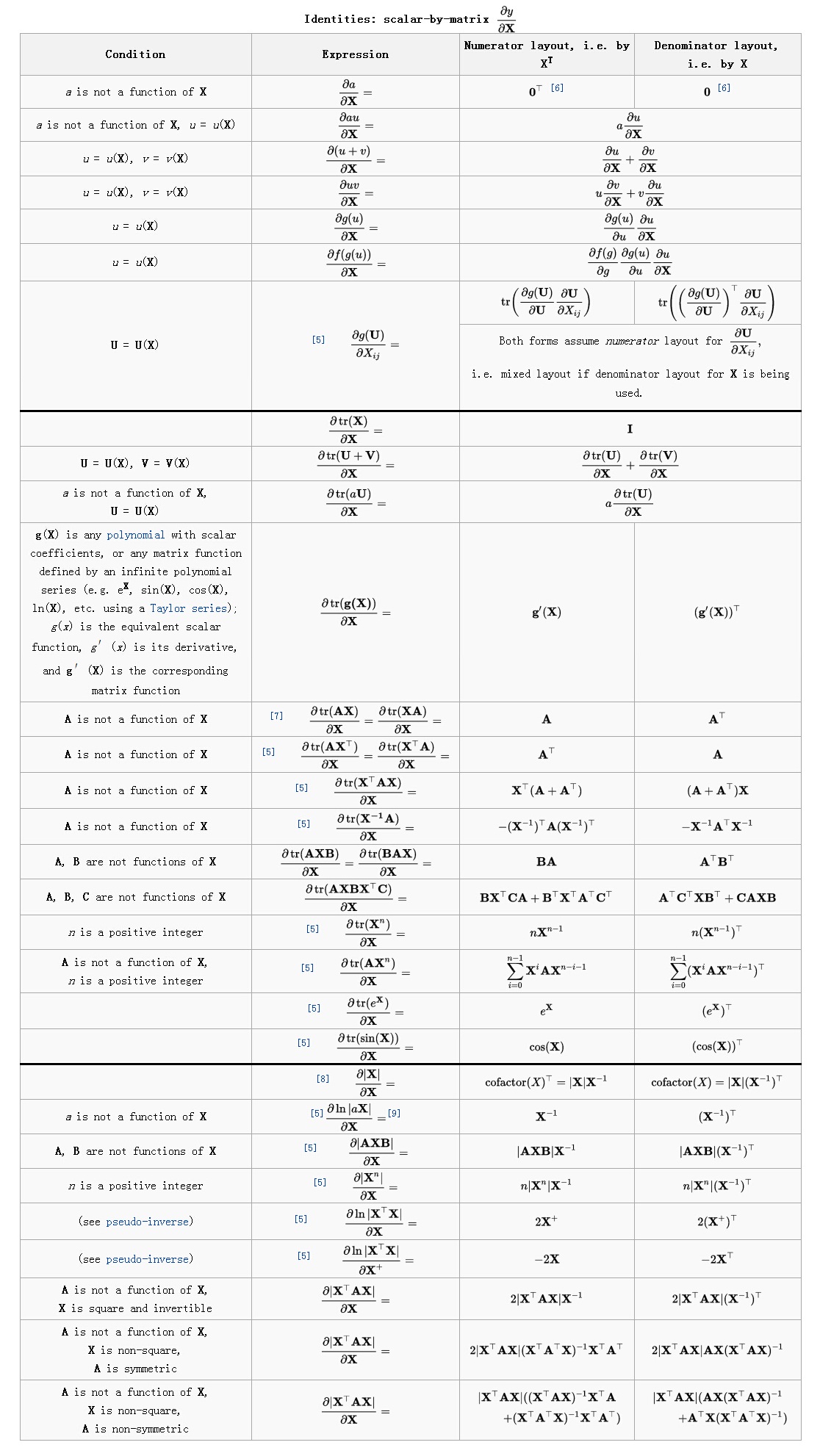
6.4 标量关于矩阵求导

注意此处不适用链式及乘积法则。乘积法则可以借助微分及迹函数的性质得到，因为迹函数转置和循环排列：$tr(A)=tr(A^T)$，$tr(ABCD)=tr(BCDA)=tr(CDAB)=tr(DABC)$。
根据这些性质，如计算$\frac{\partial tr(AXBX^TC)}{\partial X}$：

根据6.7中内容可以得到

6.5 矩阵关于标量求导

6.6 标量关于标量求导

1. 涉及向量
   

2. 涉及矩阵
   

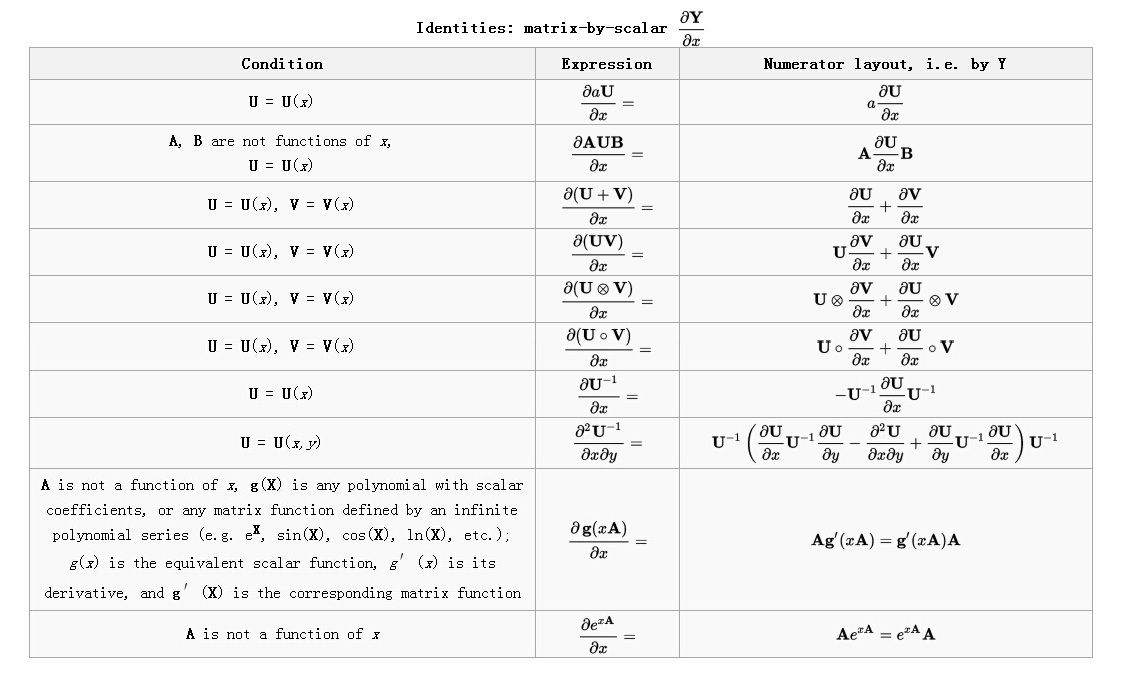
6.7 微分形式

我们常常使用微分形式计算，最后转换成导数形式。仅在分子布局有用，以下”$a$”为标量

1. 标量关于矩阵
   

2. 矩阵
   

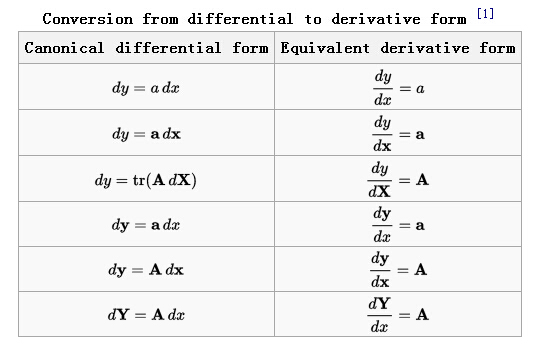
3. 微分到导数转换
   从微分到导数的转换，首先转换成规范形式，然后按照一下等式转换。
   

8 矩阵角度看映射，函数

函数为一对一的关系，可以理解为输入为$n$维，$n\in N^*$，输出为$1$维。进一步可以理解为，输入为$n$维向量，输出为标量。
映射为一对多的关系，可以理解为输入为$n$维，$n\in N^*$，输出$m$维，$m\in N^*$。进一步可以理解为，输入为$n$维向量，输出为$m$维向量。
当然，有时也称呼以上函数为标量函数，映射为向量函数（即由多个标量函数组成映射）