ZOJ3537 - Cake

Cake

---

Time Limit: 1 Second       Memory Limit: 32768 KB

---

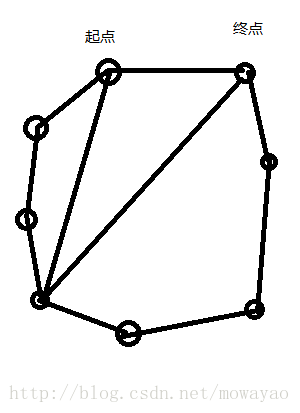
You want to hold a party. Here's a polygon-shaped cake on the table. You'd like to cut the cake into several triangle-shaped parts for the invited comers. You have a knife to cut. The trace of each cut is a line segment, whose two endpoints are two vertices of the polygon. Within the polygon, any two cuts ought to be disjoint. Of course, the situation that only the endpoints of two segments intersect is allowed.

The cake's considered as a coordinate system. You have known the coordinates of vexteces. Each cut has a cost related to the coordinate of the vertex, whose formula is cost_{i, j} = |x_i + x_j| * |y_i + y_j| % p. You want to calculate the minimum cost.

NOTICE: input assures that NO three adjacent vertices on the polygon-shaped cake are in a line. And the cake is not always a convex.

Input

There're multiple cases. There's a blank line between two cases. The first line of each case contains two integers, N and p (3 ≤ N, p ≤ 300), indicating the number of vertices. Each line of the following N lines contains two integers, x and y (-10000 ≤ x, y ≤ 10000), indicating the coordinate of a vertex. You have known that no two vertices are in the same coordinate.

Output

If the cake is not convex polygon-shaped, output "I can't cut.". Otherwise, output the minimum cost.

Sample Input

3 3
0 0
1 1
0 2

Sample Output

0

---

Author:  LI, Zezhou
Contest:  ZOJ Monthly, September 2011

自己把自己坑了好久。。。题目没读清+自认为所给的点即时凸包边上的点。。。。

然后弹了一版

DP方程很简单 一张图就可以解释

看了图瞬间转化为区间DP,当选择了一个顶点的时候，就把区间划分开了

DP[sta][ed] = min(DP[sta][i]+DP[i][ed]+W(sta,i)+W(i,ed)) (sta < i < ed)

我把W的计算看错了。。而且要注意的是当sta == i-1 || ed-1 == i 的时候 W = 0

#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <string>
#include <algorithm>
#include <queue>
using namespace std;
const int maxn = 300+10;
const int INF = 1e9;

struct node{
    int x,y;
    node(int x=0,int y=0):x(x),y(y){}
    friend bool operator <(node a,node b){
        if(a.y!= b.y ) return a.y < b.y;
        else return a.x < b.x;
    }
};
struct polygon{
    vector<node>  P;
    polygon(int Size){
        P.resize(Size);
    }
};

vector<node> vt,vn;
int n,p;
int dp[maxn][maxn];

node operator - (const node &a,const node &b){
    return node(a.x-b.x,a.y-b.y);
}

int det(const node &a,const node &b){
    return a.x * b.y - a.y * b.x;
}

int xmult(node p1,node p2,node p0){

    return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y);
}

int convex_hull(vector<node> p,int n) {

    int i;
    sort(p.begin(),p.end());
    vt[0] = p[0];
    vt[1] = p[1];
    int top = 1;
    for(i = 0;i < n; i++){
        while(top && xmult(vt[top],p[i],vt[top-1]) >= 0)top--;
        vt[++top] = p[i];
    }
    int mid = top;
    for(i = n - 2; i >= 0; i--){

        while(top>mid&&xmult(vt[top],p[i],vt[top-1])>=0)top--;
        vt[++top]=p[i];
    }
    return top;
}

int dfs(int sta,int ed){
    if(ed-sta<=2) return 0;
    if(dp[sta][ed] != -1) return dp[sta][ed];
    int ans = INF;
    for(int i = sta+1; i < ed; i++){
        int d1,d2;
        if(sta+1==i) d1 = 0;
        else d1 = (abs(vt[i].x+vt[sta].x)*abs(vt[i].y+vt[sta].y))%p;
        if(ed-1==i) d2 = 0;
        else d2 = (abs(vt[i].x+vt[ed].x)*abs(vt[i].y+vt[ed].y))%p;
        ans = min(ans,dfs(sta,i)+dfs(i,ed)+d1+d2);
    }
    return dp[sta][ed] = ans;
}

int main(){


    while(cin >> n >> p){
        vn.clear();
        vt.clear();
        vt.resize(maxn);
        vn.resize(n);
        memset(dp,-1,sizeof dp);
        for(int i = 0; i < n; i++) cin >> vn[i].x >> vn[i].y;

        sort(vn.begin(),vn.end());
        if(n<=3){
            cout<<0<<endl;
            continue;
        }
        if(convex_hull(vn,n)!=n){
            cout<<"I can't cut."<<endl;
        }else{
            cout<<dfs(0,n-1)<<endl;
        }

    }
    return 0;
}