【数字逻辑】学习笔记 第五章 Part2 时序逻辑电路(分析与设计)

一、时序逻辑电路分析

1. 同步时序逻辑电路分析

(1) 分析目的

分析时序逻辑电路在输入信号的作用下，其状态和输出信号变化的规律，进而确定电路的逻辑功能。

(2) 分析方法

利用驱动方程、次态方程和输出方程 ， 求出在任何给定的输入变量状态和存储电路状态下时序电路的输出和次态

• 驱动方程：触发器输入端的逻辑表达式
• 次态方程：将驱动方程代入对应触发器特征方程得到的逻辑表达式
• 输出方程 ：时序电路输出信号的逻辑表达式

(3) 分析步骤

1.了解电路的组成：电路的输入、输出信号、触发器的类型等

2.根据给定的时序电路图，写出下列各逻辑方程式：

• 各触发器的驱动方程
• 各触发器的次态方程
• 时序电路的输出方程

3.列出状态转换表或画出状态图和波形图

4.确定电路的逻辑功能

---

2. 例题A

例1：分析以下电路的逻辑功能：

(1) 写方程组

• 输出方程：$z=Q_3^n$
• 驱动方程：
  $$\{\begin{array}{rl}& J_1=\overline{Q_3},K_1=1\\ & J_2=Q_1^n,K_2=Q_1\\ & J_3=Q_1^n{Q}_2^n,K_3=1\end{array}$$
• 次态方程：这是下降沿触发的J-K触发器，因此 $$Q^{n+1}=J\overline{Q^n}+\overline{k}{Q}^n$$

从而，可以得到以下的次态方程组：
$$\{\begin{array}{rl}& Q_1^{n+1}=\overline{Q_3^n}\overline{Q_1^n}\\ & Q_2^{n+1}=Q_1^n\overline{Q_2^n}+\overline{Q_1^n}{Q}_2^n=Q_1^n\oplus Q_2^n\\ & Q_3^{n+1}=Q_1^n{Q}_2^n\overline{Q_3^n}\end{array}$$

(2) 根据方程组列出状态转移真值表

(3) 根据状态转移真值表画状态转移图

(4) 根据状态转移图画时序图

(5) 检查电路能否重启动

检查电路能否从 非工作状态 （未出现在状态转移真值表中的状态） 进入工作状态

非工作状态：$101,110,111$
分别代入次态方程组和输出方程：

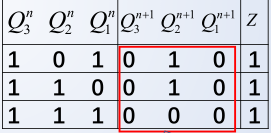
电路可以由非工作状态进入工作状态，故可以自启！

(6) 画出完整的状态图

(7) 判断电路功能

由于时钟脉冲控制状态从 $000-001-010-011-100-000$，循环变换，逢五进一，可知，该电路是一个同步的五进制计数器

3. 例题B

分析以下电路的逻辑功能：

(1) 写方程组

这也是下降沿触发的J-K触发器。

• 输出方程：$Z=(X\oplus Q_2^n)\cdot \overline{Q_1^n}$
• 驱动方程：
  $$\{\begin{array}{r}{J}_1=X\oplus \overline{Q_2^n},K_1=1\\ J_2=X\oplus Q_1^n,K_2=1\end{array}$$
• 次态方程：$Q^{n+1}=J\overline{Q^n}+\overline{K}{Q}^n$

可得次态方程组：
$$\{\begin{array}{r}{Q}_1^{n+1}=(X\oplus \overline{Q_2^n})\overline{Q_1^n}\\ Q_2^{n+1}=(X\oplus Q_1^n)\overline{Q_2^n}\end{array}$$

(2) 列状态转移真值表

① 当 $X=0$ 时，化简方程：
$$\{\begin{array}{rl}& Q_1^{n+1}=(X\oplus \overline{Q_2^n})\overline{Q_1^n}=\overline{Q_2^n}\overline{Q_1^n}\\ & Q_2^{n+1}=(X\oplus Q_1^n)\overline{Q_2^n}=Q_1^n\overline{Q_2^n}\\ & Z=Q_2^n\overline{Q_1^n}\end{array}$$

② 当 $X=1$ 时，化简方程：
{