频繁项集挖掘算法——H-mine算法

       前面我们已经介绍了4种频繁项集挖掘算法，有经典的，也有比较新提出的，现在我们再来学习一种比较新的频繁项集挖掘算法——H-mine算法。

         前面已经提到FP-growth 将挖掘长频繁模式的问题转换为递归地搜索较短模式，然后连接后缀。该算法使用最不频繁的项作为后缀，提供了较好的选择性，使用该算法大大的降低了搜索开销。但是当数据量非常大时，构造基于内存的FP 树是非常困难的。

        传统频繁模式挖掘算法主要存在两个问题：一是算法需要的内存大小是不可预测的并且当数据集规模增大时，需要的内存也会随之剧增；二是在很多情况下算法效率是非常低或无法处理的，如密集型数据集、海量数据集。

        主要思想

        H-mine 算法一定程度上解决了上面提到的问题。H-mine是一种基于内存、高效的频繁模式挖掘算法，使用新的数据结构H-Struct，可以更快的遍历数据。理论上，H-mine 有多项式的空间复杂度，要比使用候选产生发现频繁项集和频繁模式增长方法更加节约空间。H-mine 通过对数据进行分区，每次只挖掘一个分区最后将结果整合，极大的节约了内存并能处理更大规模数据集。实验证明H-mine 算法有极好的可扩展性并且在任何情况下综合性能都优于Apriori 算法和FP-growth 算法。                                                         

        方法描述

        同样地，为了让大家更好地理解该算法，我们也通过一个实例来说明H-mine算法的挖掘过程。

        下表1的前面两列是我们的示例事务数据库TDB。假设最小支持度计数为min_sup=2。

                                                            表1 示例事务数据库TDB

                        

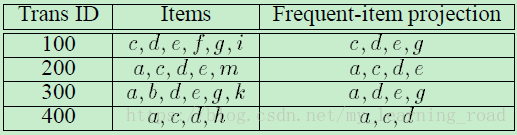
        与Apriori算法相同，首先扫描TDB一遍，找到并输出频繁1项集｛a：3，c：3，d：4，e：3，g：2｝，这里a：3表示项a的支持度计数为3。用freq(X)表示项集X（每个X对应每一个事务数据库）中的一组频繁项，也就是X的频繁项投影。每个事务的频繁项投影如表1第3列所示，比如TID=100的事务，它原来的项为c，d，e，f，g，i，但是f和i均不为频繁项，所以TID=100的事务的频繁项投影为c，d，e，g。其他的以此类推。

        根据字母顺序将频繁项排列（称为F-list）：a-c-d-e-g，那么我们最后想要得到的完整的频繁模式被分成5个子集：（1）那些包含项a的；（2）那些包含项c但是不包含项a的；（3）那些包含项d但是不包含项a也不包含项c的；（4）那些包含项e但是不包含项a、项c和项d的；（5）那些仅仅包含项g的。

        根据上述的频繁项投影可以得到H-struct，如图1所示：所有在频繁项投影中的项都根据F-list排序。例如T100的频繁项投影被列为cdeg，每一个频繁项的item-id和hyper-link（指针）都被存储在H-struct中。

                                        

                                                                            图1  H-struct

        Header table H中有3个域࿱