2024高教社杯数学建模竞赛A题B题C题D题E题完整成品文章和全部问题的解题代码更新

2024高教社杯数学建模竞赛A题B题C题D题E题完整成品文章和全部问题的解题代码完整版本更新如下：https://www.yuque.com/u42168770/qv6z0d/rytbc1nelty1mu4o

要知道国赛的国奖不是按照比例来给的，每年国赛国一ABC题每题固定100个队左右，所以选的人越少越容易获奖！

推荐大家选A题冲奖，获奖机会大，而且推荐国奖不容易被刷，去年我们赛区A题推荐国奖没有一个被刷，B题刷了将近25%国奖，C题刷了15%以上国奖。本人打了20余场比赛，国赛和美赛做的都是A题，拿了21国赛国一，22美赛的F，今年我又带队参加24年的数学建模国赛了

很多人觉得A题难，其实A题只是看起来难，其实也有很多套路。下面我就来分享一下我的A题建模经验。

2024数学建模国赛常见模型汇总

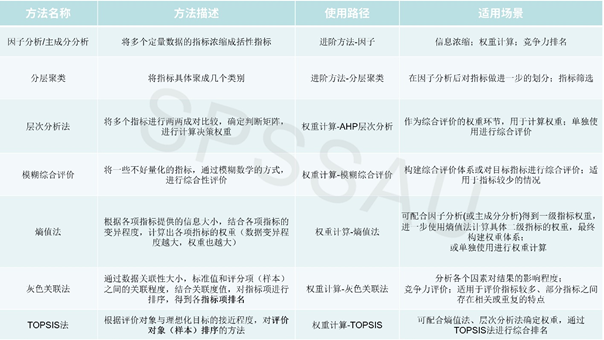
2024年高教社杯数学建模国赛各种评价方法的适用条件

国赛做题套路

不管是A题B题C题，优化问题是国赛和美赛中最重要也是最常见的问题，基本上大部分模型都可以建成优化模型，所以，优化问题需要重点关注

不管是国赛还是美赛，优化模型都可以分成外部的优化模型和内部的具体模型

外部模型目标函数：（，，，）控制方程（内部模型）：（，，）约束条件：；；；初始条件：；；；外部模型{目标函数：minS=G（a，b，x，y）控制方程（内部模型）：y=F（a，b，x）约束条件：a；b；x；y初始条件：a；b；x；y

第一问建模方法

分析过去5年的国赛A题，第一问几乎都是参数优化问题，一般会给附件数据，我们把它抽象出来，也就是需要先建立一个模型，通过附件数据拟合模型中的未定参数。

首先，什么是参数优化？举个例子，对于模型y=f(x)=ax+b，附件中会给定x和y的值。当然，模型y=ax+b不会告诉你，这是自己建立的模型。建立了模型之后，通过数据去拟合，求解参数a和b

怎么求a和b，这就是关于算法的问题。对于y=ax+b这样简单的模型，拟合本质上是优化，我们可以使用各种成熟的优化算法，如：单步长（变步长）搜索法、二分搜索法、黄金分割搜索法、最小二乘法、遗传粒子群模拟退火算法

以下是2021国赛训练做的2020国赛A题炉温曲线的第一问的参数拟合求解

第二、三问建模方法

第二、三问是正问题和反问题的优化求解。通过建立的模型和标定好的参数，将模型中的某些变量作为自变量，再将这些量作为若干个优化目标函数的自变量，求解目标函数对应的解。

这里的目标函数可能是以下几种情况，函数关系式记为F：

1. 模型中的参数或者参数的函数关系式，比如a，b，或者F（a；b）

2. 模型的自变量或者自变量的函数关系式，比如x，或者F（x）

3. 模型的因变量或者因变量的函数关系式，比如y，或者F（y）

4. 关于模型中的若干个变量的函数关系式，比如F(a；b；x；y)

注意上面的a，b，x，y可以推广为向量或者矩阵形式，a=[a1,a2,a3...an]；b=[b1,b2,b3...bn];x=[x11,x12,x13,...x1n;x21,x22,x23,...x2n;...;xn1,xn2,xn3...,xnn]

同时，参数a，b也可以分为恒定参数和可变参数。例如2020A题中，各温区的温度（[T1-5, T6, T7, T8-9]）和过炉速度（v）是可变参数，热传导因子( )是恒定参数，()已经由第一问拟合得到。

上面第1、2种情况是反问题，第3种情况是正问题，第4种情况是正反问题的结合

以y=ax+b为例，第一问已经建立好了y=ax+b这个模型，并且根据附件数据求解了最优的参数a和b的值。现在，整个模型已经确定。第二问的目标函数的自变量为y；x；a；b，目标函数的因变量（记为y2），y2=f（y，x，a，b），求解使得y2最优的（y、x、a，b）的其中一个或者某几个。

以2020A题为例，问题二给出了各温区温度的设定值，其中小温区1-5 为182ºC，小温区6 为203ºC，小温区7 为237ºC、小温区89为254ºC，需要求解在满足制程界限的前提下，允许的最大传送带过炉速度。对应到上面的y=ax+b的模型，目标函数量是传送带过炉速度v，其中v是模型中的参数，即符合第一种情况

问题3需要求解[T1-5, T6, T7, T8-9, v]，使得超过217ºC 到峰值温度所覆盖的面积最小。这里的优化自变量是[T1-5, T6, T7, T8-9, v]，这些都是模型中的参数，目标函数面积S是温度曲线的函数，温度曲线可以由参数[T1-5, T6, T7, T8-9, v]和自变量（时间t）等通过模型推导得到。因此这一问的目标函数是第四种情况，即F(a；b；x；y)

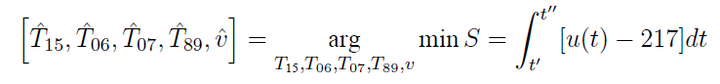
添加图片注释，不超过 140 字（可选）

问题4的是多目标函数，面积S最小化和对称性指标D最小化。同第三问，目标函数是第四种情况

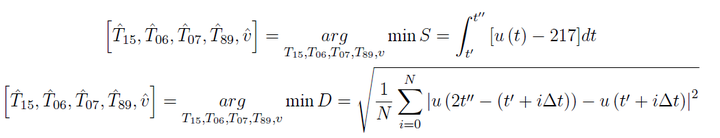
如何判别是否是优化问题

1. 凡事关于最小最大相关或者尽量相关的词汇，一般都是优化问题。收益最大，风险最小，尽量对称，尽量小，尽量大等等

2. 另外还有一种最后趋于稳定的问题，一般也是优化问题，例如2019A高压油管压力控制，油压最后稳定在100，优化目标是最后一秒的油压曲线与100的偏差最小

优化问题的组成部分

注意优化问题特别是微分方程问题，一般由5个主要部分构成，它们分别是：

1. 优化变量（自变量）

2. 优化目标（单目标、多目标）（因变量）

3. 控制方程（微分方程模型主体及其他附属方程）

4. 边界条件

5. 初始条件

在论文写作时，我们需要做的是把优化目标、控制方程、约束条件等用数学语言表达出来。需要注意：应该明确写出上面5个部分，如果某些部分没有，应该至少写出优化目标和控制方程

以我们2021国赛暑期训练为例，我们做的是2020国赛A题炉温曲线，各位可以自行阅读题目，此处不赘述题目

模型的建立部分

在写作时，明确写出以xx为优化变量、以xx为控制方程（约束条件）、以xx为优化目标的单目标（多目标）优化模型

上面写完了模型的引入，下面开始写模型的公式：

其中优化变量和优化目标可以写一起，举例如下。其中排第一位的是优化变量的估计，表示求解出来的值只是全局最优的估计；argmin（argmax）下标优化变量，表示使得后面的优化目标方程最小时的优化变量的精确值；最后是优化目标方程

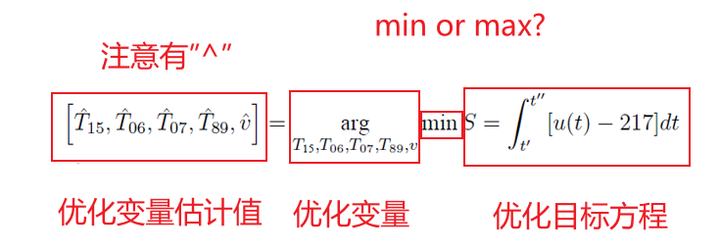
上面的是单目标的写法，对于多目标优化，写法也一样，如下：

下面开始写控制方程以及约束，注意有下面两点。

第一点、使用大括号把控制方程和约束条件、边界条件写一起。

第二点、后面需要有变量符号的解释（其中，a为：，b为：...）

为什么要这么写？原因是这样评委一看就知道所有的东西，一目了然！

当然，你也可以将上面5个部分分开写，我2022美赛A题就是这样写的，如下，也就是每个部分写个小标题并加粗：

第一、决策变量（优化变量)）

第二、目标方程（优化目标）

第三、控制方程

第四、约束条件

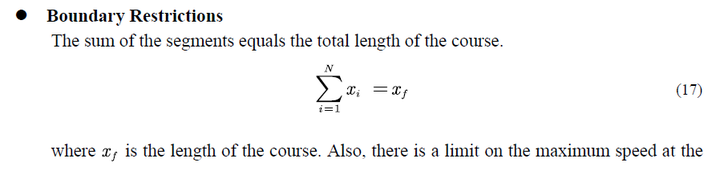
第五、初始条件

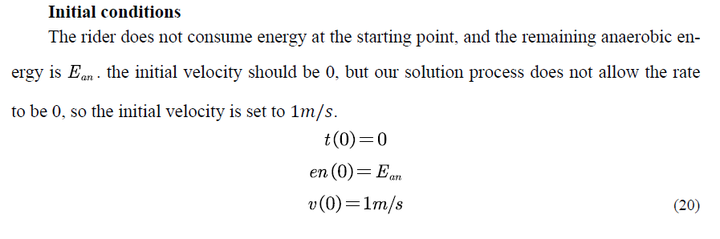
不管是国赛还是美赛，优化模型都可以分成外部的优化模型和内部的具体模型

下面将外部模型的求解和内部模型的求解分开讲述，首先是外部优化模型的求解：

外部优化模型的求解

上面建立完了模型，我们就开始写模型的求解，这部分就是算法了

对于一个优化问题，如何选择算法？当然算法不是乱选的，你得体现你的思考与创新

比如对于一个参数搜索问题，变步长搜索就比单步长搜索要好，为什么？因为变步长搜索在趋于最优解的时候缩小步长，能够减少运算次数，这就是它的优点。

再进一步，二分搜索法比变步长搜索法更好。你用二分，别人用穷举搜索，你的算法就比别人的更优秀。

注意，不是越复杂的算法就越好，而是使用简单的算法在最短的时间内解决问题才是最优的算法。

下面是一些常见优化问题的求解算法

参数拟合或者参数标定问题

利用最小二乘法，优化目标是误差最小，拟合函数一般是复杂的常微分方程(2019A)或者偏微分方程(2020A，2018A)，例如2020A题需要拟合带10个未知参数的偏微分方程，这时候就需要用遗传算法等智能算法了

求复杂函数的最小\最大值\零点

1. 求解最大最小值一般，先用变范围搜索的方法大致搜索一遍，然后:

2. 对于单调函数，用二分法

3. 对太复杂的，一般用智能算法

内部具体模型的求解

1. 求解常微分方程（组）的方法有欧拉法，改进欧拉法，龙格库塔法，算法最好自己写，尽量不调库。例子：2019A高温油管压力控制

2. 求解偏微分方程（组）一般是有限差分法，一般需要自己写算法。例子：2018A高温服装设计、2020A炉温曲线

3. 多变量、多约束优化问题求解，使用罚函数法，例子：2021A题FAST反射面节点调节

常微分方程的求解

为了编程时更好的与我们外部优化模型的迭代算法匹配，常微分方程我们一般使用手写的改进欧拉法代码迭代求解。

利用欧拉法求解微分方程 ，将时间等分，区间长度是h， ，则 ，精度为O(h)。

利用改进欧拉法求解微分方程 ，将时间等分，区间长度是h， ，则 ，精度为O(h2)。

利用改进欧拉法求解混合微分方程 ，将时间等分，区间长度是h， 。则y1的迭代公式为 ，y2的迭代公式为

微分方程组求解要点：

• 因变量个数与方程个数相同

• 尽量使用最基础的理论（牛顿第二定理等）

• 只采用一阶微分方程组的形式

• 尽量采用向量方式处理

• 尽量做到可进行数组运算（并行计算， 存贮空间换时间）

• 如无法理论求解，不做化简（只做计算机数值计算）

• 保留混合微分方程的形式

1.建立混合微分方程的函数代码，（对复杂的微分方程组往往比较困难）

2.利用库函数求解（精度满足条件），或用欧拉、改进欧拉自编程求解（时间换精度）

在无法理论求解的情况下，高阶理论往往只有理论上的优势，对数值求解帮助不大，基础理论形式更简洁明了

以2019年A题高压油管控制为例，第一问建立的模型如下：

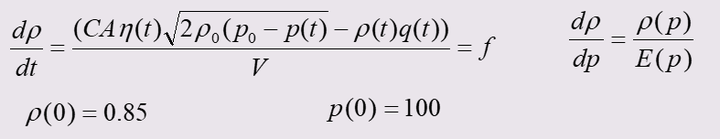
取定参数a, T，将时间等分，区间长度是h，初始化： ，根据改进欧拉法，由 计算 。依次循环计算下去，可得所有时间节点的压力及密度值

编程的代码如下：

function [p,t]=f(time,T,p1)  %time 总时长， T 开阀时间
    global p0 A C V
    h=0.001; n=floor(time*1000/h)+1; a=0;
    t=(0:n-1)*h;       %时间列
    p=zeros(n,1);      %对应的压强
    midu=zeros(n,1);   %对应的密度
    rho0=dens(p0); p(1)=p1;  midu(1)=dens(p1);
    tmp1=h*C*A*eta(t,a,T)*sqrt(2*rho0)/V;
    tmp2=h*q(t)/V;
     %改进欧拉法迭代求解
    for i=1:n-1
        tmp=tmp1(i)*sqrt(p0-p(i))-midu(i)*tmp2(i);
        midu(i+1)=midu(i)+tmp;
        p(i+1)=p(i)+tmp*sc(p(i))/midu(i);
    end
end

第二问建立的模型如下，求解方法同理：

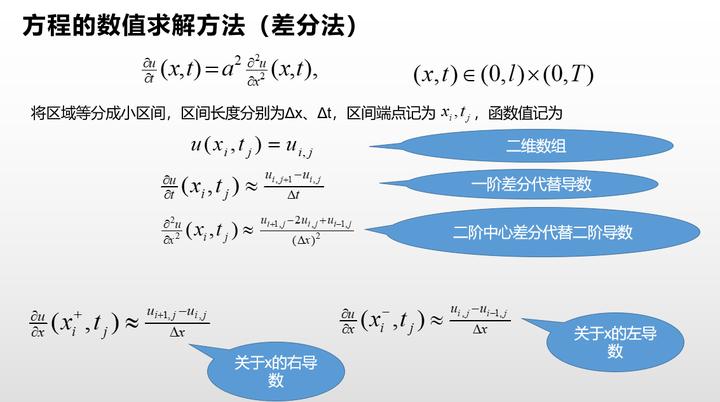
偏微分方程的求解

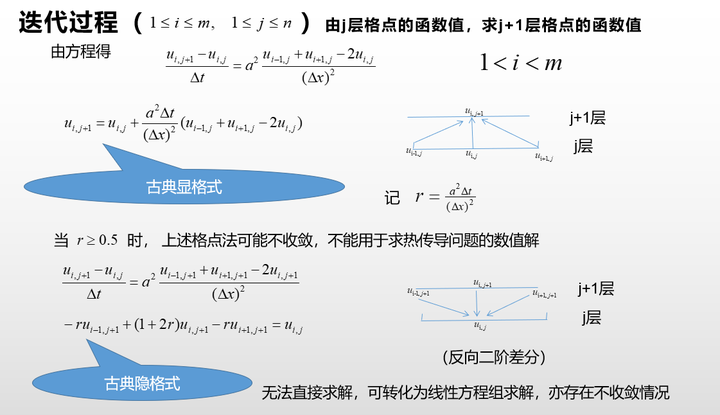
偏微分方程的求解使用有限差分法，有前向差分、后项差分、CN隐格式差分。使用差分法的时候，需要考虑稳定性和收敛性的问题。Crank-Nicolson 隐格式收敛性与稳定性都优于古典显格式和古典隐格式。

同时，需要明确是第几类边界条件！！选错边界条件类型，直接全盘出错！！！

以热方程的求解为例（2018A题高温服装设计）：

添加图片注释，不超过 140 字（可选）

添加图片注释，不超过 140 字（可选）

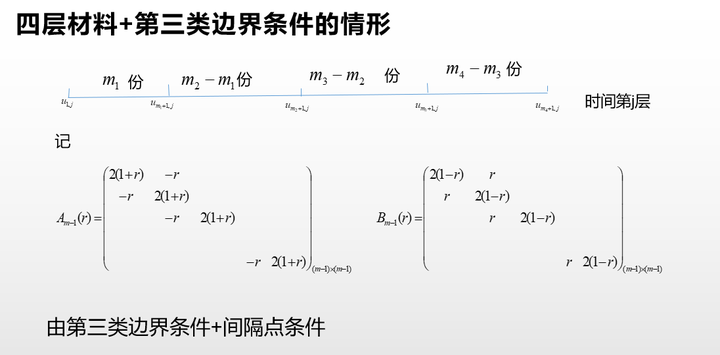
建立好模型之后，编程求解也不是很困难，核心就是3个矩阵：

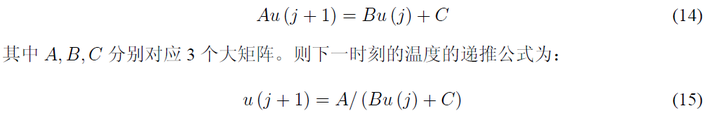
多变量、多约束优化问题求解 （罚函数法）

对于多变量、多约束优化问题： ，转化为新无约束优化问题， 。

求解步骤如下：

1. 令x1=x0，计算 ，如果 ，跳到3，否则2

2. 找 ，设最小点为 ，令k=k+1,

3. 计算等式、不等式平方和及|x0-x1|, 若最大值<esp, 结束，否则 1

其中esp为误差精度； 为初始点，初始取k=1

要点：

1. 多变量、无约束优化问题有很多算法，选合适的

2. 变量太多，粒子群、遗传、蚁群等算法应该不适应

3. 要注意用向量并行计算，避免循环语句

以2021A题FAST节点调节为例，建立以下模型：

部分求解代码如下

while tol>eps
     x1=x0;
     while 1
        y0=dfun(x0)+c*(dineq(x0)+deqf(x0));
        tmp=norm(y0);
        if tmp<eps
           break;
        end
        h=-y0/tmp;
        fhandle=@(t) fun(x0+t*h)+c*(ineq(x0+t*h)+eqf(x0+t*h));
        range=max(tmp,range);
        [t,g0]=funm(fhandle,range);
        range=t*50;
        g1=fun(x0);
        g2=ineq(x0);
        g3=eqf(x0);
        x0=x0+t*h;
    end
    if c>1e8
        break;
    else
        c=r*c;
    end
    tol=max([err1,err2,err3]); 
end



function y=dineq(x)                    %x(n,4) 主索节点坐标及促动器伸缩量
%y 不等式约束在x的梯度值
global side_ind_square index           
r=0.0007;                               % 边长最大容许伸缩比
E=x(:,1:3);                             % 主索节点坐标
s=x(:,4);                               %促动器伸长量
y=zeros(size(x));
tmp=E(side_ind_square(:,1),:)-E(side_ind_square(:,2),:);
tmp1=sum(tmp.*tmp,2);
tmp2=tmp1-side_ind_square(:,3)*(1+r)^2;
tmp3=side_ind_square(:,3)*(1-r)^2-tmp1;
tmp2=max(0,tmp2);
tmp3=max(0,tmp3);
tmp4=4*(tmp2-tmp3).*tmp;
tmp5=max(0,s.^2-0.36);
y(:,1:3)=index*tmp4;
y(:,4)=4*s.*tmp5;
end

function g=ineq(x)                    %x(n,4) 主索节点坐标及促动器伸缩量
%g 不等式约束在x值
global side_ind_square err1 err3 
r=0.0007;                               % 边长最大容许伸缩比
E=x(:,1:3);                             % 主索节点坐标
s=x(:,4);                               %促动器伸长量
tmp=E(side_ind_square(:,1),:)-E(side_ind_square(:,2),:);
tmp1=sum(tmp.*tmp,2);
tmp2=tmp1-side_ind_square(:,3)*(1+r)^2;
tmp3=side_ind_square(:,3)*(1-r)^2-tmp1;
tmp2=max(0,tmp2);
tmp3=max(0,tmp3);
tmp4=max(0,s.^2-0.36);
g=sum(tmp2.^2)+sum(tmp3.^2)+sum(tmp4.^2);
err3=max(tmp4/0.72);
err1=max(max(tmp2,tmp3)./side_ind_square(:,3));
end

function g=eqf(x)       %x(n,4) 主索节点坐标及促动器伸缩量
%g 等式约束在x值
global L l P e err2                       
E=x(:,1:3);                       % 主索节点坐标
s=x(:,4);                         %促动器伸长量
tmp=P-E+e(:,1:3).*(L+s);
tmp1=sum(tmp.*tmp,2)-l;
t1=tmp1.^2;
g=sum(t1);
err2=max(abs(tmp1)./l)/2;
end

function y=deqf(x)       %x(n,4) 主索节点坐标及促动器伸缩量
%y 等式约束在x的梯度值
global L l P e                       
E=x(:,1:3);                       % 主索节点坐标
s=x(:,4);                         %促动器伸长量
y=zeros(size(x));
tmp=P-E+e(:,1:3).*(L+s);
tmp1=sum(tmp.*tmp,2)-l;
tmp2=sum((P-E).*e,2);
y(:,1:3)=4*tmp1.*(E-P-(L+s).*e);
y(:,4)=4*tmp1.*(L+s+tmp2);
end

function g=fun(x)                  %x(n,4) 主索节点坐标及促动器伸缩量
%g 优化函数在x值
global k R p
f=0.466*R;                       
s=-0.3361;
F=f-s;                    %焦距
E=x(k,1:3);  
tmp=sum(E.^2,2);
tmp1=E(:,1:3)*p';
tmp2=tmp1.^2;
tmp3=tmp-tmp2-4*F*(tmp1-s+R);
g=tmp3'*tmp3;
end

function y=dfun(x)                  %x(n,4) 主索节点坐标及促动器伸缩量
%y 优化函数在x的梯度值
global k R p
f=0.466*R;                       
s=-0.3361;
F=f-s;                    %焦距
y=zeros(size(x));
E=x(k,1:3);  
tmp=sum(E.^2,2);
tmp1=E(:,1:3)*p';
tmp2=tmp1.^2;
tmp3=tmp-tmp2-4*F*(tmp1-s+R);
y(k,1:3)=4*tmp3.*(E-tmp1*p-2*F*ones(length(k),1)*p);
end