卡尔曼滤波（Kalman Filter）深入解析：从零开始彻底搞懂预测与修正（适合小白，无需数学基础，一步步深入讲解）

室内定位小白

已于 2025-03-13 19:49:30 修改

阅读量3.8k

点赞数 55

分类专栏：室内定位及涉及算法文章标签：算法

于 2025-03-13 18:14:11 首次发布

本文链接：https://blog.csdn.net/navsense_support/article/details/146231513

版权

室内定位及涉及算法专栏收录该内容

6 篇文章

订阅专栏

在昨天的文章中，我复盘了 均值滤波（滑动平均滤波）、中值滤波、指数滤波、高斯滤波 这些基本滤波方法。这些方法虽然简单易用，但在 复杂环境下（如高噪声、动态系统） 可能存在不足。它们有一个共同的问题：

只能基于过去的数据进行简单的平滑处理，但无法预测未来。
无法区分真实信号和噪声，一旦数据波动较大，它们可能会使信号失真。

今天，我将复盘更高级的滤波方法：卡尔曼滤波（Kalman Filter，KF），它的核心特点是：

✅ 能够预测数据的未来趋势 ${x}_{k}^{ }$
✅ 结合当前数据进行修正，使预测更加准确
✅ 可以处理动态变化的系统，比如目标跟踪、导航定位等
✅ 能够区分信号和噪声，即使数据被干扰，依然能估计出真实值

在查看网上各种关于卡尔曼滤波的资料时，发现几乎都是通过数学模型带领大家了解学习，因此我在考虑如果通过简单直白的方式，让我同组并没有平差基础的学弟学妹了解卡尔曼滤波，所以下面我会用尽量简单、直白的话语和例子来解释和介绍卡尔曼滤波。

1.卡尔曼滤波的核心思想

卡尔曼滤波的思想其实很简单，就是 不断进行“预测”和“修正”：

预测：基于之前的数据，估算当前的值。
修正：用传感器或测量数据，对预测值进行调整，使其更加准确。
重复上述步骤，不断优化，使误差越来越小。

2.状态变量（State Variables）是什么

在卡尔曼滤波中，我们用一个状态变量 ${x}_{k}^{ }$ 来描述系统的状态。
比如，在定位问题中，状态变量可能包含：

仅位置：
位置 + 速度：
位置 + 速度 + 加速度：

卡尔曼滤波的目标就是估计状态变量 ${x}_{k}^{ }$

3.下面结合实际，来简单的讲述卡尔曼滤波的公式：

假设一个汽车：

当前在 5 米 的位置。
速度是 2 米/秒。
你想预测它1 秒后的位置。

那么：预测位置=5+2=7 米

这就是卡尔曼滤波的预测阶段： $\hat{x}_k^-=A\hat{x}_{k-1}+Bu_k$

$\hat{x}_k^-$ ：预测的状态，在这个情景下表示为

A: 状态转移矩阵，描述状态如何从上一个时刻 k−1 变化到当前时刻 k。（例如速度的影响）

（可以把状态转移矩阵 A理解为一个“时间推进器”，它决定了当前状态如何变化到下一时刻。

例如：

表示：1. 新位置 = 旧位置 + 速度 × 时间 2. 速度保持不变

B：控制输入对状态的影响程度（控制矩阵）

$u_{k}$ ：控制输入（Control Input），表示 外部施加的影响，例如 加速、刹车、方向调整等。如果没有外部输入，B $u_{k}$ 这部分可以忽略。

以上就是你预测汽车位置的一个过程，这在卡尔曼滤波中被定义为：预测阶段（Prediction Step），但是现实世界并不是完美的，测量数据会受到噪声影响，所以就还有接下来的过程，被称作修正阶段（Correction Step）

如果你用测距仪器（有误差）发现汽车的位置是 6.5 米，而预测是 7 米，你会怎么办？

👉 你不会完全相信预测值（速度或者位置是有一定偏差的不是确定的5米初始位置和确定的2米/s的速度），也不会完全相信测量值（因为测量值也有误差），而是取一个折中值！取折中值的方式就是其实就是取一个权重

这个过程称为修正（Correction）：

$\hat{x}_k = K_k \cdot z_k + (1 - K_k) \cdot \hat{x}_k^-$

也可以写成：

$\hat{x}_k=\hat{x}_k^-+K_k\left(z_k-\hat{x}_k^-\right)$

$z_{k}$ ：测量值（用测量仪测的距离是6.5 米）

$\hat{x}_{k}^{-}$ ：预测值（你自己算出来是7米）

$K_{k}$ ：卡尔曼增益，决定如何在预测和测量之间取折中。其实就相当于一个权重：如果测量值很可靠（传感器误差很小），那么 $K_{k}$ 取较大值，我们更相信测量值。如果测量值噪声较大，那么 $K_{k}$ 取较小值，我们更依赖预测值。

比如我们让 $K_{k}$ =0.75（假设我们认为传感器测量较准确，但也不是说非常非常非常准）

按照公式：汽车真实的位置 $\hat{x}_k$ =0.75⋅6.5+0.25⋅7=6.625 米

上面就是最简单的卡尔曼滤波的过程。

我们刚刚讲的例子里，测量值 $z_{k}$ 和状态变量 $\hat{x}_{k}^{-}$ 都是位置，所以直接做加权平均即可。但如果测量的不是位置，而是速度，我们该怎么办？

这时候，我们需要引入 观测矩阵 H！

$\hat{x}_k=\hat{x}_k^-+K_k\left(z_k-H\hat{x}_k^-\right)$

在某些情况中，我们的状态变量不仅仅是位置，还可能包括速度、加速度等多个变量。例如：

但我们的测量设备可能只能测量其中一部分信息，测量值只有速度，我们不能直接做加权平均，而是要从状态变量中提取出速度信息。那么H矩阵在这时候就定为：

那么

（由于测量值仅包含速度，而状态变量同时包含位置和速度，因此我们通过矩阵 HHH 提取状态变量中对应的速度信息，以确保修正过程仅影响速度，而不会改变位置。）

这样，我们就能正确计算修正值：

这就是矩阵 H的作用：只让测量到的部分进行修正，不会影响其他状态变量。

以上就是简单的卡尔曼滤波理解了，简单来说，就是先根据上一时刻状态进行预测，然后结合测量值进行修正，不断优化估计结果。

但是理解了以上的过程，也只是刚刚入门卡尔曼滤波的流程，真正的理解卡尔曼滤波，还需要掌握以下几个关键点：

B 矩阵是什么？
$u_{k}$  代表什么？
卡尔曼增益 $K_{k}$  的计算过程

4.B 矩阵与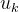 $u_{k}$ 是什么？

B 描述控制输入 $u_{k}$ 如何影响状态，不同的系统有不同的 B 形式。

还是刚刚那个汽车直线运动的例子，在这个例子中，状态变量为

在没有外部控制输入的情况下，状态转移方程为： $\hat{x}_k^-=Ax_{k-1}$

其中： $A= \begin{bmatrix} 1 & t \\ 0 & 1 \end{bmatrix}$

也就是说： $\hat{x}_k^-= \begin{bmatrix} 1 & t \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x_{k-1} \\ v_{k-1} \end{bmatrix}$

表示：

新位置 = 旧位置 + 速度 × 时间（x=x0+v0t）。
速度保持不变（如果没有加速度作用）。

如果汽车受到了加速度 a的作用，那么：

物理规律：

位置变化： $x=x_{0}+v_{0}t+\frac{1}{2}at^{2}$
速度变化： $v=v_0+at$

那么：

$B= \begin{bmatrix} \frac{1}{2}t^2 \\ t \end{bmatrix},\quad u_k=a$

所以控制输入对状态变量的影响：

$Bu_k= \begin{bmatrix} \frac{1}{2}t^2 \\ t \end{bmatrix}a$

最终的完整状态预测公式：

$\hat{x}_k^-= \begin{bmatrix} 1 & t \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x_{k-1} \\ v_{k-1} \end{bmatrix}+ \begin{bmatrix} \frac{1}{2}t^2 \\ t \end{bmatrix}a$

这表示：

如果没有外部控制，那么状态仅由 AA 矩阵决定（惯性运动）。
如果有外部控制，那么加速度会影响位置和速度，并通过 B 矩阵建模。

✅状态预测 = 惯性运动（ $Ax_{k-1}$ ） + 控制输入（ $Bu_{k}$ ）。
✅ 如果没有外部控制， $u_{k}$ =0，状态完全由 A 预测。
✅ 如果有加速度 a，那么 $Bu_{k}$ 让加速度影响位置和速度，状态预测更加精准！

5.卡尔曼增益 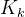$K_{k}$ 的计算过程

在卡尔曼滤波的修正阶段，我们希望在预测值和测量值之间取一个最佳的折中。

如果测量值很可靠（误差很小），那么我们更应该信任测量值。
如果测量值误差较大，那么我们应该更依赖预测值。

计算 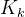$K_{k}$ 之前，先理解“误差”

在卡尔曼滤波中，我们不仅要估计状态（如位置），还要估计这个状态的误差大小。

我们用误差协方差矩阵 $p_{k}$ 来衡量估计的可信度：

如果 $p_{k}$ 很大，说明我们的预测值不太可信，误差较大。
如果 $p_{k}$ 很小，说明我们的预测值很可靠，误差较小。

此外，测量值 $z_{k}$ 也有误差，我们用测量噪声协方差 R来衡量测量值的可信度：

如果 R 很小，说明测量值很准确。
如果 R 很大，说明测量值噪声较大，我们应该更依赖预测值。

为了让估计值更准确，我们希望：

如果 预测值不确定性大（ $p_{k}$ 很大），那么 $K_{k}$  变大，更多依赖测量值 $z_{k}$ 。
如果 测量值不确定性大（R 很大），那么 $K_{k}$ 变小，更多依赖预测值 $\hat{x}_k^{-}$ 。

这个权重的计算公式如下：

$K_k=P_k^-H^T(HP_k^-H^T+R)^{-1}$

看到这个公式，感觉已经不想学了是吧.....（我刚学到的时候也是：这什么xx东西!）

先不要被公式吓到，我们分步拆解它的意义。（当你有耐心看到这里的时候，你已经无敌了）

首先，我们把这个公式里所有的符号代表的意思整理一下：

$K_{k}$ ：这个叫卡尔曼增益，它是我们在进行估计修正（也就是预测修正过程）时用的权重值。
简单来说，就是用来决定我们到底更相信预测值，还是更相信测量值的。
$p_{k}$ ：这个是预测状态的误差协方差矩阵，反映了预测结果（刚刚我们通过起始位置和速度预测出的小车位置）的不确定性。
简单理解：
- 如果预测越不确定（误差越大），则这个矩阵越“大”。
- 如果预测越准确（误差越小），则这个矩阵越“小”。
H：这个叫做测量矩阵，用来把预测状态（比如位置、速度这些东西）变换成测量空间中的值。
通常 H 会告诉我们，“实际测量到的数据”和“预测的状态”之间是怎样一种关系。
R：这个是测量噪声协方差矩阵，表示我们测量值中误差（用测距仪器得到的汽车位置）的不确定性。
- 如果测量值越准确（误差越小），则 R 越“小”。
- 如果测量值越不准（误差越大），则 R 越“大”。
上标T（ $H^{T}$ ）：代表矩阵转置，简单来说，就是把原来矩阵的行和列交换位置
上标-1：代表矩阵求逆，我们把它看作类似于除法运算的概念，理解为它能“消除”矩阵的作用。

好了接下来我们解释公式中的：

我们有一个预测的结果（例如：你猜测自己走路去了某个位置，但你不确定你是否猜准了），我们要知道这个预测有多大的误差这个误差到底有多大呢？我们把预测的误差表示为 $P_k^{-}$ 。但是，预测误差通常是表示状态的（比如：位置、速度），而我们测量到的值不一定是位置和速度本身，比如可能只是距离或某个间接的测量量。

此时我们需要一个东西，把预测误差从状态空间（例如位置）“映射”或“换算”到 测量空间（你实际测量到的距离）里去。

这个“换算工具”，就是我们说的 H 矩阵。用更简单的话理解：

$P_k^{-}$ 是告诉你：“我位置可能不准了”
乘以 H，变成了 $HP_{k}^{-}H^{T}$ ，意思就变成了：“假如位置不准了，那么我这个测量值（比如距离）会不准到什么程度？”

这一步本质上在衡量：“预测状态的不确定性”会导致测量空间里的误差到底有多大。

我们测量得到的数据本身也有误差，叫 R。测量本身也会带来不确定性（仪器不准、噪声干扰等）

所以，我们把预测带来的测量空间误差 $HP_{k}^{-}H^{T}$ 和测量本身的误差 R 相加：

$HP_k^-H^T+R$

这个式子告诉你：“如果我同时考虑预测和测量的不确定性，整体误差到底有多大？”

好了，现在我们知道了两个误差：

预测的不确定性（在测量空间）： $P_k^{-}H^T$
总的误差（预测不确定性+测量误差）： $(HP_{k}^{-}H^{T}+R)$

接下来，我们就想知道：

在总的误差里面，预测误差到底占了多大的比重？

用数学表达就是用 $P_k^{-}H^T$ 除以这个总误差 $(HP_{k}^{-}H^{T}+R)$ ，得到比例，也就是卡尔曼增益：

$K_k=P_k^-H^T(HP_k^-H^T+R)^{-1}$

那么现在就是如何计算 $P_k^{-}$ 和R了

我们已经知道了：

$P_k^{-}$ 表示的是预测状态的误差协方差矩阵（预测误差）。
R表示的是测量误差协方差矩阵（测量误差）。

接下来我们一个一个详细看：

（一）如何计算 $P_k^{-}$ ？

它的计算公式如下： $P_k^-=F_kP_{k-1}F_k^T+Q_k$

别慌，我们再慢慢解释公式中的每个字母：

$P_k^{-}$ ：当前时刻（k 时刻）预测的误差协方差矩阵
：状态转移矩阵（State Transition Matrix），简单理解就是告诉你：“状态是怎么从上一步变化到这一步的？”（类比于最上面公式的A）
- 比如汽车从上一秒的位置到这一秒的位置，会根据速度发生变化， $F_{k}$ 就是描述这种变化关系的矩阵。
$P_{k-1}$ ：上一时刻（k−1时刻）的误差协方差矩阵（上一步你已经算出来了）。
$Q_{k}$ ：过程噪声协方差矩阵，。表示的是过程噪声 $w_{k}$ 的方差：