K-means聚类分析及SPSS实现

1.概述

k均值聚类算法（k-means clustering algorithm）是一种迭代求解的聚类分析算法，其步骤是，预将数据分为K组，则随机选取K个对象作为初始的聚类中心，然后计算每个对象与各个种子聚类中心之间的距离，把每个对象分配给距离它最近的聚类中心。聚类中心以及分配给它们的对象就代表一个聚类。每分配一个样本，聚类的聚类中心会根据聚类中现有的对象被重新计算。这个过程将不断重复直到满足某个终止条件。终止条件可以是没有（或最小数目）对象被重新分配给不同的聚类，没有（或最小数目）聚类中心再发生变化，误差平方和局部最小。

2.计算步骤

（1）初始化：随机选择k个中心点，作为初始的聚类中心。
（2）计算距离：计算每个样本到k个中心点的距离，将各样本划分到距离最近的中心点所在的簇。
（3）重新计算中心：为各簇所有点的均值，重新计算各簇的中心。
（4）迭代：不断迭代2、3步骤，直到各簇不再发生变化或者达到预设的迭代次数。

3.优缺点

K-Means聚类算法的优点包括：
(1)原理简单，实现容易，收敛速度快。
(2)聚类效果较优，能够将簇紧凑，使得簇内相似度高。
(3)算法的可解释度较强。
(4)只需调整k值，即可得到不同数量的聚类结果。
K-Means聚类算法也存在以下缺点：
(1)K值的选取不好把握，通常需要通过实验和可视化方法来确定合适的K值。
(2)对于初值的选择敏感，不同的初值会导致不同的聚类结果。为了克服这个问题，可以采用k-means++算法来选择初始中心点。
(3)对于非凸形状的簇、大小和密度不同的簇，K-Means算法容易受到离群点的影响，导致聚类效果不佳。这时可以考虑使用基于密度的聚类算法，如DBSCAN算法。
(4)只能收敛到局部最小值，而不能找到全局最小值。因此，在应用K-Means算法时，需要多次运行，并选择效果最好的结果。

4.SPSS实现步骤

本文取人口数据依据人口综合情况对各省份进行分类，数据来源国家统计局。
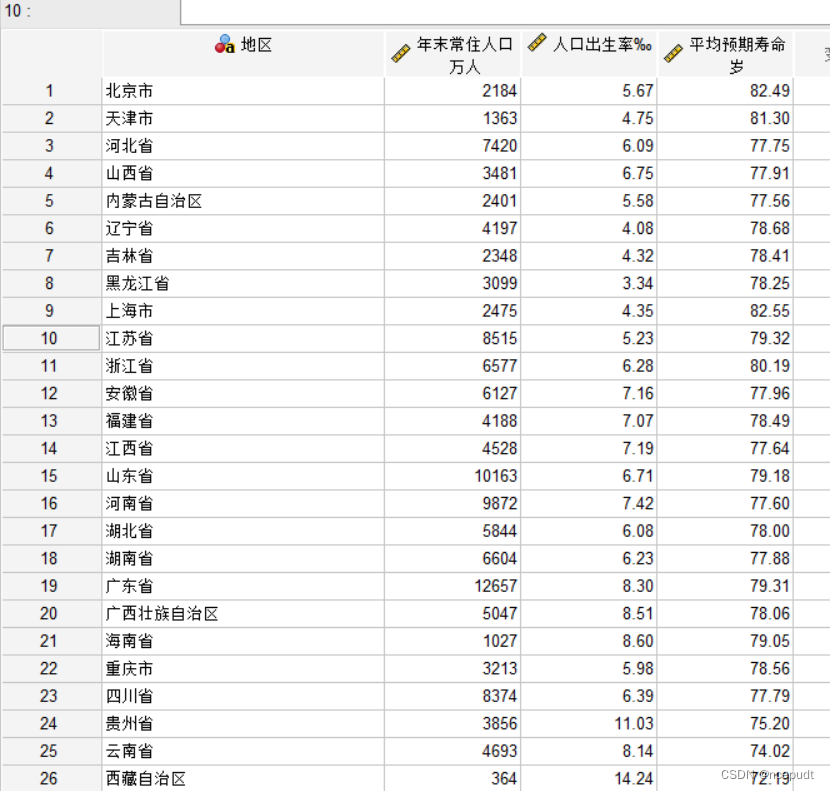各省份历年人口数据
4.1.数据标准化处理
Z-score标准化（也叫标准分数）：这是最常见的标准化方法，它将每个观测值转换为平均数为0，标准差为1的标准正态分布。公式是：
Z = (X - μ) / σ
其中，X是原始数值，μ是均值，σ是标准差。依据标准化处理规则，对数据进行标准化处理。
【1】分析——描述统计——描述

【2】弹出“描述统计”对话框，首先将准备标准化的变量移入变量组中，此时，最重要的一步就是勾选“将标准化得分另存为变量”，最后点击确定。

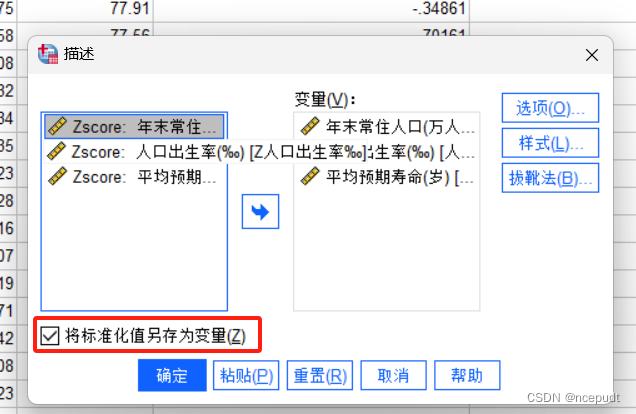
【3】返回SPSS的“数据视图”，在原始变量的最后多了一列Z开头的新变量，这个变量就是标准化后的变量了。基于此字段继续开展分析。

4.2.k-means聚类
【1】选择“分析-分类-k-均值聚类”

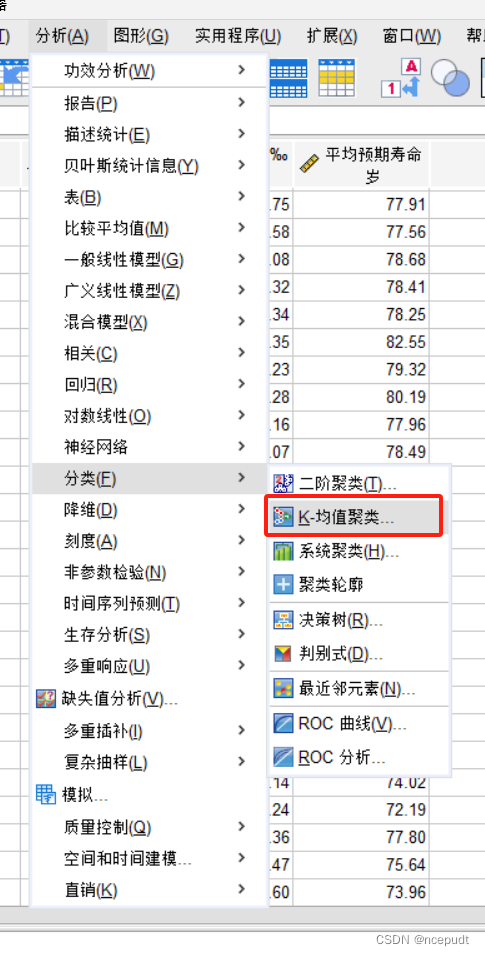
【2】变量选择标准化后的变量，依据选择地区，最大迭代次数选择10次

【3】结果解读


上图表示分成2类的分类结果，即北京、天津等25个城市为一类，贵州等6个城市为一类，但是ANOVA表中年末常住人口显著性大于0.05，效果不好。所以将分类数调成3类再分析。


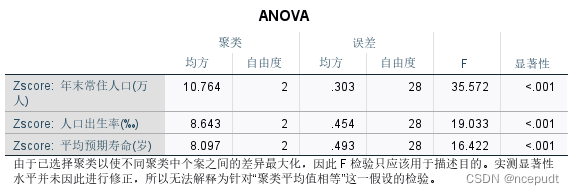
上图表示分成3类的分类结果，即北京、天津等16个城市为一类，贵州、云南等6个城市为一类，河北、山东等9城市为一类。其中聚类均方对应组间均方差，误差均方对应组内均方差，显著性p<0.05时说明此变量分类效果好。由表可知，大部分变量的p<0.05,且组间均方差大于组内均方差，说明各变量在三个类别中的差异大，分类结果可信度高。