2016年湖南省第十二届大学生计算机程序设计竞赛 解题报告

这次省赛居然出题方居然不是刘汝佳而是换成了叉姐，现场上看到ICPCCAMP这几个字的时候我的内心是血崩的/(ㄒoㄒ)/~~。不过说实话，叉姐的题，有毒!，吸的我根本停不下来~

先发个做题地址：题目

再放一个大牛的一句话题解：别人的题解

反正题面大部分都是中文，我就不描述题意了（葛优躺）

Problem A: 2016

解法1：对于一个数a，可以表示成（a/2016*2016+a%2016）的形式，那么a和b相乘是否为2016的倍数只需看右边模的部分。于是只需把所有模数的个数算出来就ok了，复杂度：2016^2。

解法2：在现场写的解法，假设我知道了一个数a，那么与a相乘能为2016的倍数的b的个数为m/(2016/gcd(a,2016))。显然枚举a是不现实的，那么我们可以尝试取枚举gcd(a,2016)=k，然后看能满足的a有多少个，由于k的枚举量不超过2016，可行，那么如何求gcd(a,2016)=k的合法数呢。假如k=1的时候，相当于求n以内有多少个数与2016互素，这个容斥一下便能解决。然后对于gcd(a,2016)=2的合法数，等价于求gcd(a/2,2016/2)=1，即n/2以内与1008互素的个数，其余同理。然后我们就求出了gcd(a,2016)=k的a的个数，乘上对应的b的个数，枚举k并累加起来便是答案。复杂度：非常快

Problem B:有向无环图
观察式子count(i,j)*a[i]*b[j]，对于一个点j来说，对答案的贡献可以表示成（∑count(i,j)*a[i]）*b[j]。动手画一画可以发现（∑count(i,j)*a[i]）是具有传递性和累加性的。我们令dp[u]表示u点上的（∑count(i,u)*a[i]），那么u点对于答案的贡献为dp[u]*b[u]，对于一个u连接的点v，dp[u]对dp[v]的贡献为dp[u]+a[u]。然后对着图的拓扑序进行dp即可

Problem C:Three Capitals

解法1：从1号点出发，遍历每条边一次后回到1号点，人们称之为欧拉回路，那么这题实际上就是欧拉回路计数了，这个时候有个名为BEST theorem的定理可以求得。该定理表示一个有向图的欧拉回路数其中tw(G)=以w为根的树形图的个数，deg(v)为点v的出度数，其中tw(G)在一般情况下需要matrix-tree定理求得，不过这题的顶点只有3个，以1为根的树形图的数目手算都能算出来所以不需要matrix-tree定理（树形图是指在图上选择一些边使图上所有节点形成一颗树，不同的边组成的树形图也算不同）。由于BEST定理是有向图的，根据欧拉回路的性质，每个顶点的出度=入度，我们可以枚举从1号点指向2号点的边数量，从而给整张图定向。最后我们把所有的欧拉回路算出来后乘上点1的出度数便是答案。

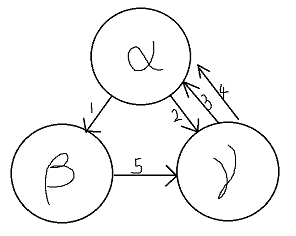
这里为何要乘上1的出度呢，要注意欧拉回路是无始无终的，以下图为例

可以看到下面两种边走的方式1->5->3->2->4和2->3->4->1->5是同属于一种欧拉回路的，所以对于每一种欧拉回路我们有deg(1)种不同方式

代码：

<span style="font-size:14px;"><span style="font-size:10px;">#include <stdio.h>
#include <algorithm>
#include <set>
#include <string.h>
#include <math.h>
#include <iostream>
#include <vector>
#include <map>
#include <queue>
#define fi first
#define se second
using namespace std;
typedef long long ll;
typedef pair<int, int> PII;
const int inf = 0x3f3f3f3f;
const double eps = 1e-8;
const int mod = 1e9 + 7;
const int maxn = 100000 + 10;

ll f[maxn];
void init() {
	f[0] = 1;
	for (int i = 1; i < maxn; ++i) {
		f[i] = f[i - 1] * i % mod;
	}
}

ll mypow(ll a, ll b) {
	ll ans = 1;
	while (b) {
		if (b & 1) ans = ans * a % mod;
		b >>= 1;
		a = a * a % mod;
	}
	return ans;
}

ll inv(ll x) {
	return mypow(x, mod - 2);
}

ll C(int n, int m) {
	return f[n] * inv(f[n - m]) % mod * inv(f[m]) % mod;
}

int main() {
#ifndef ONLINE_JUDGE
	freopen("test.in", "r", stdin);
#endif
	
	init();
	
	int a, b, c;
	while (~scanf("%d%d%d", &a, &b, &c)) {
		if ((a + b) % 2 || (b + c) % 2 || (a + c) % 2) {
			puts("0");
			continue;
		}
		int dega = (a + b) / 2, degb = (a + c) / 2, degc = (b + c) / 2;
		
		ll ans = 0;
		ll ab, ac, ba, bc, ca, cb;
		for (int i = 0; i <= a; i++) {
			ab = i;
			ba = a - ab;
			ac = dega - ab;
			ca = b - ac;
			bc = degb - ba;
			cb = c - bc;
			if (ab >= 0 && ac >= 0 && ba >