曲线积分小结

写在开头

两类曲线积分的联系和区别

第一类和第二类曲线积分的区别就是理论和应用的区别。

第二类曲线积分是给第一类曲线积分赋予物理意义后的形式，所以是由第一类定义的第二类（从名字也能看出是先有一后有的二）。有点像数学家先定义了第一类曲线积分，然后被物理学家看到了，觉得哎你这理论跟我研究的规律之间有点联系，于是拿过来改吧改吧，就有了第二类曲线积分。

那么这个跟第一类曲线积分有联系的物理规律是什么？没错，就是做功。

在做功的情景下，第一类和第二类曲线积分的区别可以解释为：第一类是以路径S为基准，只分解力F，然后计算S上的分力和S的乘积W，最后积分；而第二类是以xy轴为基准，同时分解力F和路径S，然后分别计算x轴上的分功和y轴上的分功再合并相加算出W，最后积分。（这个基准也就是d后面跟着的变量）

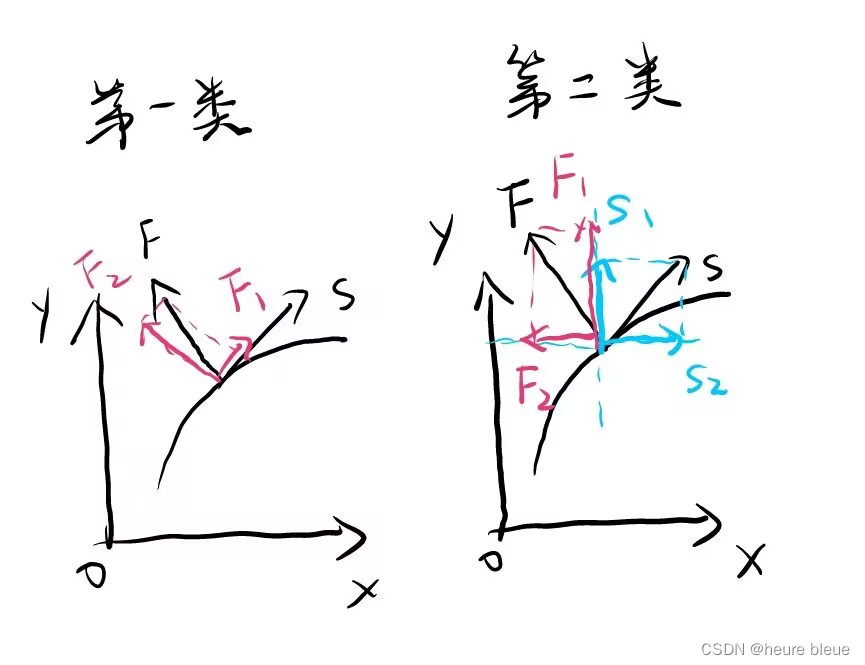
需要注意的是，正常情景下，第一类曲线积分的物理意义是求一条曲线上的质量（也就是被积函数值）累积，只是物理学家进一步把被积函数定义成了功，再进一步分为两个向量的数量积，这才有了做功情景下的第一类曲线积分和随之衍生的第二类曲线积分。

那么由图可知，第一类和第二类之间显然是可以互相转化的。以下是比较完整的推导过程，其中的红框部分就是我们最常用的转化公式。

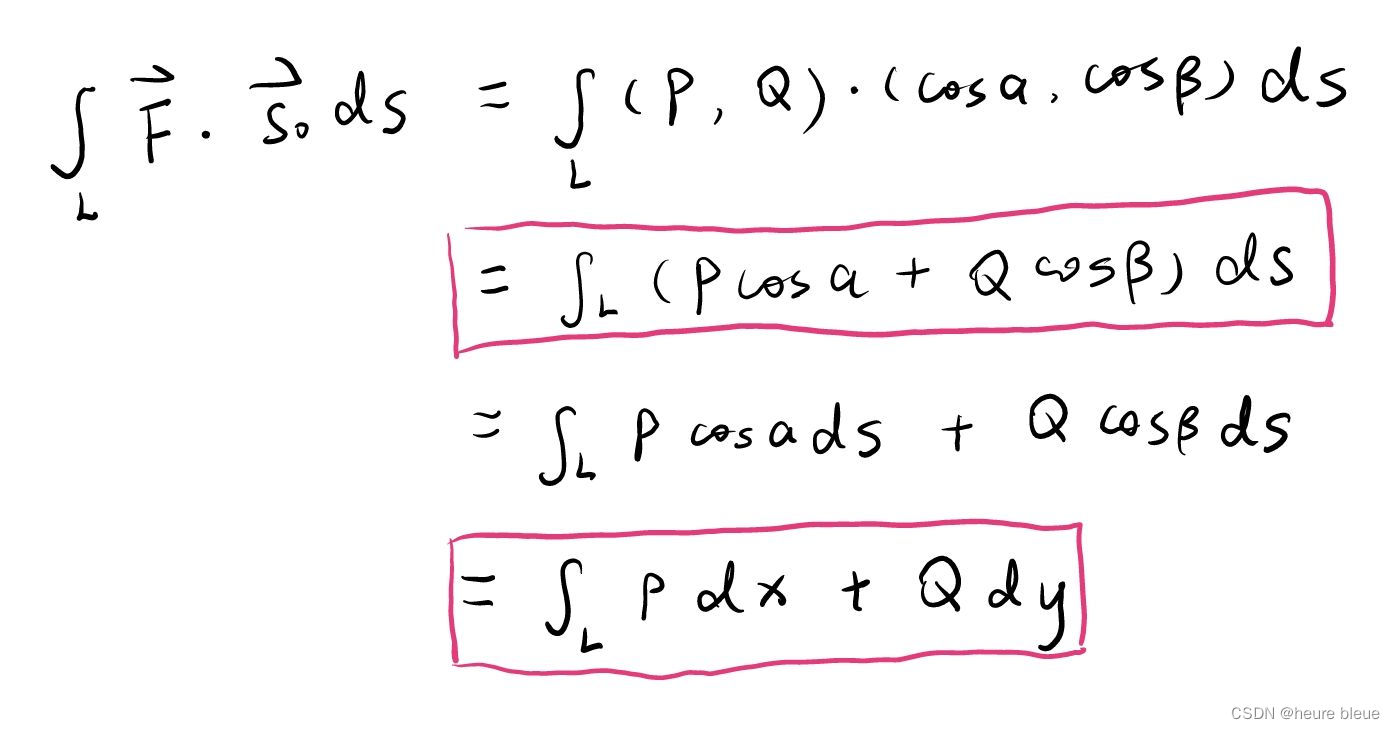
其中方向向量s0（cos，cos）有以下两种形式：

类似的三维曲线方向方向s0（cos，cos，cos）同样有两种形式：

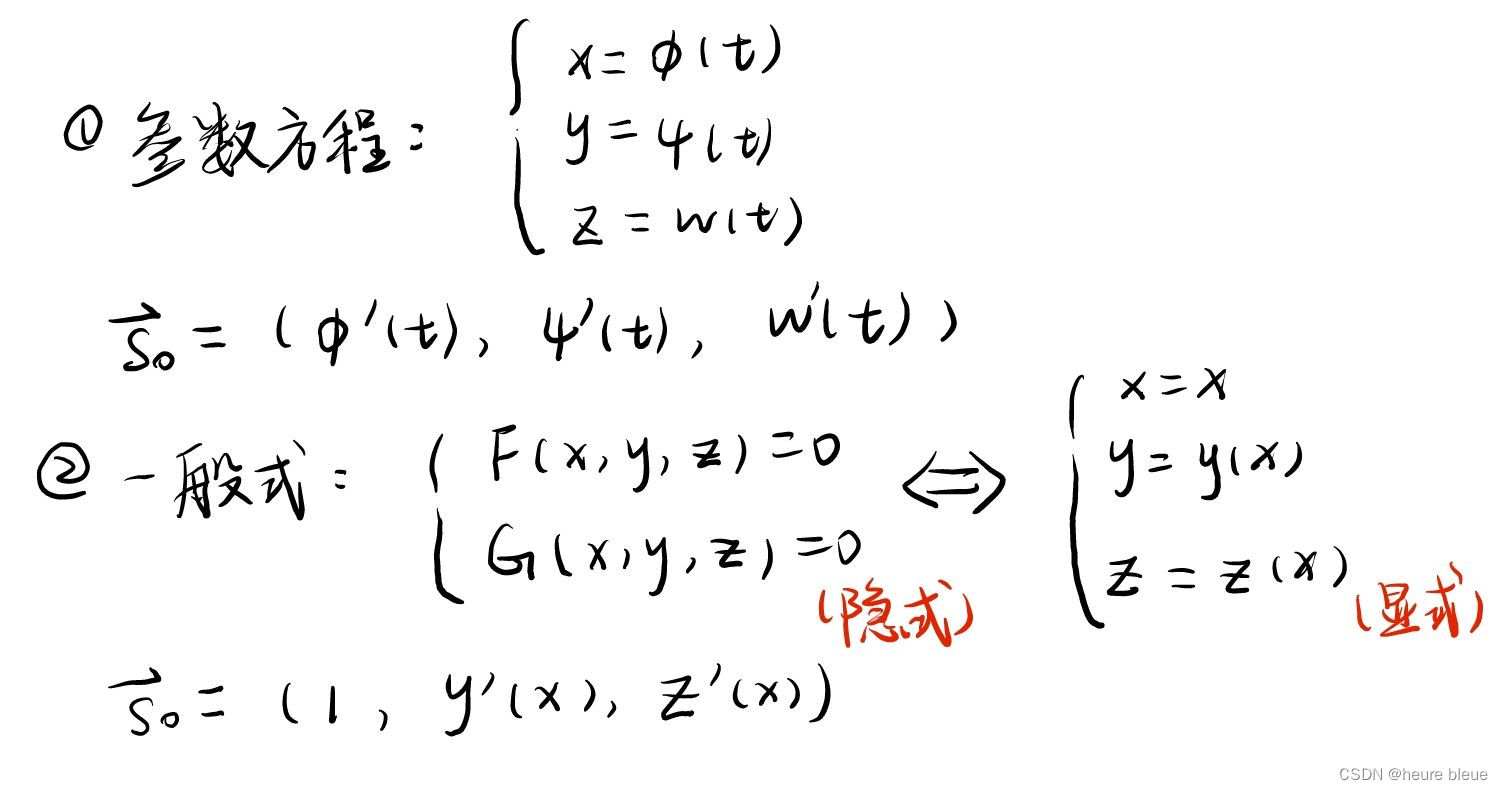
格林公式

证明

相关证明在另一篇格林公式，高斯公式，斯托克斯公式简易理解和串联-CSDN博客

记忆

这里有一个记忆使用格林公式三个限制条件的小tip：闭关锁国

闭：曲线必须是闭曲线

关：关卡是政府机构（正向），为了抵御外敌（外侧）

国：一个国家的历史连续不断（具有一阶连续偏导数）

路径无关

关于路径无关，个人认为它的完整版是“起止点不同，总功只与起止点有关，与路径无关”，且是“起止点相同，总功为0”的孪生结论。

这部分内容我觉得结合物理意义去理解会清楚一点，不然等价命题又多又相似简直要晕死。

其实学过高中物理大家都知道，我们计算功只跟位移有关，与路径无关。而且如果起止位置相同，那就等于没有做功，兜兜转转一大圈回到了起点。

但是，这个认知有一个大前提：做功的力要是保守力。

至于保守力的具体定义在这里就不细究了。总之，力分为保守力和非保守力，而我们高中时期学的结论是建立在保守力场之中才成立的。而我们怎样判断是不是保守力呢，没错——

这个结论是基于格林公式推出的，稍加思考就能理解。

那么我们现在知道，想要做的功为0，需要满足两个条件：

①起止点相同

②做功的力是保守力

记住这两个条件，之后我们所有的题目类型都是基于这两个条件排列组合得出的，在下一小节会进行详细梳理。

现在我们来总结一下基于路径无关的等价命题：

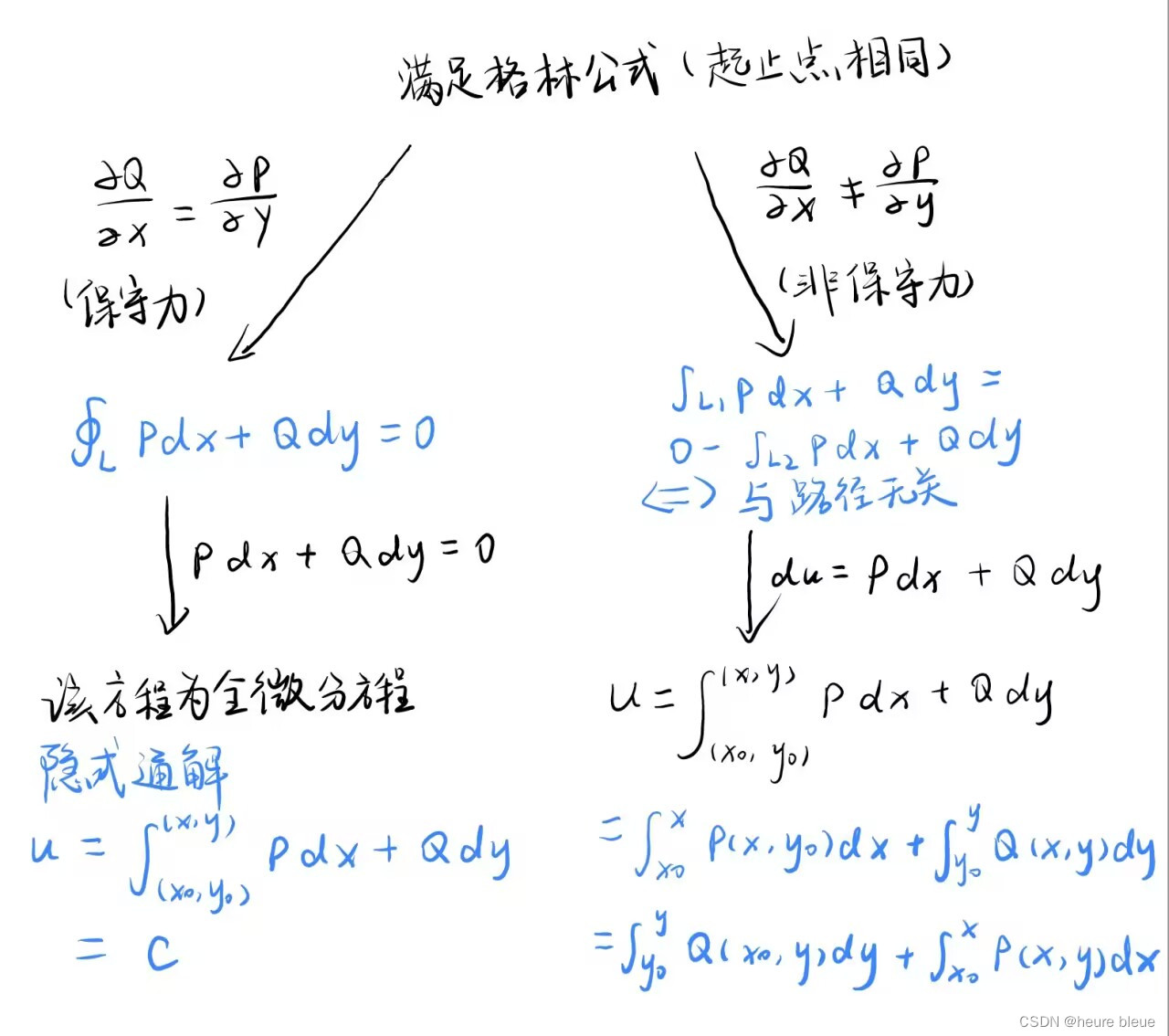
也就是下列命题（一打眼有点晕）：

斯托克斯公式

这是一个没有太多花活儿的公式，只分为能直接用和不能用两种情况（仰天长叹，还是喜欢这种省心的）。

使用条件和格林公式一致。不过它也不能算完全省心，本质上其实是祸水东引，把求第二类曲线积分变成求第二类曲面积分，听起来也没有很简单。

所以它其实就是一个套壳的曲面积分题……这里先不讨论。

通用化简法

在没有公式可用的情况下，我们只能将曲线积分化简为一重积分。由于曲线积分化为一重积分的过程比较简单，只要注意起点和终点位置即可，所以具体原理将在更加复杂的曲面积分化二重积分中一并给出，对比讲解。

除此之外，在第一步投影时，也可以进一步细分为两个办法：分面投影和合并投影。二者没有本质区别。

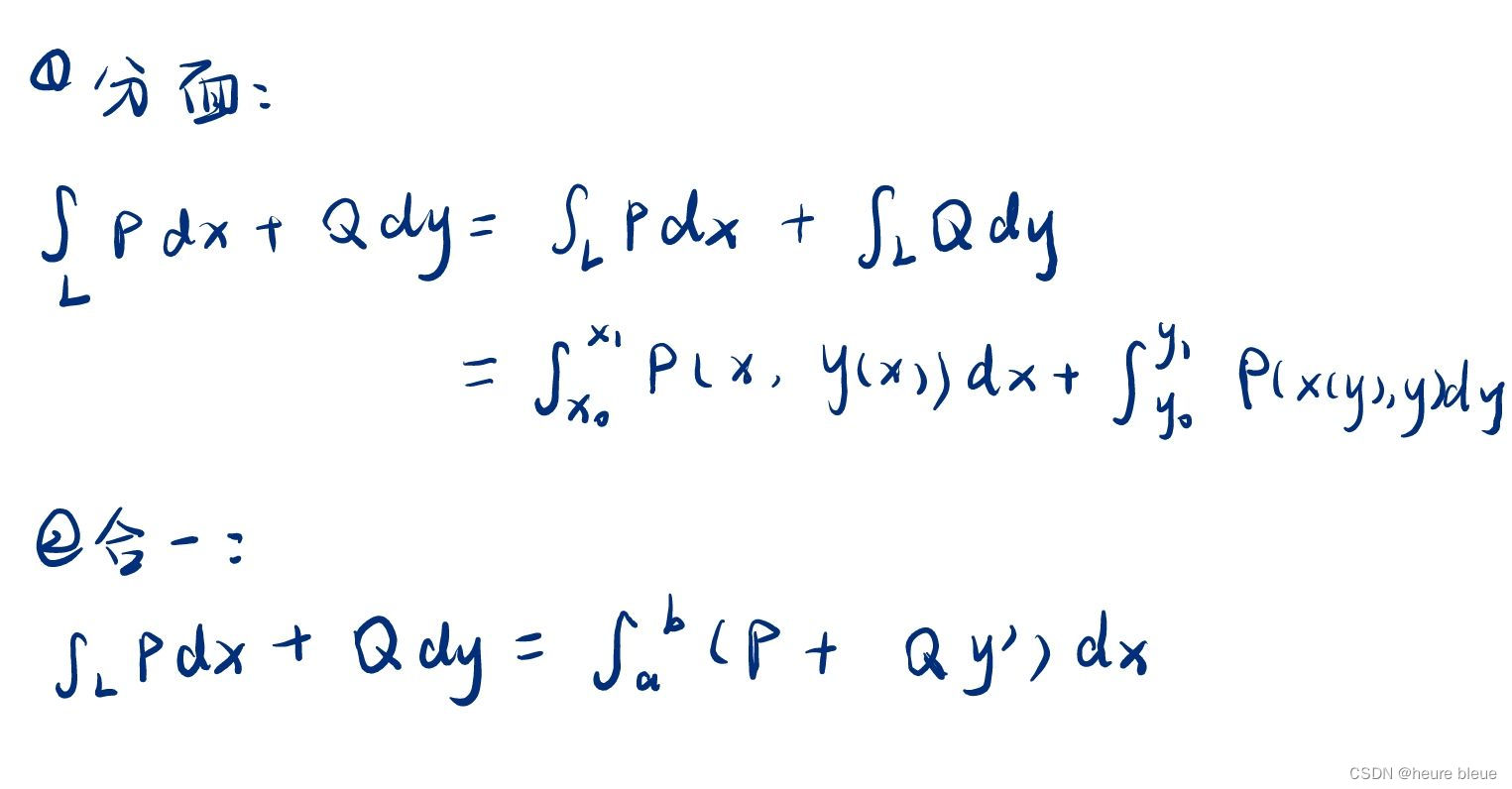
注意这里的分面投影法和上文的等价命题的不同：等价命题是在满足一定条件下可以选择简化路径，被积函数代定值y0；而分面投影没有条件，被积函数不能代定值，而是y(x)。

面向做题的曲线积分小结

为了便于理解，我依然借用物理意义进行总结，把题目按照是否满足“起止点相同”（即是否可用格林公式）和“做功的力是保守力”（即是否满足）这两个条件进行排列组合分类，如下：

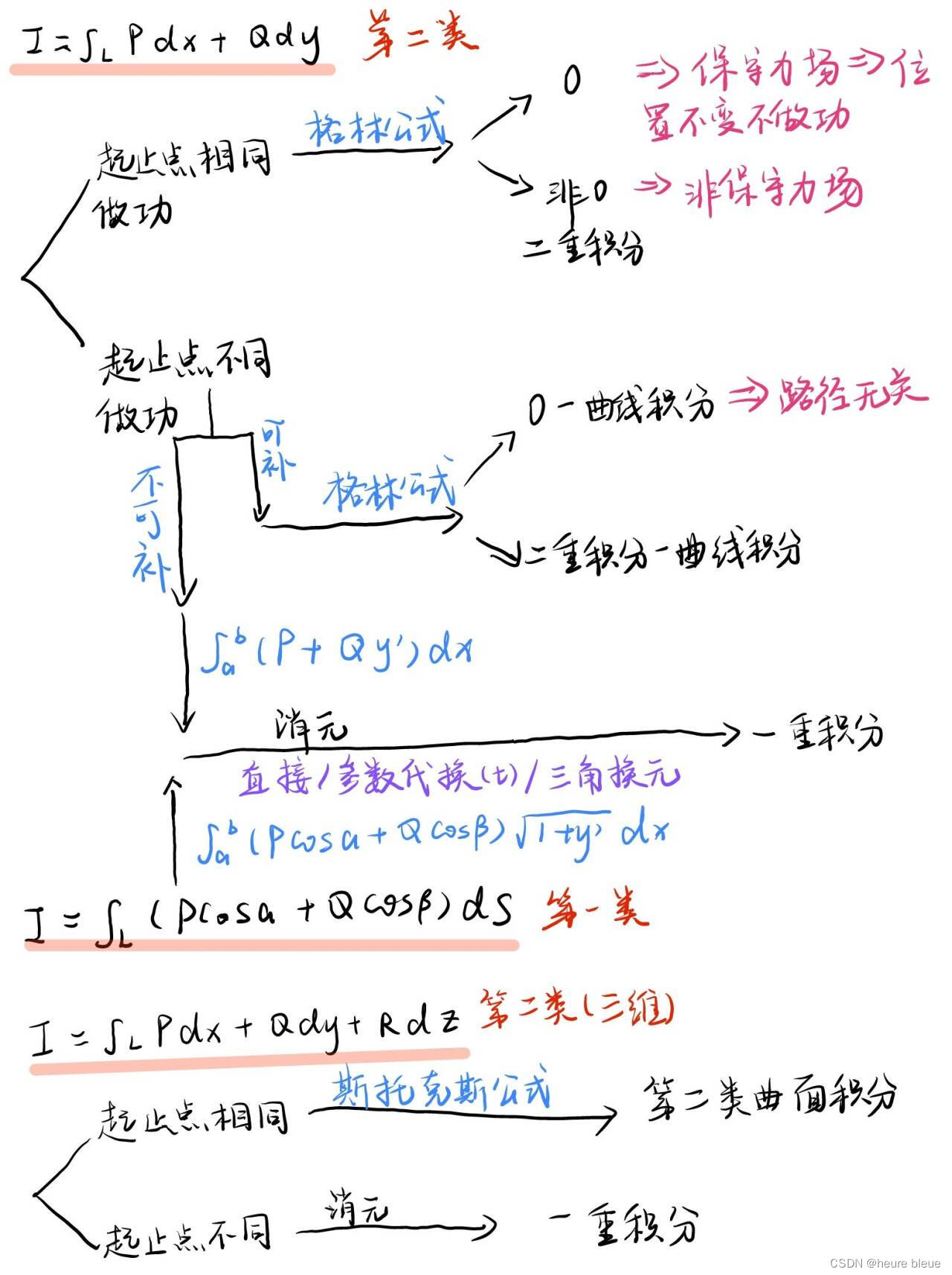
总之，无论是第一类还是第二类曲线积分，我们都是无法直接计算的，所以无论它们之间可以怎样互相转化，最终目标只有一个：化为可计算的一重/二重积分。

其中对于第二类曲线积分，如果满足条件，格林公式可以抄近道直接两下求导化为二重积分；如果不满足条件也要创造条件，加辅助线让它满足条件，这么做虽然没法完全消灭曲线积分，但是能把复杂的路径转为简单的路径；什么，你说实在没法简化，那就老老实实套公式化一重积分吧，过程中留心能不能用对称性作作弊。而对于第一类曲线积分，有且只有一条路，就是化一重积分，核心思想就是消元，把后面部分的变量削到只剩一个，不管是用t参数代换还是三角换元——不然也没法算出来是不。

至于三维情况下的第二类曲线积分，斯托克斯公式正好将它和第二类曲面积分沟通了起来，这部分将在曲面积分小结中进行讲解。