先看一下斐波那契数列
这个很容易理解,就是当前的值等于前两个值的和
斐波那契法的递归结构如下
步骤一:我们首先要知道需要精确到的区间长度,例如要在[1, 10]之间搜索极小值点,希望精确到0.5之间,那么也就是我最后要求得的Ln的长度要小于等于0.5。所以这个时候就能知道经过几轮计算可以达到这个精度,斐波那契数列指的是:Fn=F(n-1)+F(n-2)。上图可知Ln与Fn是有关系的,所以可以求得满足Ln小于等于0.5的Fn,也就知道了可以迭代几轮。
步骤二:求出L2,L2=L1*F(n-1)/F(n),这个式子可以由上图得到,就是要确定最开始的t1、t2点,然后比较t1、t2点对应的函数值得大小,缩小区间,缩小区间的方法跟通用方法一致,如果t1的函数值f1大于t2的函数值f2,那么区间缩小为[t1, 10],否则区间缩小为[1, t2]
步骤三:如果区间缩小为[t1, 10],这个时候t1=t2,而t2的值等于t1在这个区间内的对称值。其实我们可以看到只有第一步需要计算两个点的函数值,其他步都只要计算一个点的函数值就行,因为另外一个点的函数值由上一步遗留下来
代码实现如下
- private static void fibonacci(float start, float end, float eps) {









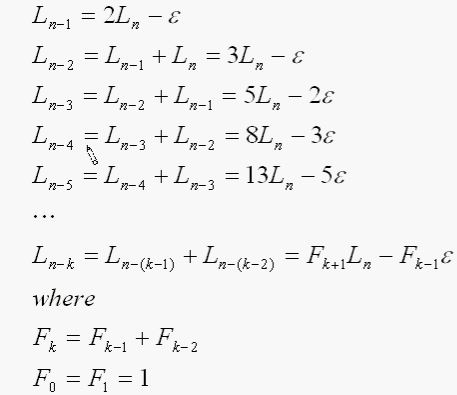
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








