文章目录
CS224W: Machine Learning with Graphs
公式输入请参考: 在线Latex公式
Community Detection in Networks
先看结论:
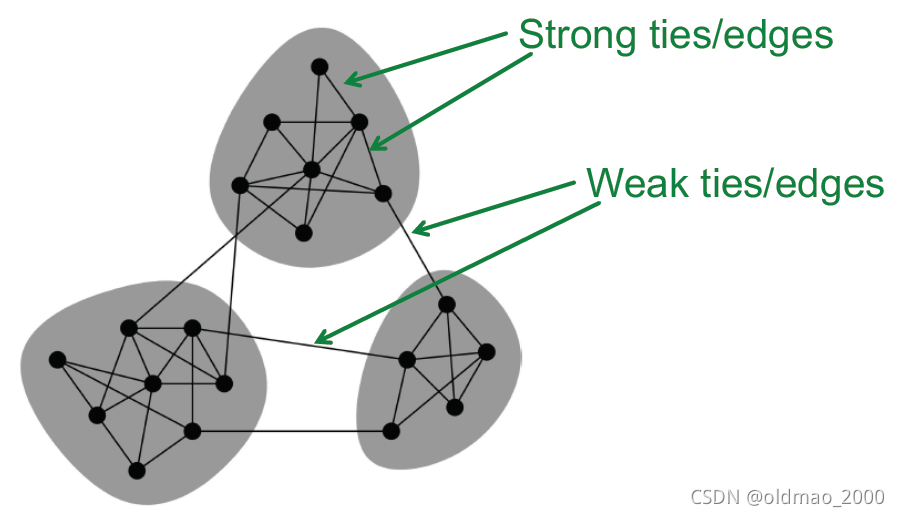
网络中会存在聚集的Community,其内部关系是strong relation,各个Community之间存在weak relation。
Social network视角下的图
在社交网络中,可以把人看做节点,人与人的关系看做边,由于人的关系疏密不一致,可以分成两种,而在边上传递着各种信息流:
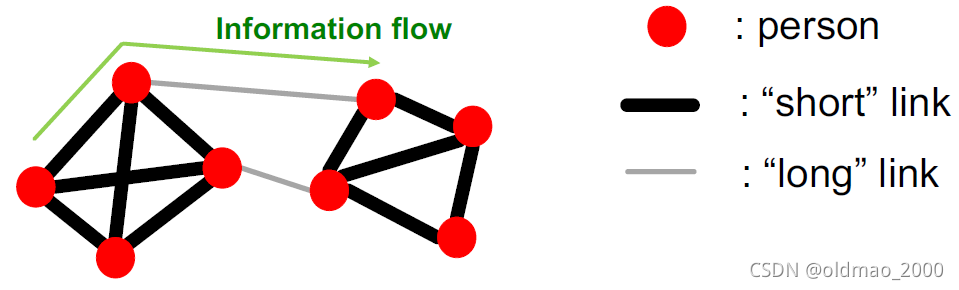
例如,Mark Granovetter在1960年代的博士研究中发现,社交网络中人获取信息的方式不是通过周围的好友,往往是通过一些熟人的方式来获取,例如:同事等。
这个现象出现的原因在于friendships的两个方面:
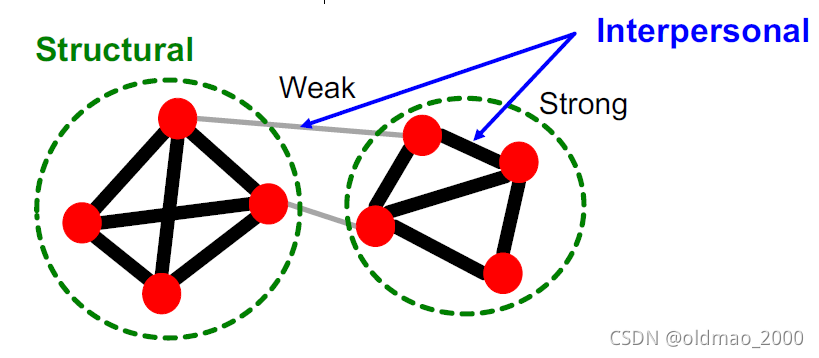
- Structural: Friendships span different parts of the network.
§ Structurally embedded (tightly-connected) edges are also socially strong
§ Long-range edges spanning different parts of the network are socially weak - Interpersonal: Friendship between two people is either strong or weak
当前comunity中的信息往往都是已知的(冗余redundant),从comunity之间的long-range边才能获取更多不同信息,从而帮助当前节点解决问题,例如找工作。
Triadic Closure
Triadic Closure是指在社交网络中,节点往往有三角形的relation关系。
If 𝑩 and 𝑪 have a friend 𝑨 in common, then:
𝑩 is more likely to meet 𝑪
§ (since they both spend time with 𝑨)
𝑩 and 𝑪 trust each other
§ (since they have a friend in common)
𝑨 has incentive to bring 𝑩 and 𝑪 together
§ (since it is hard for 𝑨 to maintain two disjoint relationships)
有研究表明,青少年女生low clustering coefficient,那么suicide倾向较高。
人类就是群居动物。
Edge overlap
下面来看如何量化两个节点间关系的强弱:
O
i
j
=
∣
(
N
(
i
)
∩
N
(
j
)
)
−
{
i
,
j
}
∣
∣
(
N
(
i
)
∪
N
(
j
)
)
−
{
i
,
j
}
∣
O_{ij}=\cfrac{|(N(i)\cap N(j))-\{i,j\}|}{|(N(i)\cup N(j))-\{i,j\}|}
Oij=∣(N(i)∪N(j))−{i,j}∣∣(N(i)∩N(j))−{i,j}∣
N
(
i
)
N(i)
N(i)表示节点i的邻居集合。
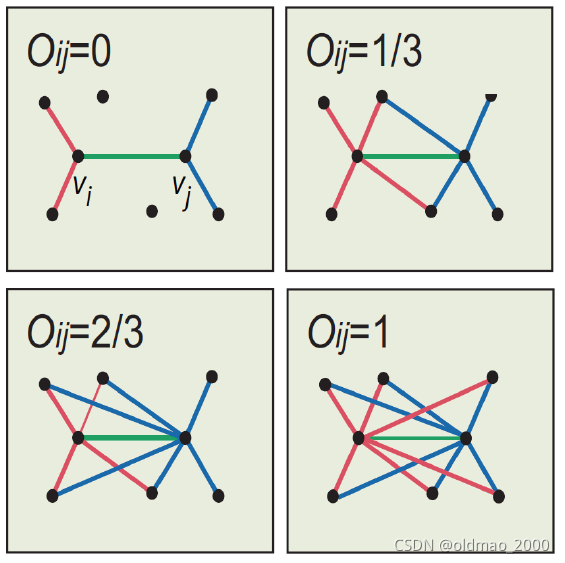
上式中分子是除了ij节点本身外二者的共同邻居,分母是除了ij节点本身外二者所有邻居。
有了这个量化值后,可以看一些实例数据对60年代的理论分析的实证。
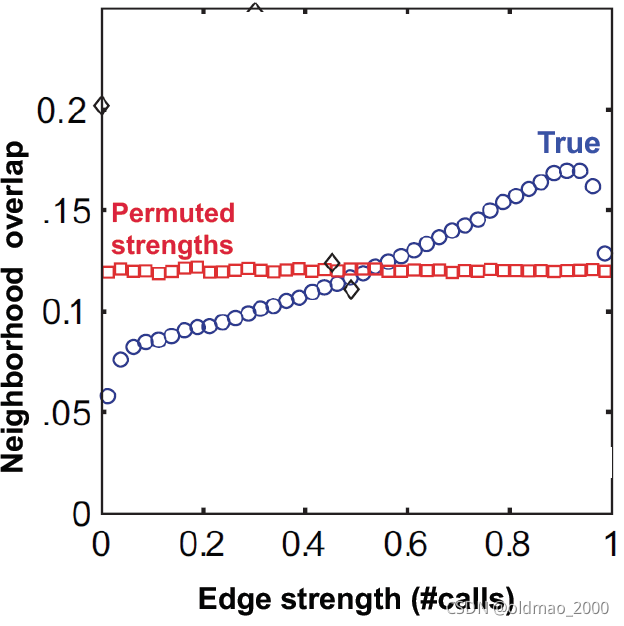
上图中,蓝色是真实的通话数据,红色是保持网络结构不变随机分配通话数量后的结果。
横坐标通话数量和纵坐标edge overlap之间具有正相关性。
将部分数据可视化后(密集community颜色越红):
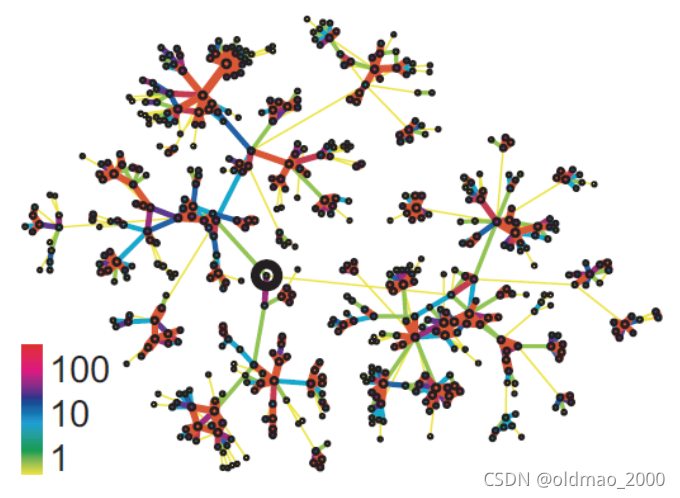
将通信数量随机分配后:
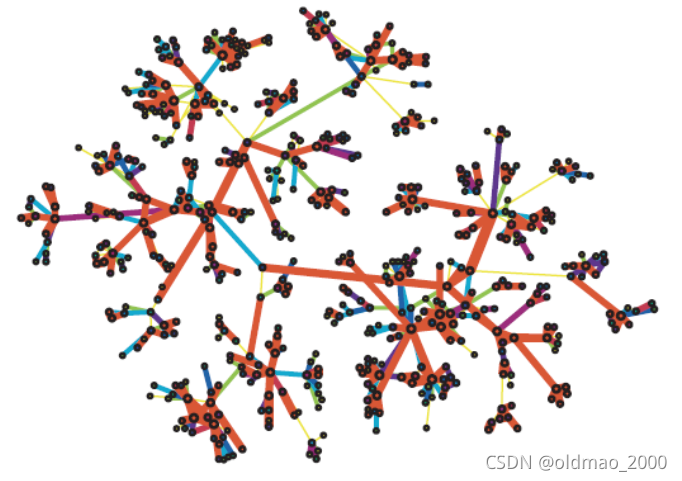
从移边分解实验可以看到
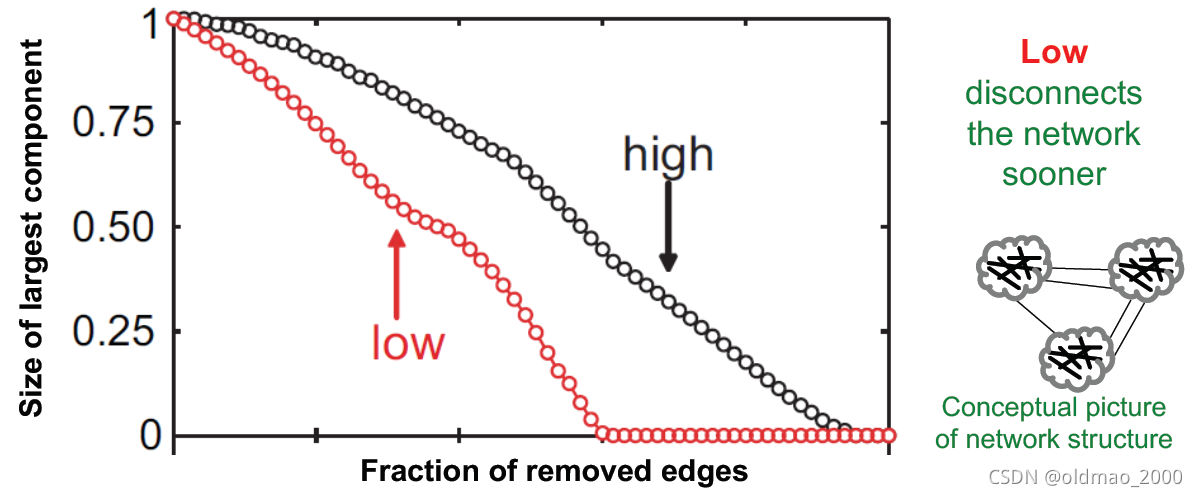
红色是Low to high的overlap移边方式,图分解更快。
黑色是High to low的overlap移边方式,图分解较慢。
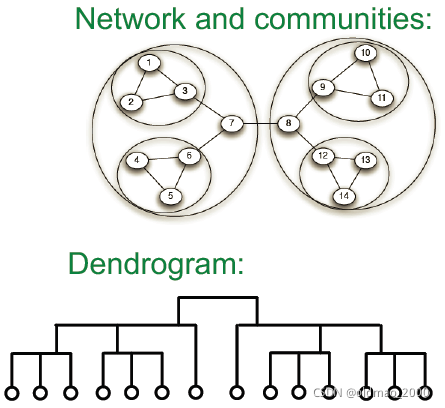
Network Communites
下面在看几个从图中找Network Community的例子,然后看如何在图中用数学的方式把Network Community给定义出来。
Network Community的别名还有:clusters, groups, modules
例子
Zachary’s Karate club network
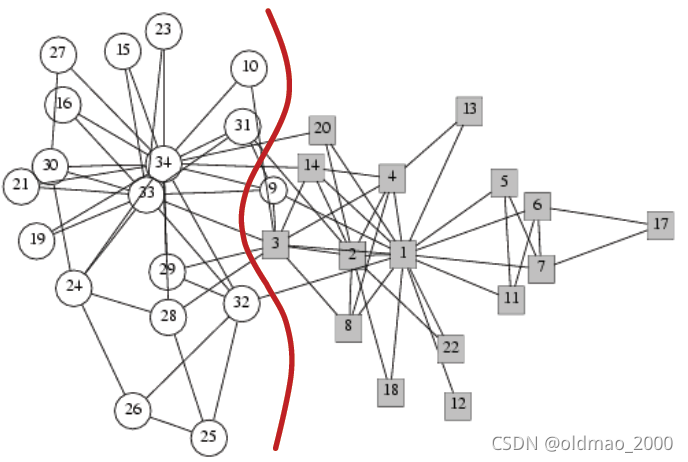
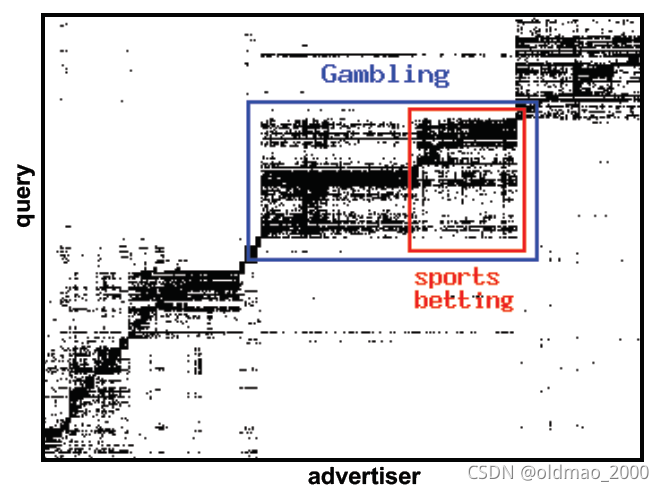
在在线广告投放中,把广告商和查询关键字看做节点,将广告商投放的关键字作为边。可以识别出有针对性的投放区域。
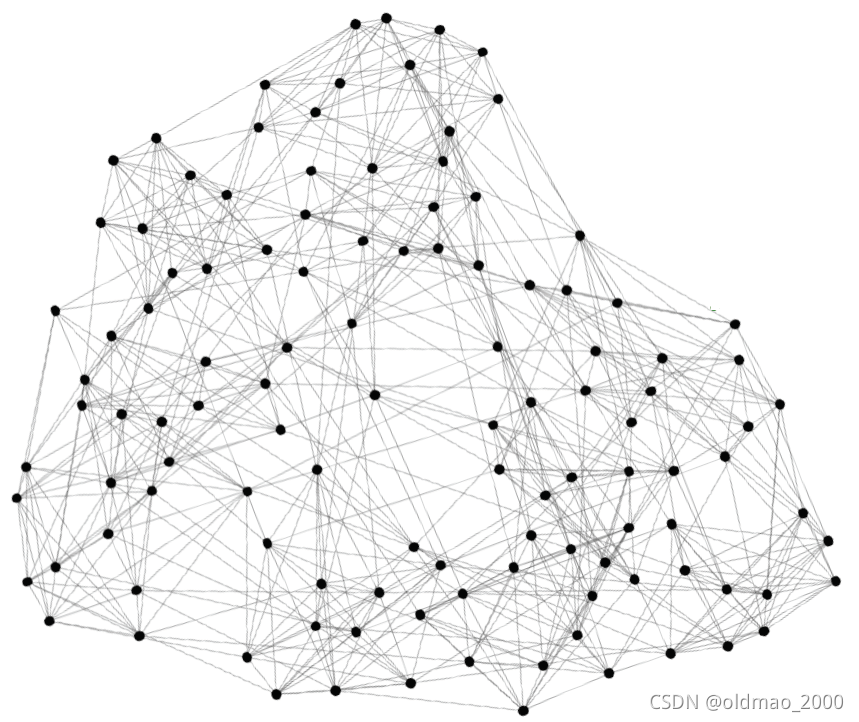
NCAA Football Network,节点是球队,边是球队之间的比赛,原始图这样:
聚类后发现和某些conference(赛区)有关:

下面看如何找community。
Network Communites的模块化程度
Communities: sets of tightly connected nodes
定义: Modularity 𝑸
A measure of how well a network is partitioned into communities.
Given a partitioning of the network into groups disjoint
s
∈
S
s\in S
s∈S:
Q
∝
∑
s
∈
S
[
(
# edges within group
s
)
−
(
expeted # edges within group
s
)
]
Q\propto \sum_{s\in S}[(\text{\# edges within group }s)-(\text{expeted \# edges within group }s)]
Q∝s∈S∑[(# edges within group s)−(expeted # edges within group s)]
这里的后面一项比较难理解,是一个期望,实际上是需要使用随机图(Null Model)来求。
Null Model
给定一个实际的图
G
G
G,该图包含
n
n
n个节点,
m
m
m条边,根据图
G
G
G保持节点和边数量不变(Same degree distribution but uniformly random connections),重新分配边的连接得到图
G
′
G'
G′,而且图
G
′
G'
G′是multigraph,就是允许两个节点间有多条边。
接下来算期望。
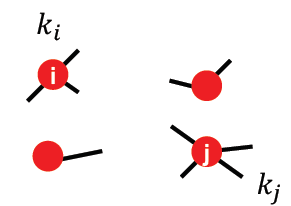
如果把边看成双向的,那么共有
2
m
2m
2m条有向边(这样算是因为节点都象上图一样切开了,每个点的条幅数量加起来就是
2
m
2m
2m),对于出度为
k
i
k_i
ki的
i
i
i节点,其重新连接到节点
j
j
j的概率是:
k
j
2
m
\cfrac{k_j}{2m}
2mkj,因此重连
i
,
j
i,j
i,j的边的数量期望是:
k
i
⋅
k
j
2
m
=
k
i
k
j
2
m
k_i\cdot \cfrac{k_j}{2m}=\cfrac{k_ik_j}{2m}
ki⋅2mkj=2mkikj
那么计算
G
′
G'
G′的期望总边数为:
G
e
d
g
e
s
_
n
u
m
′
=
1
2
∑
i
∈
N
∑
j
∈
N
k
i
k
j
2
m
=
1
2
⋅
1
2
m
∑
i
∈
N
k
i
(
∑
j
∈
N
k
j
)
=
1
4
m
2
m
⋅
2
m
=
m
G'_{edges\_num}=\cfrac{1}{2}\sum_{i\in N}\sum_{j\in N}\cfrac{k_ik_j}{2m}=\cfrac{1}{2}\cdot\cfrac{1}{2m}\sum_{i\in N}k_i\left(\sum_{j\in N}k_j\right)=\cfrac{1}{4m}2m\cdot2m=m
Gedges_num′=21i∈N∑j∈N∑2mkikj=21⋅2m1i∈N∑ki⎝⎛j∈N∑kj⎠⎞=4m12m⋅2m=m
这里因为条件中讲了,所有节点的边(度)加起来是
2
m
2m
2m,因此:
∑
i
∈
N
k
i
=
∑
i
∈
N
k
j
=
2
m
\sum_{i\in N}k_i=\sum_{i\in N}k_j=2m
i∈N∑ki=i∈N∑kj=2m
这里也证明了Null Model中与原图的度是一致的。
注意:Null Model可以用在有权图中,有权图可以把权重与度做乘积即可。
Modularity
具体来算Modularity,根据上面的公式:
Q
∝
∑
s
∈
S
[
(
# edges within group
s
)
−
(
expeted # edges within group
s
)
]
Q\propto \sum_{s\in S}[(\text{\# edges within group }s)-(\text{expeted \# edges within group }s)]
Q∝s∈S∑[(# edges within group s)−(expeted # edges within group s)]
加上具体的数学表达,Modularity公式变成:
Q
(
G
,
S
)
=
1
2
m
∑
s
∈
S
∑
i
∈
S
∑
j
∈
S
(
A
i
j
−
k
i
k
j
2
m
)
Q(G,S)=\cfrac{1}{2m}\sum_{s\in S}\sum_{i\in S}\sum_{j\in S}\left(A_{ij}-\cfrac{k_ik_j}{2m}\right)
Q(G,S)=2m1s∈S∑i∈S∑j∈S∑(Aij−2mkikj)
这里的
1
2
m
\cfrac{1}{2m}
2m1相当于归一化常数,使得
−
1
≤
Q
≤
1
-1\le Q\le 1
−1≤Q≤1
A就是邻接矩阵(可以是有权图)。
如果
S
S
S中的边比随机图中边(期望数量)要多,上面括号里面的值就为正,说明
S
S
S中边要比随机图要密集。一般
Q
Q
Q在0.3-0.7之间就意味图中有非常明显的community结构。
Modularity的最终形式如下:
Q
(
G
,
S
)
=
1
2
m
∑
i
j
[
A
i
j
−
k
i
k
j
2
m
]
δ
(
c
i
,
c
j
)
(1)
Q(G,S)=\cfrac{1}{2m}\sum_{ij}\left[A_{ij}-\cfrac{k_ik_j}{2m}\right]\delta(c_i,c_j)\tag1
Q(G,S)=2m1ij∑[Aij−2mkikj]δ(ci,cj)(1)
这里的
c
i
,
c
j
c_i,cj
ci,cj是同一社区的节点
δ
\delta
δ是indicator函数,当两个节点来自相同社区
δ
(
c
i
,
c
j
)
=
1
\delta(c_i,c_j)=1
δ(ci,cj)=1否则为0
我们可以通过最大化modularity来找出community。
Louvain Algorithm
下面用Louvain算法来最大化modularity来找出community
算法概述
Louvain Algorithm是一个贪心算法,时间复杂度为:
O
(
n
log
n
)
O(n\log n)
O(nlogn)
该算法支持有权图(无权图可以看做边的权重都为1),最后的结果是层次结构的。
算法可用于大型网络,原因是:
算法快
收敛快
可得到高modularity的输出
整个算法可以分两个步骤:
步骤1:(重点):Modularity is optimized by allowing only local changes to node-communities memberships.
步骤2:The identified communities are aggregated into super-nodes to build a new network
跳转步骤1,直到网络收敛(The passes are repeated iteratively untilno increase of modularity is possible)
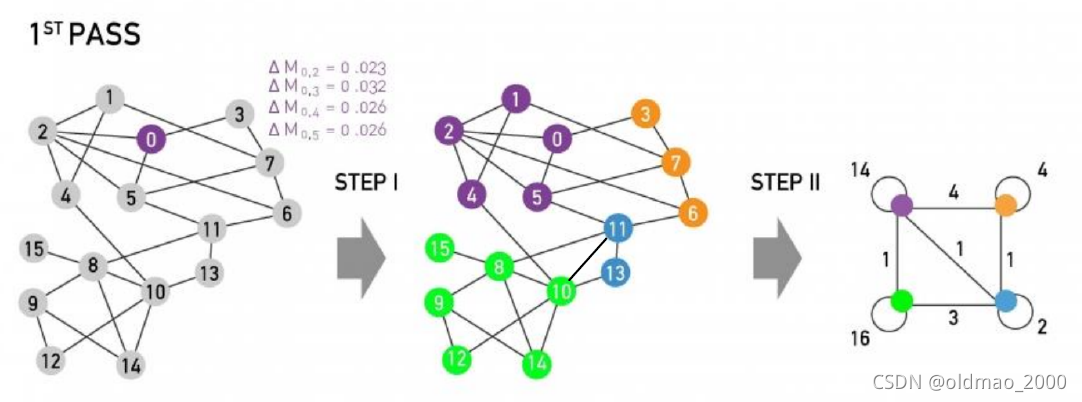
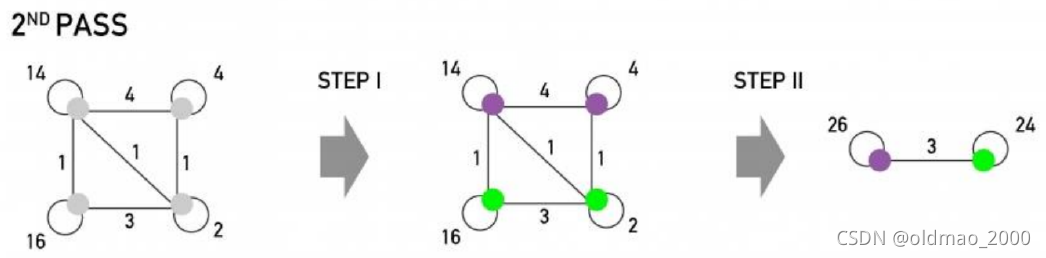
步骤1
先给出大概的描述,再看具体算法。
1.先将图中每一个单独的节点看做一个community。
2.对每个一个节点
i
i
i,执行两个计算
2.1计算将节点
i
i
i加入节点
i
i
i的邻居节点
j
j
j所在社区后的modularity值:
Δ
Q
\Delta Q
ΔQ
2.2确定将节点
i
i
i加入邻居节点
j
j
j所在社区,使得
Δ
Q
\Delta Q
ΔQ最大
3.当modularity值不再增加时,步骤1结束
选择不同的节点
i
i
i计算得到modularity值会有所不一样,但是研究表明,这基本不会影响最终的community划分
计算 Δ Q \Delta Q ΔQ
我们假设节点
i
i
i当前所在社区为
D
D
D,移动到其邻接节点
j
j
j所在社区为
C
C
C,那么:
Δ
Q
(
D
→
i
→
C
)
=
Δ
Q
(
D
→
i
)
+
Δ
Q
(
i
→
C
)
\Delta Q(D\rightarrow i\rightarrow C)=\Delta Q(D\rightarrow i)+\Delta Q( i\rightarrow C)
ΔQ(D→i→C)=ΔQ(D→i)+ΔQ(i→C)
对应的图例为:
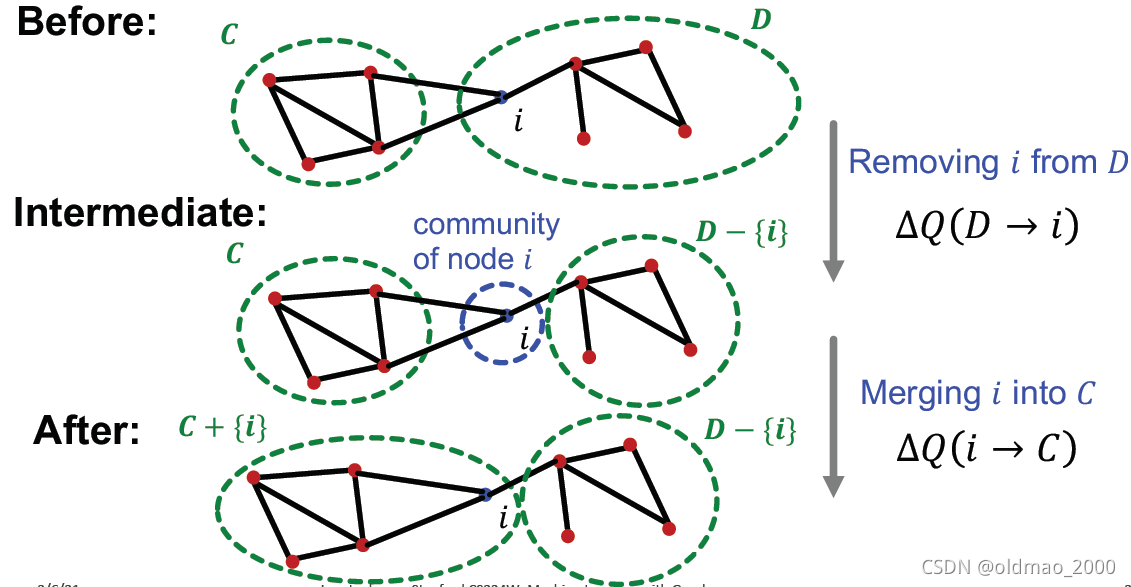
下面来推导等式右边的两项,先看
Δ
Q
(
i
→
C
)
\Delta Q( i\rightarrow C)
ΔQ(i→C)
推导 Δ Q ( C ) \Delta Q(C) ΔQ(C)
先算社区
C
C
C的modularity:
Q
(
C
)
Q(C)
Q(C)
设:
∑
i
n
≡
∑
i
,
j
∈
C
A
i
j
(2)
\sum_{in}\equiv \sum_{i,j\in C}A_{ij}\tag2
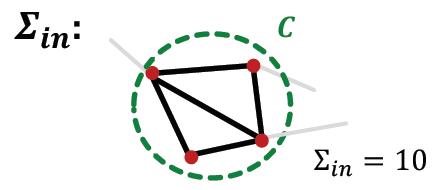
in∑≡i,j∈C∑Aij(2)
记为社区
C
C
C中节点内部边的权重和,
A
A
A是邻接矩阵,
i
,
j
i,j
i,j是
C
C
C中任意两个节点。
∑
t
o
t
≡
∑
i
∈
C
k
i
(3)
\sum_{tot}\equiv \sum_{i\in C}k_{i}\tag3
tot∑≡i∈C∑ki(3)
记为社区
C
C
C中节点所有边的权重和,tot是total的缩写。
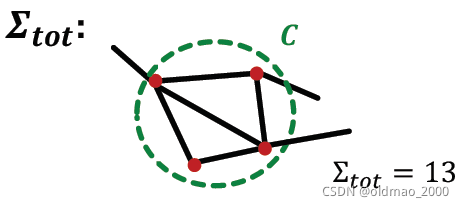
从图例中可以看到为了兼容有向图,这里的无向图边算了2次,看不懂会前面看modularity推导。根据公式1,我们可以得到:
Q
(
C
)
≡
1
2
m
∑
i
,
j
∈
C
[
A
i
j
−
k
i
k
j
2
m
]
δ
(
c
i
,
c
j
)
Q(C)\equiv\cfrac{1}{2m}\sum_{i,j\in C}\left[A_{ij}-\cfrac{k_ik_j}{2m}\right]\delta(c_i,c_j)
Q(C)≡2m1i,j∈C∑[Aij−2mkikj]δ(ci,cj)
这里由于
i
,
j
i,j
i,j都来自相同社区
C
C
C,因此indicator function
δ
\delta
δ值为1,然后把前面的
1
2
m
\cfrac{1}{2m}
2m1放进去:
Q
(
C
)
=
∑
i
,
j
∈
C
A
i
j
2
m
−
(
∑
i
∈
C
k
i
)
(
∑
j
∈
C
k
j
)
(
2
m
)
2
Q(C)=\cfrac{\sum_{i,j\in C}A_{ij}}{2m}-\cfrac{(\sum_{i\in C}k_i)(\sum_{j\in C}k_j)}{(2m)^2}
Q(C)=2m∑i,j∈CAij−(2m)2(∑i∈Cki)(∑j∈Ckj)
将公式2和3带入:
Q
(
C
)
=
∑
i
n
2
m
−
(
∑
t
o
t
2
m
)
2
Q(C)=\cfrac{\sum_{in}}{2m}-\left(\cfrac{\sum_{tot}}{2m}\right)^2
Q(C)=2m∑in−(2m∑tot)2
上式中第一项是社区节点内部的边权重,后面一项是社区节点所有边的权重
当社区内部节点的边权重越大,
Q
(
C
)
Q(C)
Q(C)就越大。
推导 Δ Q ( i → C ) \Delta Q( i\rightarrow C) ΔQ(i→C)
进一步定义:
k
i
,
i
n
≡
∑
j
∈
C
A
i
j
+
∑
j
∈
C
A
j
i
(4)
k_{i,in}\equiv \sum_{j\in C}A_{ij}+\sum_{j\in C}A_{ji}\tag4
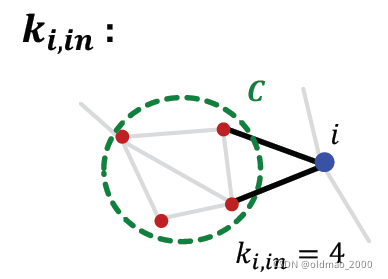
ki,in≡j∈C∑Aij+j∈C∑Aji(4)
节点
i
i
i在社区
C
C
C外面,它与社区内部的权重和记为
k
i
,
i
n
k_{i,in}
ki,in,同样算两次
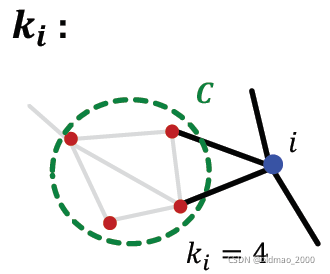
同样记节点
i
i
i的权重和(其实就是度)为
k
i
k_i
ki
那么在节点
i
i
i加入社区
C
C
C之前,计算公式为:
Q
b
e
f
o
r
e
=
Q
(
C
)
+
Q
(
{
i
}
)
=
[
∑
i
n
2
m
−
(
∑
t
o
t
2
m
)
2
]
+
[
0
−
(
k
i
2
m
)
2
]
=
[
∑
i
n
2
m
−
(
∑
t
o
t
2
m
)
2
−
(
k
i
2
m
)
2
]
(5)
\begin{aligned}Q_{before}&=Q(C)+Q(\{i\})\\ &=\left[\cfrac{\sum_{in}}{2m}-\left(\cfrac{\sum_{tot}}{2m}\right)^2\right]+\left[0-\left(\cfrac{k_i}{2m}\right)^2\right]\\ &=\left[\cfrac{\sum_{in}}{2m}-\left(\cfrac{\sum_{tot}}{2m}\right)^2-\left(\cfrac{k_i}{2m}\right)^2\right]\end{aligned}\tag5
Qbefore=Q(C)+Q({i})=⎣⎡2m∑in−(2m∑tot)2⎦⎤+⎣⎡0−(2mki)2⎦⎤=⎣⎡2m∑in−(2m∑tot)2−(2mki)2⎦⎤(5)
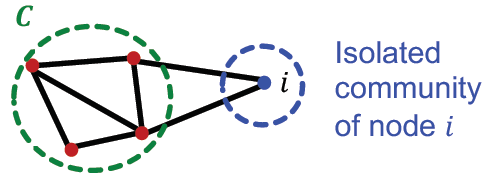
在节点
i
i
i加入社区
C
C
C之后,计算公式为:
Q
a
f
t
e
r
=
Q
(
C
+
{
i
}
)
=
∑
i
n
+
k
i
,
i
n
2
m
−
(
∑
t
o
t
+
k
i
2
m
)
2
(6)
\begin{aligned}Q_{after}&=Q(C+\{i\})\\ &=\cfrac{\sum_{in}+k_{i,in}}{2m}-\left(\cfrac{\sum_{tot}+k_i}{2m}\right)^2\end{aligned}\tag6
Qafter=Q(C+{i})=2m∑in+ki,in−(2m∑tot+ki)2(6)
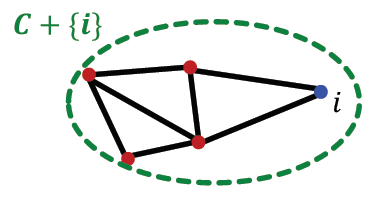
第一项的分子
∑
i
n
+
k
i
,
i
n
\sum_{in}+k_{i,in}
∑in+ki,in相当于计算新社区
C
+
{
i
}
C+\{i\}
C+{i}的内部边权重:
∑
i
n
a
f
t
e
r
\sum_{in_{after}}
∑inafter
第二项的分子
∑
t
o
t
+
k
i
\sum_{tot}+k_i
∑tot+ki相当于计算新社区
C
+
{
i
}
C+\{i\}
C+{i}的所有边权重:
∑
t
o
t
a
f
t
e
r
\sum_{tot_{after}}
∑totafter
感觉第二项多加几条边。。。
根据公式5和6:
Δ
Q
(
i
→
C
)
=
Q
a
f
t
e
r
−
Q
b
e
f
o
r
e
=
∑
i
n
+
k
i
,
i
n
2
m
−
(
∑
t
o
t
+
k
i
2
m
)
2
−
[
∑
i
n
2
m
−
(
∑
t
o
t
2
m
)
2
−
(
k
i
2
m
)
2
]
\begin{aligned}\Delta Q( i\rightarrow C)&=Q_{after}-Q_{before}\\ &=\cfrac{\sum_{in}+k_{i,in}}{2m}-\left(\cfrac{\sum_{tot}+k_i}{2m}\right)^2-\left[\cfrac{\sum_{in}}{2m}-\left(\cfrac{\sum_{tot}}{2m}\right)^2-\left(\cfrac{k_i}{2m}\right)^2\right]\end{aligned}
ΔQ(i→C)=Qafter−Qbefore=2m∑in+ki,in−(2m∑tot+ki)2−⎣⎡2m∑in−(2m∑tot)2−(2mki)2⎦⎤
有了这个结论,
Δ
Q
(
D
→
i
)
\Delta Q(D\rightarrow i)
ΔQ(D→i)也可以计算,因此:
Δ
Q
(
D
→
i
→
C
)
=
Δ
Q
(
D
→
i
)
+
Δ
Q
(
i
→
C
)
\Delta Q(D\rightarrow i\rightarrow C)=\Delta Q(D\rightarrow i)+\Delta Q( i\rightarrow C)
ΔQ(D→i→C)=ΔQ(D→i)+ΔQ(i→C)
也相应的可以算出来。
步骤1的迭代及其终止
重复步骤1直到没有节点移动到新的社区:
对社区
C
C
C中每个节点
i
i
i,计算其最佳社区
C
′
C'
C′,使其满足:
C
′
=
arg max
c
′
Δ
C
(
D
→
i
→
C
′
)
C'=\argmax_{c'}\Delta C(D\rightarrow i\rightarrow C')
C′=c′argmaxΔC(D→i→C′)
如果计算得到的
Δ
C
(
D
→
i
→
C
′
)
>
0
\Delta C(D\rightarrow i\rightarrow C')>0
ΔC(D→i→C′)>0,则将节点
i
i
i从原社区C中移动到
C
′
C'
C′中
PS:这里的Notation前后有点不搭,C在前面是目标社区。
步骤2
这个步骤相对简单一些。
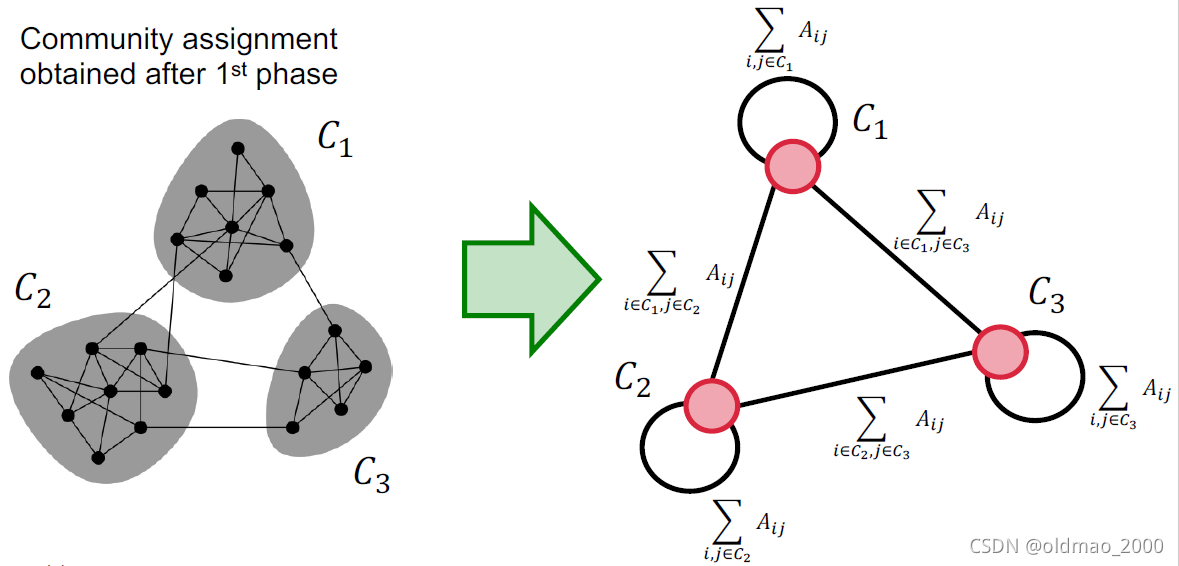
将上一步得到结果中的各个社区看做一个个super-nodes,然后得到新的一个网络,并将步骤1中的计算过程在新网络中再玩一次。
对于新网络创建,需要注意下面两点:
1.如果上一步的两个社区之间有若干个边相连,那么两个社区对应的super-nodes也相连;
2.两个super-nodes相连的边的权重等于两个社区之间所有相连边的权重和。
实例
比利时人的通话网络可视化结果
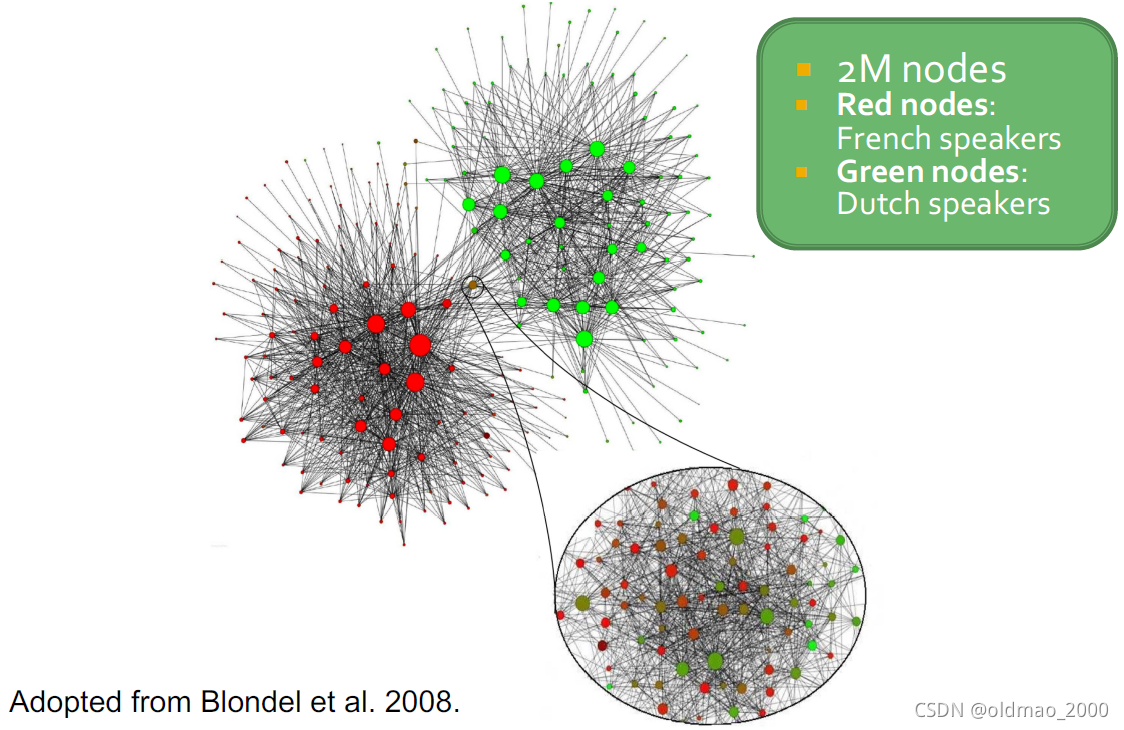
说法语的人通常和相同语言人通话,造成了整个网络分化成两个大的阵营。
Detecting Overlapping Communities: BigCLAM
虽然区分图中的聚类可以得到不同的community,但是实际生活中各个community之间可能会有重叠:
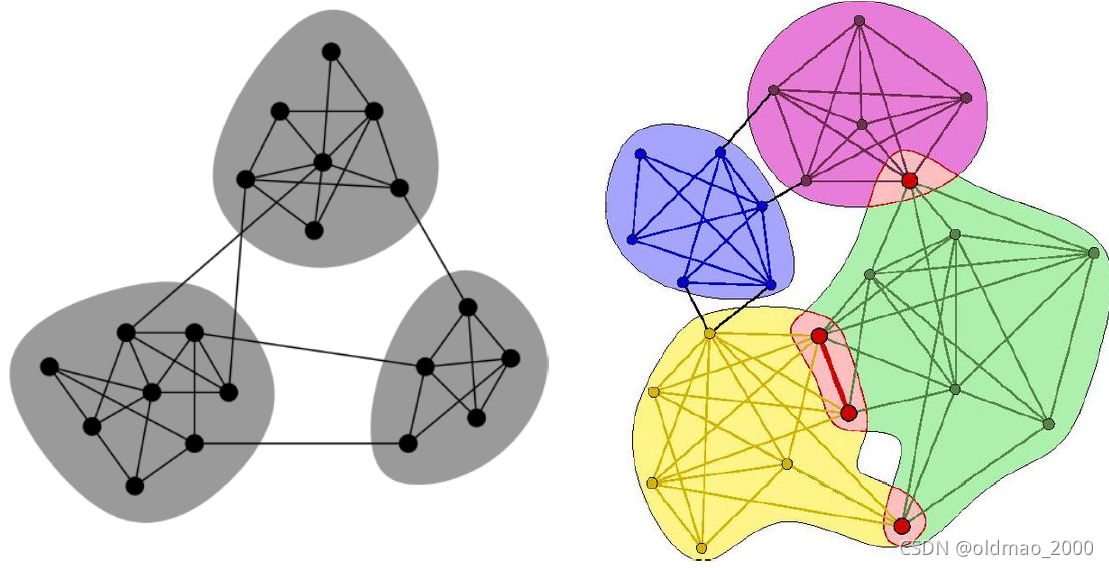
对于左边的Non-overlapping Network
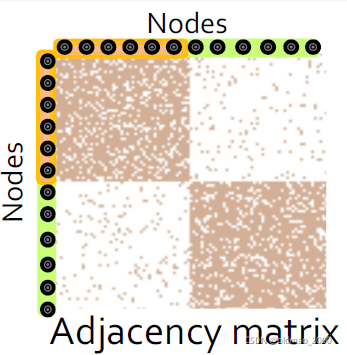
对于右边的Overlapping Network

例如在非死不可的Ego网络中:
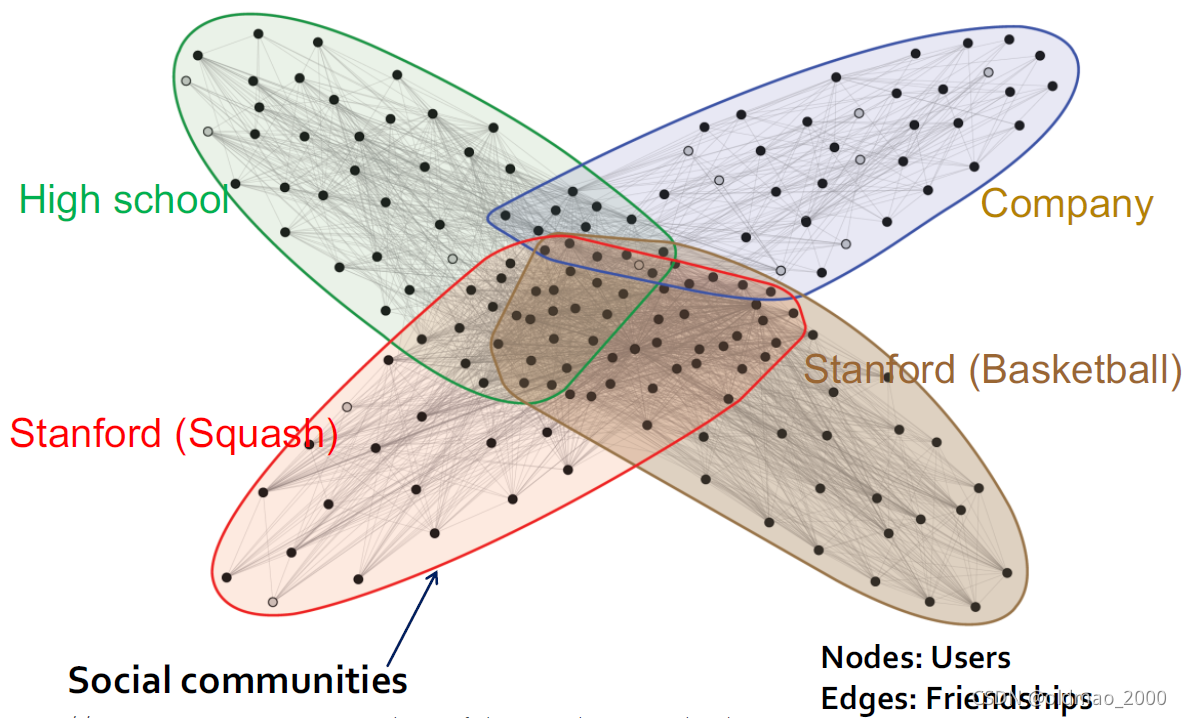
有些节点会属于多个社区,图中有空心节点表示分类错误的结果。
对于蛋白质网络,可以看到类似结果:
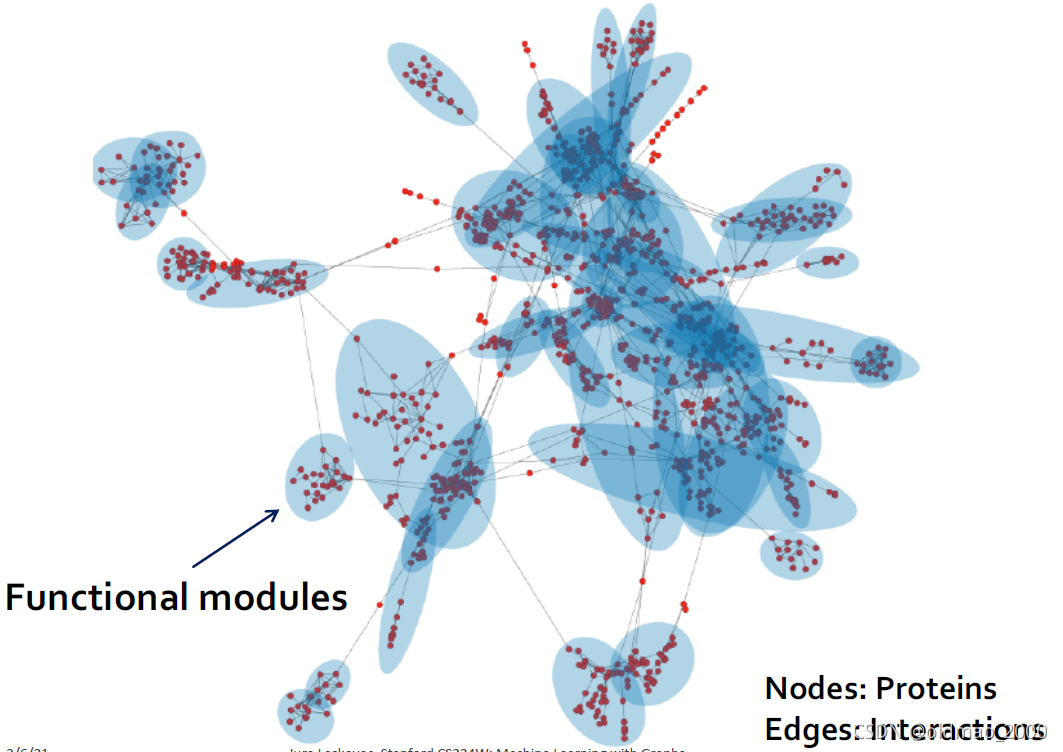
下面就要讲如何找出图中的重叠的部分。大概两步:
步骤1:定义一个基于节点社区图生成模型:Community Affiliation Graph Model (AGM)
步骤2:假设图
G
G
G由AGM算法生成,找出最有可能生成图
G
G
G的AGM模型,并通过该模型来找出重叠社区。
AGM
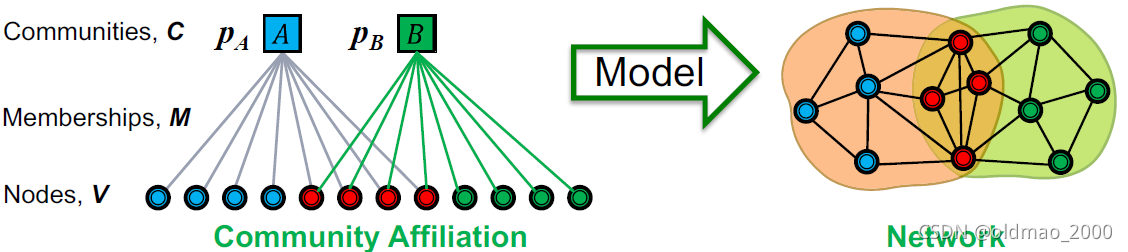
上图是AGM模型生成图的过程,可以看到,模型有几个参数:
Nodes
V
V
V
Communities
C
C
C
Memberships
M
M
M
以及每个Community
C
C
C中各个节点有
p
c
p_c
pc的概率相连
可以理解为有一个硬币,它丢出去朝上的概率是
p
c
p_c
pc,然后让Community
C
C
C中每个节点和其他节点之间用丢硬币的方式来决定,是否有边相连。
如果一个节点属于多个Communities,那么该节点会拥有多次丢硬币的机会,因此,属于多个社区的两个节点有更大几率建立连接。
图中任意两个节点有边的概率可以写成:
p
(
u
,
v
)
=
1
−
∏
c
∈
M
u
∩
M
v
(
1
−
p
c
)
p(u,v)=1-\prod_{c\in M_u\cap M_v}(1-p_c)
p(u,v)=1−c∈Mu∩Mv∏(1−pc)
p
c
p_c
pc是两个节点有边的概率,
1
−
p
c
1-p_c
1−pc是两个节点没有边的概率,
c
∈
M
u
∩
M
v
c\in M_u\cap M_v
c∈Mu∩Mv表示两个节点属于相同社区,
∏
c
∈
M
u
∩
M
v
\prod_{c\in M_u\cap M_v}
∏c∈Mu∩Mv表示两个节点属于相同社区有多个,这么多个社区在丢硬币的时候都没有创建出边,1减去没有创建出边的概率就得到创建边的概率了。
视频中的机器翻译容易误导,这里还是听原音比较好理解。
可以这样想,我有三个骰子,求下丢出不是三颗都是一点的几率?
1
−
三
颗
都
是
一
点
的
概
率
=
1
−
1
6
×
1
6
×
1
6
1-三颗都是一点的概率=1-\cfrac{1}{6}\times \cfrac{1}{6}\times \cfrac{1}{6}
1−三颗都是一点的概率=1−61×61×61
注意:实作上会为所有节点添加全局社区
e
p
s
i
l
o
n
epsilon
epsilon,使得所有节点都有一定概率相连。
创建出来的图有几种结果:
1.Dense Overlaps
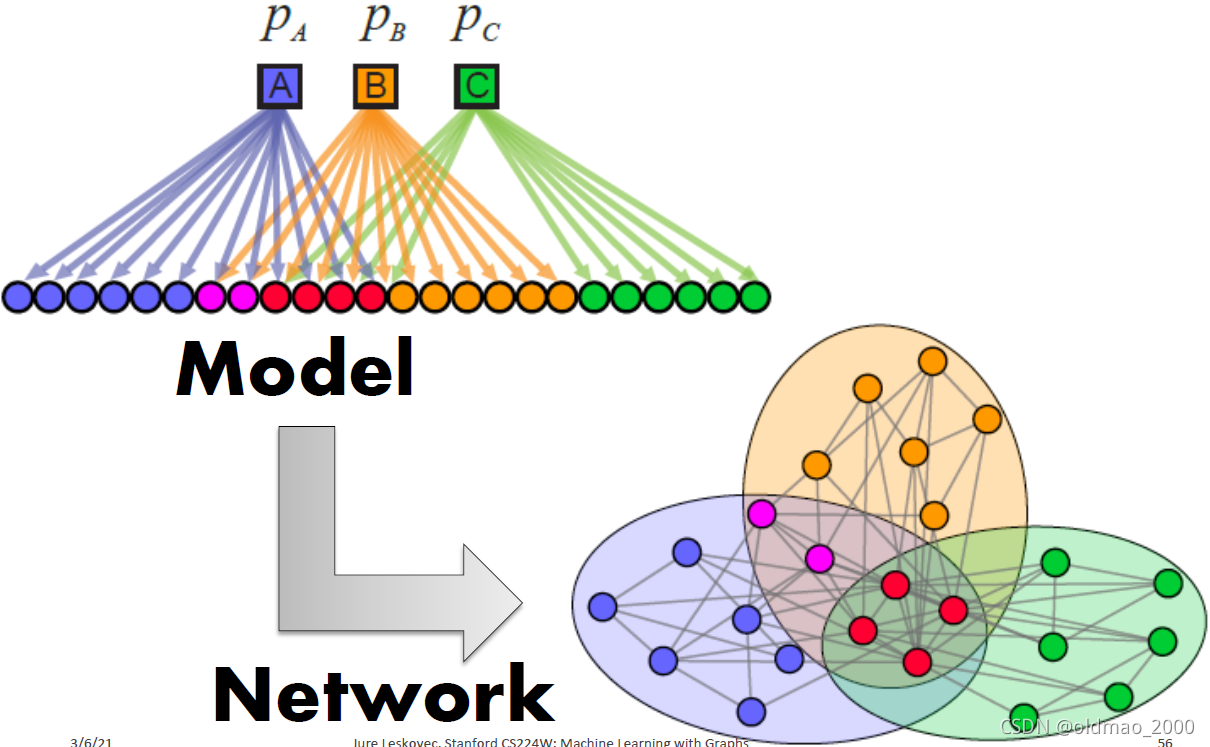
2.Non-overlapping
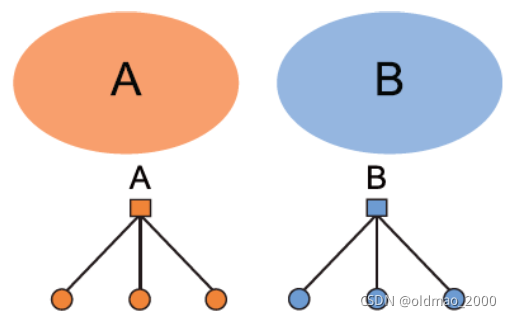
3.Overlapping
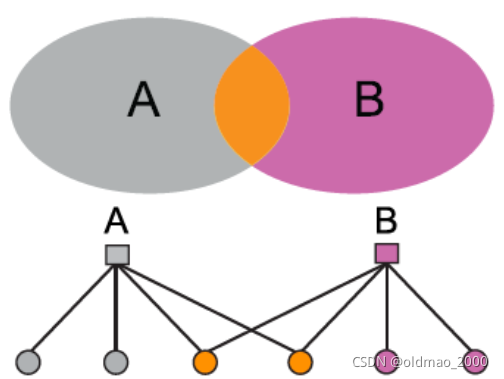
4.Nested
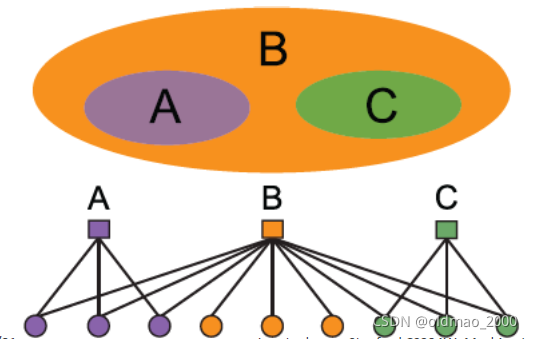
Detecting Communities
反过来从图反推模型(MLE):给定图,找出最大可能生成该图的AGM模型

也就是确定:
M
,
C
,
p
c
M,C,p_c
M,C,pc这些参数使得AGM模型生成给定图G的概率最大化。如果把参数统称为F,则就是要:

这里是图机器学习,所以这个玩意叫图似然。
Graph Likelihood P ( G ∣ F ) P(G|F) P(G∣F)
对于已知的图
G
G
G应该是这个样子(就是邻接矩阵):
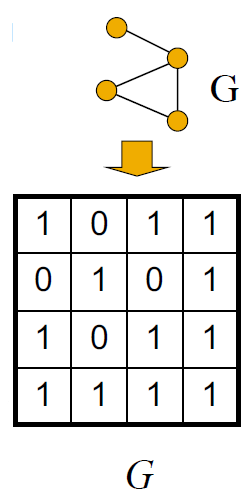
要优化的参数
F
F
F,应该是这个样子(和邻接矩阵大小一样的一个概率矩阵):
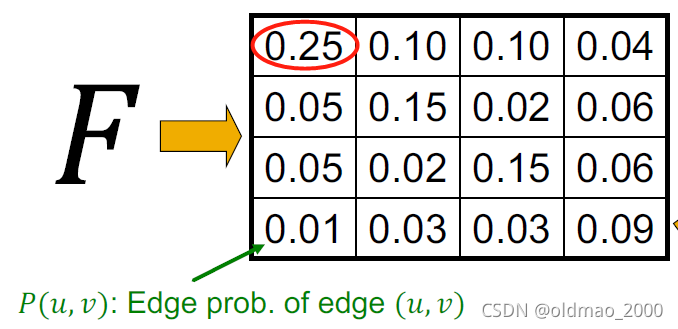
这个矩阵中每个元素代表当前两个节点之间有边的概率,例如红圈里面的0.25表示1号节点和自身产生self-loop的概率是0.25
有了上面两个概念,下面就可以计算:
P
(
G
∣
F
)
P(G|F)
P(G∣F)
上式中第一项表示图 G G G中有边节点对的概率连乘,第二项表示图 G G G中无边节点对的概率连乘
Strengths of Membership
Strengths of Membership定义如下图所示:
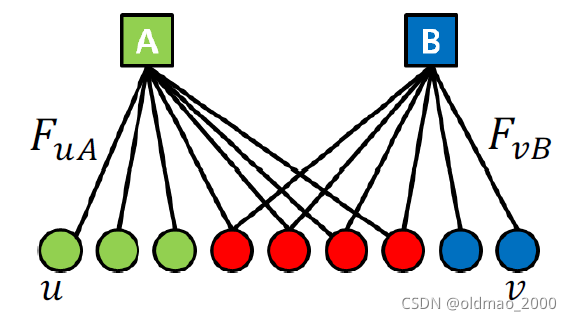
用
F
u
A
F_{uA}
FuA表示节点
u
u
u属于社区
A
A
A的strength,如果
if
u
∉
A
,
F
u
A
=
0
\text{if }u\notin A, F_{uA}=0
if u∈/A,FuA=0
有了这个定义,那么对于某个社区
C
C
C,我们可以用下面的式子来表示两个节点
u
,
v
u,v
u,v相连的概率:
P
c
(
u
,
v
)
=
1
−
exp
(
−
F
u
C
⋅
F
v
C
)
(7)
P_c(u,v)=1-\exp(-F_{uC}\cdot F_{vC})\tag7
Pc(u,v)=1−exp(−FuC⋅FvC)(7)
由于
F
u
C
⋅
F
v
C
≥
0
F_{uC}\cdot F_{vC}\ge 0
FuC⋅FvC≥0,
−
(
F
u
C
⋅
F
v
C
)
≤
0
-(F_{uC}\cdot F_{vC})\le 0
−(FuC⋅FvC)≤0
那么
0
≤
exp
(
−
F
u
C
⋅
F
v
C
)
≤
1
0\le \exp(-F_{uC}\cdot F_{vC})\le 1
0≤exp(−FuC⋅FvC)≤1
因此:
0
≤
P
c
(
u
,
v
)
≤
1
0\le P_c(u,v)\le 1
0≤Pc(u,v)≤1,这个是一个有效概率,例如:
两个报警系统A和B,他们在单独使用时A的有效概率0.92,B的有效概率0.93,
至少有一个有效概率=1-A和B均失效的概率=1-(1-0.92)×(1-0.93)=0.9944
当两个节点
u
,
v
u,v
u,v有一个对社区
C
C
C的strength为0时:
F
u
C
=
0
or
F
v
C
=
0
F_{uC}=0 \text{ or }F_{vC}=0
FuC=0 or FvC=0
则
F
u
C
⋅
F
v
C
=
0
→
exp
(
−
F
u
C
⋅
F
v
C
)
=
1
F_{uC}\cdot F_{vC}=0\rightarrow \exp(-F_{uC}\cdot F_{vC})=1
FuC⋅FvC=0→exp(−FuC⋅FvC)=1
则
P
c
(
u
,
v
)
=
0
P_c(u,v)=0
Pc(u,v)=0
同理,当两个节点
u
,
v
u,v
u,v对社区
C
C
C的strength都很大,这个时候:
P
c
(
u
,
v
)
≈
1
P_c(u,v)\approx 1
Pc(u,v)≈1
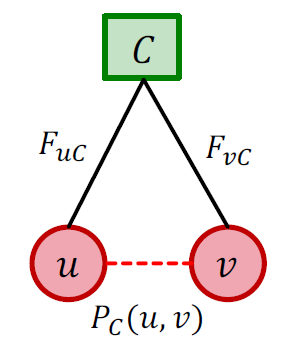
我们把一个节点可以属于多个社区(多个社区集合记为:
Γ
\Gamma
Γ)的设定带进来:
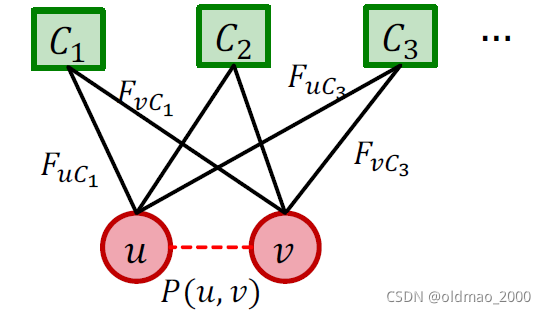
那么两个节点
u
,
v
u,v
u,v通过至少一个社区相连的概率可以写为:
P
(
u
,
v
)
=
1
−
∏
C
∈
Γ
(
1
−
P
C
(
u
,
v
)
)
(8)
P(u,v)=1-\prod_{C\in\Gamma}\left(1-P_C(u,v)\right)\tag8
P(u,v)=1−C∈Γ∏(1−PC(u,v))(8)
这里的
∏
C
∈
Γ
(
1
−
P
C
(
u
,
v
)
)
\prod_{C\in\Gamma}\left(1-P_C(u,v)\right)
∏C∈Γ(1−PC(u,v))就是两个节点
u
,
v
u,v
u,v没有通过任何社区相连的概率的连乘。
将公式7带入8:
P
(
u
,
v
)
=
1
−
∏
C
∈
Γ
(
1
−
P
C
(
u
,
v
)
)
=
1
−
∏
C
∈
Γ
(
1
−
(
1
−
exp
(
−
F
u
C
⋅
F
v
C
)
)
)
=
1
−
∏
C
∈
Γ
exp
(
−
F
u
C
⋅
F
v
C
)
把
exp
计
算
放
到
连
乘
外
面
变
连
加
=
1
−
exp
(
−
∑
C
∈
Γ
F
u
C
⋅
F
v
C
)
(9)
\begin{aligned}P(u,v)&=1-\prod_{C\in\Gamma}\left(1-P_C(u,v)\right)\\ &=1-\prod_{C\in\Gamma}\left(1-(1-\exp(-F_{uC}\cdot F_{vC}))\right)\\ &=1-\prod_{C\in\Gamma}\exp(-F_{uC}\cdot F_{vC})\\ &把\exp计算放到连乘外面变连加\\ &=1-\exp\left(-\sum_{C\in\Gamma}F_{uC}\cdot F_{vC}\right) \end{aligned}\tag9
P(u,v)=1−C∈Γ∏(1−PC(u,v))=1−C∈Γ∏(1−(1−exp(−FuC⋅FvC)))=1−C∈Γ∏exp(−FuC⋅FvC)把exp计算放到连乘外面变连加=1−exp(−C∈Γ∑FuC⋅FvC)(9)
最后把
u
,
v
u,v
u,v节点属于所有社区集合
Γ
\Gamma
Γ的strength写成一个向量:
F
u
:
A vector of
{
F
u
C
}
C
∈
Γ
F
v
:
A vector of
{
F
v
C
}
C
∈
Γ
F_u: \text{A vector of }\{F_{uC}\}_{C\in\Gamma}\\ F_v: \text{A vector of }\{F_{vC}\}_{C\in\Gamma}
Fu:A vector of {FuC}C∈ΓFv:A vector of {FvC}C∈Γ
那么上式9就可以写成两个向量内积是形式:
P
(
u
,
v
)
=
1
−
exp
(
−
F
u
T
⋅
F
v
)
(10)
P(u,v)=1-\exp\left(-F_{u}^T\cdot F_{v}\right)\tag{10}
P(u,v)=1−exp(−FuT⋅Fv)(10)
有了这个结论,下面开始讲具体模型
BigCLAM
公式10表达的意思是
u
,
v
u,v
u,v节点相连的概率正比于节点与社区集合间的strength。
之前有过目标,就是给定图
G
(
V
,
E
)
G(V,E)
G(V,E),需要最大化模型生成图的likelihood(上面用的notation是
(
u
,
v
)
∈
G
(u,v)\in G
(u,v)∈G这里换成E,明白意思即可)
P
(
G
∣
F
)
=
∏
(
u
,
v
)
∈
E
P
(
u
,
v
)
∏
(
u
,
v
)
∉
E
(
1
−
P
(
u
,
v
)
)
P(G|F)=\prod_{(u,v)\in E}P(u,v)\prod_{(u,v)\notin E}(1-P(u,v))
P(G∣F)=(u,v)∈E∏P(u,v)(u,v)∈/E∏(1−P(u,v))
将公式10带入:
P
(
G
∣
F
)
=
∏
(
u
,
v
)
∈
E
(
1
−
exp
(
−
F
u
T
⋅
F
v
)
)
∏
(
u
,
v
)
∉
E
exp
(
−
F
u
T
⋅
F
v
)
P(G|F)=\prod_{(u,v)\in E}\left(1-\exp(-F_{u}^T\cdot F_{v})\right)\prod_{(u,v)\notin E}\exp(-F_{u}^T\cdot F_{v})
P(G∣F)=(u,v)∈E∏(1−exp(−FuT⋅Fv))(u,v)∈/E∏exp(−FuT⋅Fv)
这里老师给了一个解释是我之前没遇到过的,记录一下:
原始的Likelihood涉及到连乘会使得结果非常小(都是小于1的概率相乘),因此很小的变化会使得结果非常不稳定,转化成log后就没有这个问题。
我是根据求解MLE套路就是连乘转连加,直接两边同时求log变成:
log
(
P
(
G
∣
F
)
)
=
log
(
∏
(
u
,
v
)
∈
E
(
1
−
exp
(
−
F
u
T
⋅
F
v
)
)
∏
(
u
,
v
)
∉
E
exp
(
−
F
u
T
⋅
F
v
)
)
=
∑
(
u
,
v
)
∈
E
log
(
1
−
exp
(
−
F
u
T
⋅
F
v
)
)
−
∑
(
u
,
v
)
∉
E
F
u
T
⋅
F
v
(11)
\begin{aligned}\log(P(G|F))&=\log\left(\prod_{(u,v)\in E}\left(1-\exp(-F_{u}^T\cdot F_{v})\right)\prod_{(u,v)\notin E}\exp(-F_{u}^T\cdot F_{v})\right)\\ &=\sum_{(u,v)\in E}\log\left(1-\exp(-F_{u}^T\cdot F_{v})\right)-\sum_{(u,v)\notin E}F_{u}^T\cdot F_{v} \end{aligned}\tag{11}
log(P(G∣F))=log⎝⎛(u,v)∈E∏(1−exp(−FuT⋅Fv))(u,v)∈/E∏exp(−FuT⋅Fv)⎠⎞=(u,v)∈E∑log(1−exp(−FuT⋅Fv))−(u,v)∈/E∑FuT⋅Fv(11)
把11的结果记为我们最后的目标函数
l
(
F
)
\mathcal{l}(F)
l(F)
因为要最大化,所以这里用梯度上升方式来求解,给出对
F
u
F_u
Fu求偏导的结果(就是梯度):
▽
l
(
F
)
=
∑
v
∈
N
(
u
)
(
exp
(
−
F
u
T
⋅
F
v
)
1
−
exp
(
−
F
u
T
⋅
F
v
)
)
⋅
F
v
−
∑
v
∉
N
(
u
)
F
v
\triangledown l(F)=\sum_{v\in \mathcal{N}(u)}\left(\cfrac{\exp(-F_{u}^T\cdot F_{v})}{1-\exp(-F_{u}^T\cdot F_{v})}\right)\cdot F_v-\sum_{v\notin \mathcal{N}(u)}F_v
▽l(F)=v∈N(u)∑(1−exp(−FuT⋅Fv)exp(−FuT⋅Fv))⋅Fv−v∈/N(u)∑Fv
这个梯度的时间复杂度由两部分组成:
第一部分是和节点
u
u
u的度成正比(
v
∈
N
(
u
)
v\in \mathcal{N}(u)
v∈N(u)),速度较快
第二部分和所有节点数量(不含节点
u
u
u及其邻居)成正比(
v
∉
N
(
u
)
v\notin \mathcal{N}(u)
v∈/N(u)),速度较慢
我们把第二部分的计算改成:
∑
v
∉
N
(
u
)
F
v
=
∑
v
F
v
−
F
u
−
∑
v
∈
N
(
u
)
F
v
\sum_{v\notin \mathcal{N}(u)}F_v=\sum_{v}F_v-F_u-\sum_{v\in \mathcal{N}(u)}F_v
v∈/N(u)∑Fv=v∑Fv−Fu−v∈N(u)∑Fv
相当于所有节点的strength减去节点
u
u
u及其邻居集合
N
(
u
)
\mathcal{N}(u)
N(u)的strength。
上式中第一项可以提前计算出来,重复使用,因此整个梯度计算时间复杂度和节点
u
u
u的度呈线性关系。






















 1280
1280











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










