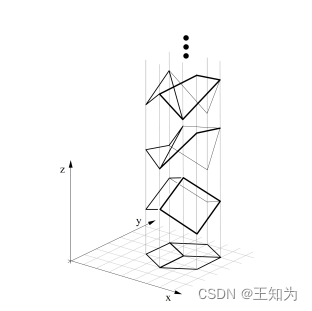
图2.8:任何平面线描绘都在几何上与无限多个3D结构一致。取自[SA93]的图11。获得Pawan Sinha的亲切许可使用。
2.3.3 逆问题 *
概率论涉及根据对世界状态h的了解(或假设)来预测结果y的分布。相比之下,逆概率关注从观察结果中推断世界状态。我们可以将其看作是对h → y映射的反演。
例如,考虑从二维图像y中推断三维形状h,这是视觉场景理解中的经典问题。不幸的是,这是一个根本上不适定的问题,如图2.8所示,因为有多个可能的隐藏h与相同的观察y一致(参见例如[Piz01])。同样,我们可以将自然语言理解视为一个不适定的问题,在这个问题中,听者必须从说话者(通常含糊不清的)说出的话语中推断出意图h(参见例如[Sab21])。
为了解决这类逆问题,我们可以使用贝叶斯定理计算后验概率p(h|y),该后验概率给出了可能的世界状态的分布。这需要指定正向模型p(y|h)以及先验概率p(h),后者可用于排除(或降低权重)不切实际的世界状态。我们将在本书的后续部分,[Mur23]中更详细地讨论这个主题。
2.4 伯努利分布和二项分布
也许最简单的概率分布是伯努利分布,它可用于建模二元事件,如下所述。
2.4.1 定义
考虑抛一枚硬币,它正面朝上的概率为0 ≤ θ ≤ 1。
设Y = 1表示正面朝上的事件,设Y = 0表示硬币正面朝下的事件。因此,我们假设p(Y = 1) = θ,p(Y = 0) = 1 − θ。这被称为伯努利分布,并可以写成如下形式
[ Y \sim \text{Ber}(\theta) ] (2.66)

Figure 2.9: 二项分布的示例,其中N = 10,分别为 (a) θ = 0.25 和 (b) θ = 0.9。由 binom_dist_plot.ipynb 生成。
其中符号 ∼ 表示“从中抽样”或“分布为”,Ber是伯努利的缩写。该分布的概率质量函数(pmf)定义如下:
[ \text{Ber}(y|\theta) = \begin{cases}
1 - \theta & \text{if } y = 0 \
\theta & \text{if } y = 1
\end{cases} ]
(2.67)
(有关pmf的详细信息,请参阅第2.2.1节。)我们可以更简洁地写成:
[ \text{Ber}(y|\theta) = \theta^y (1 - \theta)^{1-y} ]
(2.68)
伯努利分布是二项分布的特例。为了解释这一点,假设我们观察到一组N个伯努利试验,表示为(y_n \sim \text{Ber}(\cdot|\theta)),对于 (n = 1 : N)。具体来说,可以将其看作是N次抛硬币。我们定义 (s) 为正面朝上的总次数,(s = \sum_{n=1}^N I(y_n = 1))。则 (s) 的分布由二项分布给出:
[ \text{Bin}(s|N, \theta) = \binom{N}{s} \theta^s (1 - \theta)^{N-s} ]
(2.69)
其中
[ \binom{N}{k} = \frac{N!}{(N - k)!k!} ]
(2.70)
是从N中选择k个项目的方式数(这称为二项式系数,发音为“N选择k”)。请参见图2.9,了解二项分布的一些示例。如果 (N = 1),则二项分布就变成了伯努利分布。
2.4.2 Sigmoid(逻辑)函数
当我们想要预测一个二元变量 (y \in {0, 1}) ,给定一些输入 (x \in X) 时,我们需要使用以下形式的条件概率分布:
[ p(y|x, \theta) = \text{Ber}(y|f(x; \theta)) ]
(2.71)
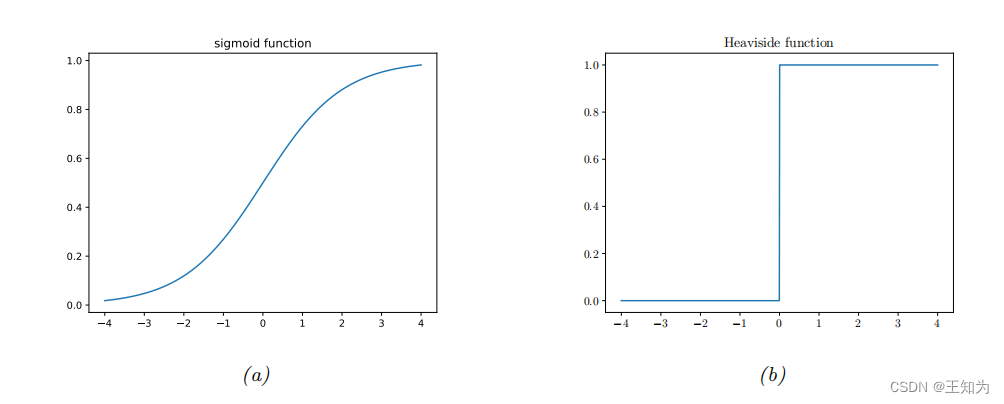
Figure 2.10: (a) Sigmoid(逻辑)函数 (\sigma(a) = (1 + e{-a}){-1})。 (b) Heaviside函数 (I(a > 0))。 由 activation_fun_plot.ipynb 生成。

Table 2.3: Sigmoid(逻辑)及相关函数的一些有用属性。请注意,logit函数是sigmoid函数的反函数,并具有定义域 [0, 1]。
其中 (f(x; \theta)) 是一个函数,用于预测输出分布的均值参数。我们将在第二部分至第四部分考虑许多不同类型的函数 (f)。
为了避免要求 (0 \leq f(x; \theta) \leq 1),我们可以让 (f) 成为一个无约束的函数,并使用以下模型:
[ p(y|x, \theta) = \text{Ber}(y|\sigma(f(x; \theta))) ]
(2.78)
这里 (\sigma()) 是sigmoid或logistic函数,定义如下:
[ \sigma(a) = \frac{1}{1 + e^{-a}} ]
(2.79)
其中 (a = f(x; \theta))。术语“sigmoid”意味着S形状:请参见图2.10a进行绘制。我们可以看到,sigmoid函数的取值范围在(0)和(1)之间。

Figure 2.11: 应用于鸢尾花数据集的一维、两类别版本的逻辑回归。 由 iris_logreg.ipynb 生成。 改编自 [Gér19] 的图4.23。
整个实数线映射到 [0, 1],这对于将输出解释为概率(因此是伯努利参数 θ 的有效值)是必要的。Sigmoid 函数可以被视为“软”版本的阶跃函数,阶跃函数的定义如下:
[H(a) , I(a > 0)]
如图2.10b所示。
将 Sigmoid 函数的定义代入方程 (2.78) 中,我们得到
[p(y = 1|x, θ) = \frac{1}{1 + e^{-a}} = \frac{e^a}{1 + e^a} = \sigma(a)]
[p(y = 0|x, θ) = 1 - \frac{1}{1 + e^{-a}} = \frac{1}{1 + e^a} = \sigma(-a)]
其中 (a) 等于对数几率,log(\left(\frac{p}{1-p}\right)),其中 (p = p(y = 1|x; θ))。为了看到这一点,注意到
[\log \left( \frac{p}{1 - p} \right) = \log \left( \frac{e^a}{1 + e^a} \right) = \log(e^a) = a]
逻辑函数或 Sigmoid 函数将对数几率 (a) 映射到 (p):
[p = \text{logistic}(a) = \sigma(a) = \frac{1}{1 + e^{-a}} = \frac{e^a}{1 + e^a}]
其逆被称为 logit 函数,将 § 映射到对数几率 (a):
[a = \text{logit}§ = \sigma^{-1}§ = \log \left( \frac{p}{1-p} \right)]
有关这些函数的一些有用属性,请参见表2.3。
二元逻辑回归使用条件伯努利模型,其中采用形式为 (f(x; \theta) = w^Tx + b) 的线性预测器。因此,该模型表示为
[p(y|x; \theta) = \text{Ber}(y|\sigma(w^Tx + b))]
(2.86)
换句话说,
[p(y = 1|x; \theta) = \sigma(w^Tx + b) = \frac{1}{1 + e{-(wTx+b)}}]
(2.87)
这被称为逻辑回归。
例如,考虑鸢尾花数据集的一维、两类版本,其中正类是“Virginica”,负类是“非Virginica”,我们使用的特征 (x) 是花瓣宽度。我们对这个数据集拟合了一个逻辑回归模型,并在图2.11中展示了结果。决策边界对应于 (x^) 的值,其中 (p(y = 1|x = x^, \theta) = 0.5)。在这个例子中,我们看到 (x^* \approx 1.7)。
当 (x) 离开这个边界时,分类器对类标的预测变得更加自信。
从这个例子中可以明显看出,为二元分类问题使用线性回归是不合适的。在这样的模型中,随着 (x) 向右移动,概率会增加到超过1,而向左移动则会减少到低于0。
有关逻辑回归的更多细节,请参阅第10章。
2.5 类别分布和多项式分布
为了表示在有限标签集 {1, . . . , C} 上的分布,我们可以使用分类分布,它是对具有 C > 2 个值的伯努利分布的一种推广。
2.5.1 定义
分类分布是具有每个类别一个参数的离散概率分布:
[ \text{Cat}(y|\theta) = \prod_{c=1}^{C} \theta_c^{I(y=c)} ]
换句话说,[ p(y = c|\theta) = \theta_c ]。请注意,参数受到约束,使得 (0 \leq \theta_c \leq 1) 且 (\sum_{c=1}^{C} \theta_c = 1);因此只有 C - 1 个独立参数。
我们可以通过将离散变量 y 转换为具有 C 个元素的 one-hot 向量的方式以另一种方式写出分类分布。其中除了与类别标签对应的条目之外,所有条目都为 0。 (“one-hot” 一词来自电气工程,其中将二进制向量编码为一组导线上的电流,可以是活动的(“hot”)或非活动的(“cold”)。)例如,如果 (C = 3),我们将类别 1、2 和 3 编码为 (1, 0, 0)、(0, 1, 0) 和 (0, 0, 1)。更一般地,我们可以使用单位向量对类别进行编码,其中 (e_c) 除了维度 c 外都是 0。(这也称为虚拟编码。)使用 one-hot 编码,我们可以将分类分布写为:
[ \text{Cat}(y|\theta) = \prod_{c=1}^{C} \theta_c^{y_c} ]
分类分布是多项式分布的特例。为了解释这一点,假设我们观察到 N 次分类试验,(y_n \sim \text{Cat}(\cdot|\theta)),对于 (n = 1 : N)。具体来说,可以将其看作 N 次掷一个 C 面的骰子。我们定义 y 为一个向量,它计算每个面出现的次数,即 (y_c = N_c = \sum_{n=1}^{N} I(y_n = c))。现在 y 不再是 one-hot,而是“multi-hot”,因为它对于在所有 N 次试验中观察到的每个 c 的值都有一个非零的条目。y 的分布由多项式分布给出:
[ M(y|N, \theta) = \frac{N!}{N_1!N_2! \cdots N_C!} \prod_{c=1}^{C} \theta_c^{N_c} ]
其中 (\theta_c) 是面 c 出现的概率,而
[ \frac{N!}{N_1!N_2! \cdots N_C!} ]
是多项式系数,它是将大小为 N = \sum_{c=1}^{C} N_c 的集合分割成大小为 (N_1) 到 (N_C) 的子集的方法的数量。如果 (N = 1),多项式分布就变成了分类分布。
2.5.2 Softmax 函数
在条件情况下,我们可以定义
[ p(y|x, \theta) = \text{Cat}(y|f(x; \theta)) ]
我们还可以写成
[ p(y|x, \theta) = \text{M}(y|1, f(x; \theta)) ]
我们要求 (0 \leq f_c(x; \theta) \leq 1) 且 (\sum_{c=1}^{C} f_c(x; \theta) = 1)。
为了避免 f 直接预测概率向量的要求,通常会将 f 的输出传递到 softmax 函数 [Bri90],也称为多项式 logit。其定义如下:
[ \text{softmax}(a) = \left( \frac{e{a_1}}{\sum_{c=1}{C} e^{a_c}}, \ldots, \frac{e{a_C}}{\sum_{c=1}{C} e^{a_c}} \right) ]

图 2.13: 鸢尾花数据集的三类别、两特征版本上的逻辑回归。改编自 [Gér19] 图 4.25。由 iris_logreg.ipynb 生成。
这将 R^C 映射到 [0, 1]^C,满足 0 ≤ softmax(a)c ≤ 1 和 P{c=1}^{C} softmax(a)_c = 1 的约束。Softmax 函数的输入 a = f(x; θ) 被称为 logits,是 log odds 的一般化。Softmax 函数之所以被这样命名,是因为它有点像 argmax 函数。为了理解这一点,让我们将每个 a_c 除以称为温度的常数 T。然后当 T → 0 时,我们有 softmax(a/T)_c =
{
1.0 if c = argmax_c
0 a_c
0.0 otherwise
也就是说,在低温下,该分布将其大部分概率集中在最有可能的状态(这称为赢者通吃),而在高温下,它将概率均匀地分散。请参见图 2.12 进行说明。
2.5.3 多类别 logistic 回归
如果我们使用形式为 f(x; θ) = Wx + b 的线性预测器,其中 W 是一个 C×D 矩阵,b 是一个 C 维偏置向量,最终模型变为
[ p(y|x; θ) = Cat(y|softmax(Wx + b)) ]
令 a = Wx + b 为 C 维 logits 向量。然后我们可以将上述重写为:
[ p(y = c|x; θ) = \frac{e{a_c}}{\sum_{c’=1}{C} e^{a_{c’}}} ]
这被称为多项 logistic 回归。如果只有两个类别,这将归结为二元 logistic 回归。要理解这一点,注意 softmax(a)_0 =
(\frac{e{a_0}}{e{a_0} + e^{a_1}} = \frac{1}{1 + e^{a_1 - a_0}} = \sigma(a_0 - a_1)),因此我们只需训练模型来预测 a = a_1 - a_0。这可以通过一个单一的权重向量 w 完成;如果使用多类别的形式,我们将有两个权重向量 w_0 和 w_1。这样的模型过于参数化,可能会影响可解释性,但预测将是相同的。
我们将在第10.3节中更详细地讨论这一点。现在,我们只给出一个例子。图2.13显示了当我们将该模型拟合到3类鸢尾花数据集时发生的情况,仅使用了2个特征。我们看到每个类别之间的决策边界是线性的。我们可以通过转换特征(例如,使用多项式)来创建非线性边界,这一点将在第10.3.1节中讨论。
2.5.4 对数求和指数技巧
在本节中,我们讨论在使用 softmax 分布时需要注意的一个重要实际细节。假设我们想计算归一化概率 (p_c = p(y = c|x)),其表示为
[ p_c = \frac{e^{a_c}}{Z(a)} = \frac{e{a_c}}{\sum_{c’=1}{C} e^{a_{c’}}} ]
其中 (a = f(x; θ)) 为 logits。在计算分区函数 Z 时,我们可能会遇到数值问题。例如,假设我们有3个类别,logits 为 (a = (0, 1, 0))。那么我们有 (Z = e^0 + e^1 + e^0 = 4.71)。但是现在假设 (a = (1000, 1001, 1000));我们发现 (Z = ∞),因为在计算机上,即使使用64位精度,np.exp(1000) 也等于 inf。类似地,假设 (a = (-1000, -999, -1000));现在我们发现 (Z = 0),因为 np.exp(-1000) 等于 0。为避免数值问题,我们可以使用以下恒等式:
[ \log \left( \sum_{c=1}^{C} \exp(a_c) \right) = m + \log \left( \sum_{c=1}^{C} \exp(a_c - m) \right) ]
其中 m 可以是任何值。通常使用 (m = \max_c a_c),这确保指数化的最大值将为零,因此绝对不会溢出;即使在下溢时,答案也是合理的。这被称为对数求和指数技巧。我们在实现 lse 函数时使用此技巧:
[ \text{lse}(a) = \log \left( \sum_{c=1}^{C} \exp(a_c) \right) ]
我们可以使用这个技巧从 logits 计算概率:
[ p(y = c|x) = \frac{\exp(a_c - \text{lse}(a))}{\sum_{c’=1}^{C} \exp(a_{c’})} ]
然后,我们可以将其传递给交叉熵损失,该损失在方程(5.41)中定义。
然而,为了节省计算量,并提高数值稳定性,通常修改交叉熵损失,以便将 logits a 作为输入,而不是概率向量 p。例如,考虑二元情况。一个例子的 CE 损失为
[ L = -[I(y = 0) \log p_0 + I(y = 1) \log p_1] ]
其中
[ \log p_1 = \log \left( \frac{1}{1 + \exp(-a)} \right) = \log(1) - \log(1 + \exp(-a)) = 0 - \text{lse}([0, -a]) ]
[ \log p_0 = 0 - \text{lse}([0, a]) ]
2.6 单变量高斯(正态)分布
实数随机变量 (y \in \mathbb{R}) 的最广泛使用的分布是高斯分布,也称为正态分布(关于这些名称的讨论,请参见第2.6.4节)。
2.6.1 累积分布函数
我们定义连续随机变量 Y 的累积分布函数(CDF)如下:
[ P(y) \quad \text{or} \quad Pr(Y \leq y) \quad (2.106) ]
(请注意我们使用大写 P 表示 CDF。)使用这个定义,我们可以计算处于任何区间的概率如下:
[ Pr(a < Y \leq b) = P(b) - P(a) \quad (2.107) ]
CDF 是单调不减函数。
高斯的 CDF 由下式定义:
[ \Phi(y; \mu, \sigma^2) = \int_{-\infty}^{y} \mathcal{N}(z | \mu, \sigma^2) , dz \quad (2.108) ]
参见图2.2a以获取绘图。请注意,高斯的 CDF 通常使用 (\Phi(y; \mu, \sigma^2) = \frac{1}{2} [1 + \text{erf}(z/\sqrt{2})]) 实现,其中 (z = (y - \mu)/\sigma),erf(u) 是误差函数,定义为
[ \text{erf}(u) = \frac{1}{\sqrt{2\pi}} \int_{0}^{u} e{-t2} , dt \quad (2.109) ]
参数 (\mu) 编码分布的均值;在高斯的情况下,这也是众数。参数 (\sigma^2) 编码方差。(有时我们谈论高斯的精度,即逆方差,用 (\lambda = 1/\sigma^2) 表示。)当 (\mu = 0) 且 (\sigma = 1) 时,高斯称为标准正态分布。
如果 P 是 Y 的 CDF,那么 (P^{-1}(q)) 是值 (y_q),使得 (p(Y \leq y_q) = q);这被称为 P 的第 q 个分位数。值 (P^{-1}(0.5)) 是分布的中位数,左侧有一半的概率质量,右侧有一半。值 (P^{-1}(0.25)) 和 (P^{-1}(0.75)) 是下四分位数和上四分位数。
例如,设 Φ 是高斯分布 N(0, 1) 的 CDF,Φ^{-1} 是反函数(也称为 probit 函数)。然后,在 Φ^{-1}(α/2) 左侧的点包含 α/2 的概率质量,如图2.2b所示。由对称性,Φ^{-1}(1 - α/2) 右侧的点也包含 α/2 的质量。因此,中心区间 ((\Phi^{-1}(α/2), \Phi^{-1}(1 - α/2))) 包含 1 - α 的质量。如果我们设置 α = 0.05,则中心 95% 区间由范围 ((\Phi^{-1}(0.025), \Phi^{-1}(0.975)) = (-1.96, 1.96)) 覆盖。
如果分布是 N(µ, σ^2),则95%区间变为 ((\mu - 1.96\sigma, \mu + 1.96\sigma))。这通常近似为写作 (\mu \pm 2\sigma)。
2.6.2 概率密度函数
我们将概率密度函数(PDF)定义为累积分布函数的导数:
[ p(y) \quad \text{or} \quad \frac{d}{dy}P(y) \quad (2.111) ]
高斯的 PDF 给出为
[ \mathcal{N}(y | \mu, \sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}} e{-\frac{1}{2\sigma2}(y-\mu)^2} \quad (2.112) ]
其中 (\sqrt{2\pi\sigma^2}) 是确保密度积分为1所需的规范化常数(参见练习2.12)。请参见图2.2b以获取绘图。
给定 PDF,我们可以计算连续变量处于有限区间的概率如下:
[ Pr(a < Y \leq b) = \int_{a}^{b} p(y) , dy = P(b) - P(a) \quad (2.113) ]
随着区间大小变得更小,我们可以写成
[ Pr(y \leq Y \leq y + dy) \approx p(y) , dy \quad (2.114) ]
直观地说,这表示 Y 处于 y 周围的小区间的概率是 y 处的密度乘以区间的宽度。以上结果的一个重要结论是,点上的 PDF 可能大于1。例如,(\mathcal{N}(0|0, 0.1) = 3.99)。
我们可以使用 PDF 计算分布的均值或期望值:
[ E[Y] = \int_{-\infty}^{\infty} y , p(y) , dy \quad (2.115) ]
对于高斯分布,我们有熟悉的结果,即 (E[\mathcal{N}(·|\mu, \sigma^2)] = \mu)。(然而,请注意,对于某些分布,这个积分是无限的,因此均值未定义。)
我们还可以使用 PDF 计算分布的方差。这是“扩展”的度量,通常用 (\sigma^2) 表示。方差定义如下:
[ V[Y] = E[(Y - \mu)^2] = \int_{-\infty}^{\infty} (y - \mu)^2 , p(y) , dy \quad (2.116) ]
[ = \int_{-\infty}^{\infty} y^2 , p(y) , dy + \mu^2 \int_{-\infty}^{\infty} p(y) , dy - 2\mu \int_{-\infty}^{\infty} y , p(y) , dy ]
[ = E[Y^2] - \mu^2 \quad (2.117) ]
从中我们得到了一个有用的结果
[ E[Y^2] = \sigma^2 + \mu^2 \quad (2.118) ]
标准差定义为
[ \text{std}[Y] = \sqrt{V[Y]} = \sigma \quad (2.119) ]
(标准差可能比方差更易解释,因为它具有与 Y 本身相同的单位。)对于高斯分布,我们有熟悉的结果,即 (\text{std}[\mathcal{N}(·|\mu, \sigma^2)] = \sigma)。

Figure 2.14: 使用高斯输出的线性回归,其中均值 (\mu(x) = b + wx),(a) 固定方差 (\sigma^2)(同方差)或 (b) 输入相关方差 (\sigma(x)^2)(异方差)。由 linreg_1d_hetero_tfp.ipynb 生成。
2.6.3 回归
到目前为止,我们一直考虑无条件的高斯分布。在某些情况下,将高斯的参数作为某些输入变量的函数是有帮助的,即,我们想要创建形式为
[ p(y|x; \theta) = \mathcal{N}(y|f_{\mu}(x; \theta), f_{\sigma}(x; \theta)^2) ]
其中 (f_{\mu}(x; \theta) \in \mathbb{R}) 预测均值,而 (f_{\sigma}(x; \theta)^2 \in \mathbb{R}^+) 预测方差。
通常,我们假设方差是固定的,并且与输入无关。这称为同方差回归。此外,通常假设均值是输入的线性函数。得到的模型称为线性回归:
[ p(y|x; \theta) = \mathcal{N}(y|w^Tx + b, \sigma^2) ]
其中 (\theta = (w, b, \sigma^2))。见图 2.14(a) 以了解此模型在 1d 中的示意图,并参阅第 11.2 节以了解此模型的更多详细信息。
然而,我们还可以使方差取决于输入;这被称为异方差回归。在线性回归设置中,我们有
[ p(y|x; \theta) = \mathcal{N}(y|w_{\mu}^Tx + b, \sigma_+(w_{\sigma}^Tx)) ]
其中 (\theta = (w_{\mu}, w_{\sigma})) 是两种形式的回归权重,而
[ \sigma_+(a) = \log(1 + e^a) ]
是 softplus 函数,将从 \mathbb{R} 到 \mathbb{R}^+ 映射,以确保预测的标准差为非负数。见图 2.14(b) 以了解此模型在 1d 中的示意图。
请注意,图 2.14 绘制了 95% 的预测区间,([\mu(x) - 2\sigma(x), \mu(x) + 2\sigma(x)])。这是给定 x 的预测观测 y 的不确定性,捕获了蓝色点的变异性。相比之下,底层(无噪声)函数的不确定性由 (p V[f_{\mu}(x; \theta)]) 表示,它不涉及 (\sigma) 项;现在的不确定性是关于参数 (\theta),而不是输出 y。有关如何建模参数不确定性的详细信息,请参见第 11.7 节。
2.6.4 为什么高斯分布被如此广泛使用?
高斯分布是统计学和机器学习中最广泛使用的分布。这有几个原因。首先,它有两个易于解释的参数,捕捉了分布的一些最基本的特性,即其均值和方差。其次,中心极限定理(第 2.8.6 节)告诉我们,独立随机变量的和具有近似的高斯分布,使其成为对残差错误或“噪声”建模的良好选择。第三,高斯分布在满足具有指定均值和方差的约束的同时,做出了最少数量的假设(具有最大熵),如我们在第 3.4.4 节中所示;这使其成为许多情况下的良好默认选择。最后,它具有简单的数学形式,导致易于实施但通常非常有效的方法,正如我们将在第 3.2 节中看到的。
从历史的角度来看,值得注意的是,“高斯分布”这个术语有点误导,因为正如 Jaynes [Jay03, p241] 所指出的:“当高斯六岁时,拉普拉斯注意到了这个分布的基本特性和主要性质;而在拉普拉斯出生之前,de Moivre 就已经发现了这个分布本身。”然而,高斯在 19 世纪推广了该分布的使用,并且“高斯”这个术语现在在科学和工程中被广泛使用。术语“正态分布”似乎是与线性回归中的正态方程有关的(参见第 11.2.2.2 节)。然而,我们更倾向于避免使用术语“正态”,因为它暗示其他分布是“非正常的”,而正如 Jaynes [Jay03] 指出的,实际上是高斯在某种意义上是非正常的,因为它具有许多一般分布不具有的特殊性质。
2.6.5 作为极限情况的狄拉克δ函数
当高斯的方差趋近于 0 时,分布趋近于均值处的一个无限窄但无限高的“尖峰”。我们可以写成:
[ \lim_{\sigma \to 0} \mathcal{N}(y|\mu, \sigma^2) \to \delta(y - \mu) ]
其中 (\delta) 是狄拉克δ函数,定义为:
[ \delta(x) = \begin{cases} +\infty & \text{if } x = 0 \ 0 & \text{if } x \neq 0 \end{cases} ]
其中
[ \int_{-\infty}^{\infty} \delta(x) ,dx = 1 ]
这的一个变体是定义
[ \delta_y(x) = \begin{cases} +\infty & \text{if } x = y \ 0 & \text{if } x \neq y \end{cases} ]
请注意我们有
[ \delta_y(x) = \delta(x - y) ]
Delta函数分布满足以下的筛选性质,我们将在后面用到:
[ \int_{-\infty}^{\infty} f(y) \delta(x - y) , dy = f(x) ] (方程 2.129)
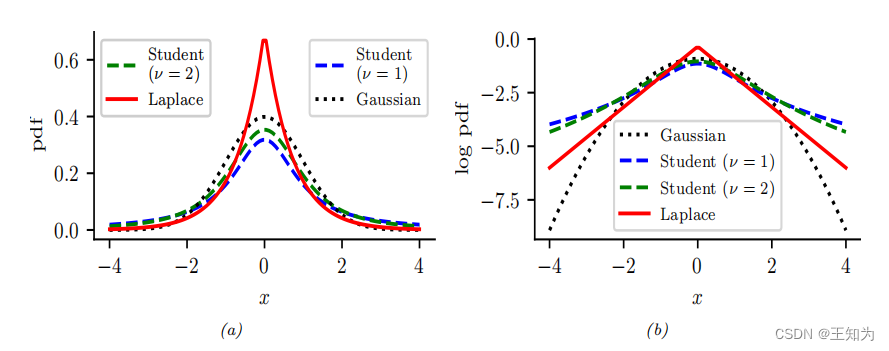
Figure 2.15: (a) 对于 (N(0, 1))、(T(\mu = 0, \sigma = 1, \nu = 1))、(T(\mu = 0, \sigma = 1, \nu = 2)) 和 Laplace(0, (1/\sqrt{2})),显示了它们的概率密度函数(pdf)。高斯和拉普拉斯都具有均值 0 和方差 1。当 (\nu = 1) 时,学生 t 分布与柯西分布相同,它没有明确定义的均值和方差。(b) 这些概率密度函数的对数。请注意,学生 t 分布对于任何参数值都不是对数凹函数,与拉普拉斯分布不同。尽管如此,两者都是单峰的。由 student_laplace_pdf_plot.ipynb 生成。

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










