[浙大机器学习课程] 支持向量机求解转化为数学最优化问题

背景

对浙大《机器学习》课程，支持向量机部分的一点消化。对应2.1.1, 2.2.1, 2.3.1。

支持向量机求解

对于一个线性可分的训练样本集，支持向量机就是要找出一个超平面。这个超平面满足：

1. 这个超平面分开了训练样本集
2. 该超平面有最大的间隔(margin)
   • 课程里原话是这么说的。我觉得准确说应该是：由该超平面推出的两边两个支持向量之间有最大的距离。
3. 该超平面处于间隔的中间，到所有支持向量的距离相等。
   

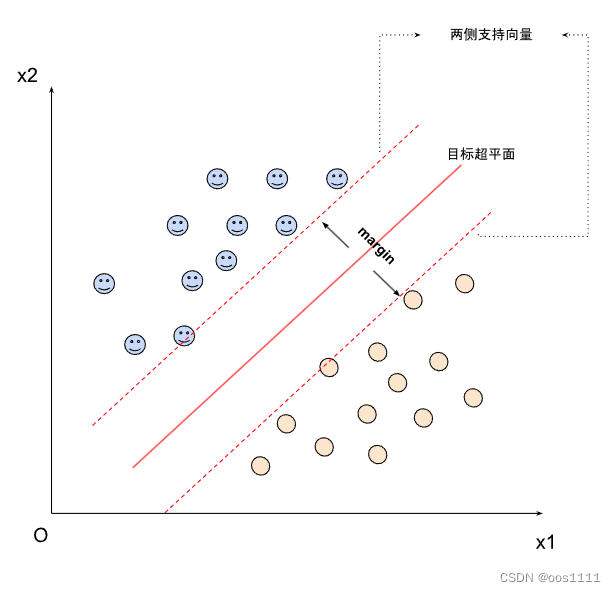
线性可分的定义

对于样本集$\{(X_i,y_i),i=\mathrm{1...}N\}$，存在超平面 ${\omega }^T\cdot X+b=0$，使得：

• y = -1 时，${\omega }^T\cdot X+b<0$

• y = 1 时，${\omega }^T\cdot X+b>0$

转化为数学最优化问题

最小化 $\frac{1}{2}{\Vert \omega \Vert }^2$，使得 $y_i($