【机器学习·浙江大学】机器学习概述、支持向量机SVM（线性模型）

机器学习概述

机器学习

• 特征提取(feature)

• 根据提取的特征构造算法，实现特定的任务⭐（这门课程的重点：假设所有的特征已经存在且有效，如何根据这些特征来构造学习算法）

• 如下图所示，机器学习主要就是来进行如何画这一条线（也就是模型，即从泛指从数据中学习得到的结果，其对应了关于数据的某种潜在的规律，因此称为“假设”；这种潜在规律自身，则称为“真相”或者“真实”ground-truth，学习得到模型的过程，就是去找出或者逼近真相）：
  

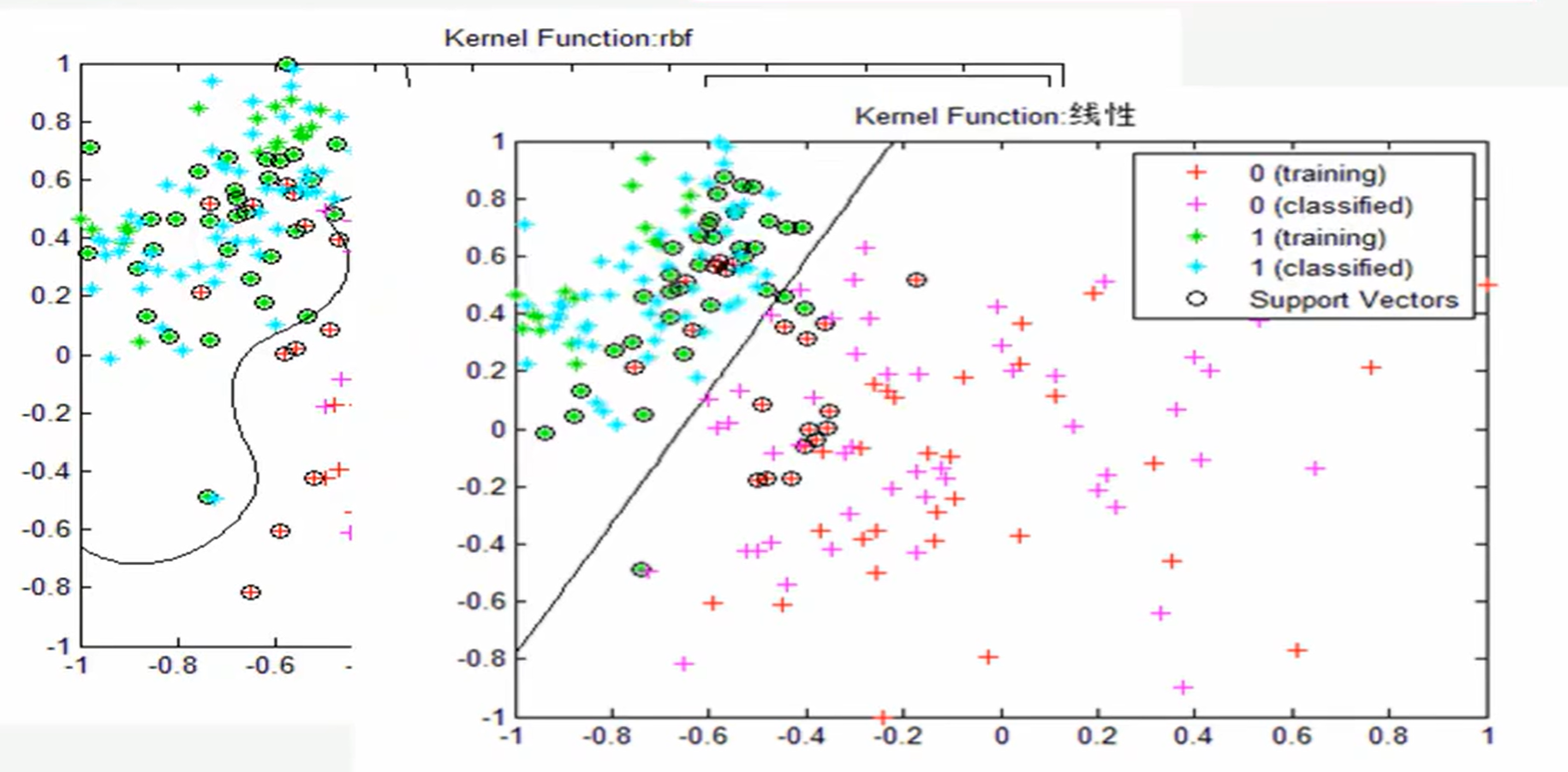
• 难点

  • 维度（超平面hyper plane上万维度，如何去做这样一个超平面->困难
  • 标准：那一条曲线or哪一个超平面是最好的（没有同一的标准，不同算法的画线和判别标准不同（而机器学习就是学习这些不同的算法，对这些算法有一个感觉，适用于什么场景

• 没有免费午餐定理
  如果我们不对特征空间进行先验假设，则所有算法的平均表现一样（农场主理论），有了先验假设，才可以说哪个算法更好！

• 几乎所有机器学习的算法所做的事情都可以分为以下三步

  • 首先用一个方程or一个复杂的函数（其实本质上神经网络就是一个很复杂的函数）来限定一个模型
  • 在这个模型中，留出一些待定的参数
  • 利用样本，去训练模型，用相应的算法去确定待定参数（关键）

所以在对比算法时，往往也可以从这三方面来进行对比。

0、历史沿革

• 发明者：Vapnic（苏联人）
• 发明时间：70年代中期
• 发表时间：苏联解体后，Vapnic去往美国，在90年代将其发表
• 算法性质：针对小样本问题
• 理论支撑：完整&优美的数学理论

一、线性模型、SVM的基本思想

🌸什么是线性模型？
  在上文的机器学习概述中，我们知道，机器学习的核心就是在特征空间中画这样一个线or面，把训练数据给划分开。而线性模型，其实直观上来讲，就是这个线是直线or这个面是一个超平面，这样的模型我们称为线性模型：

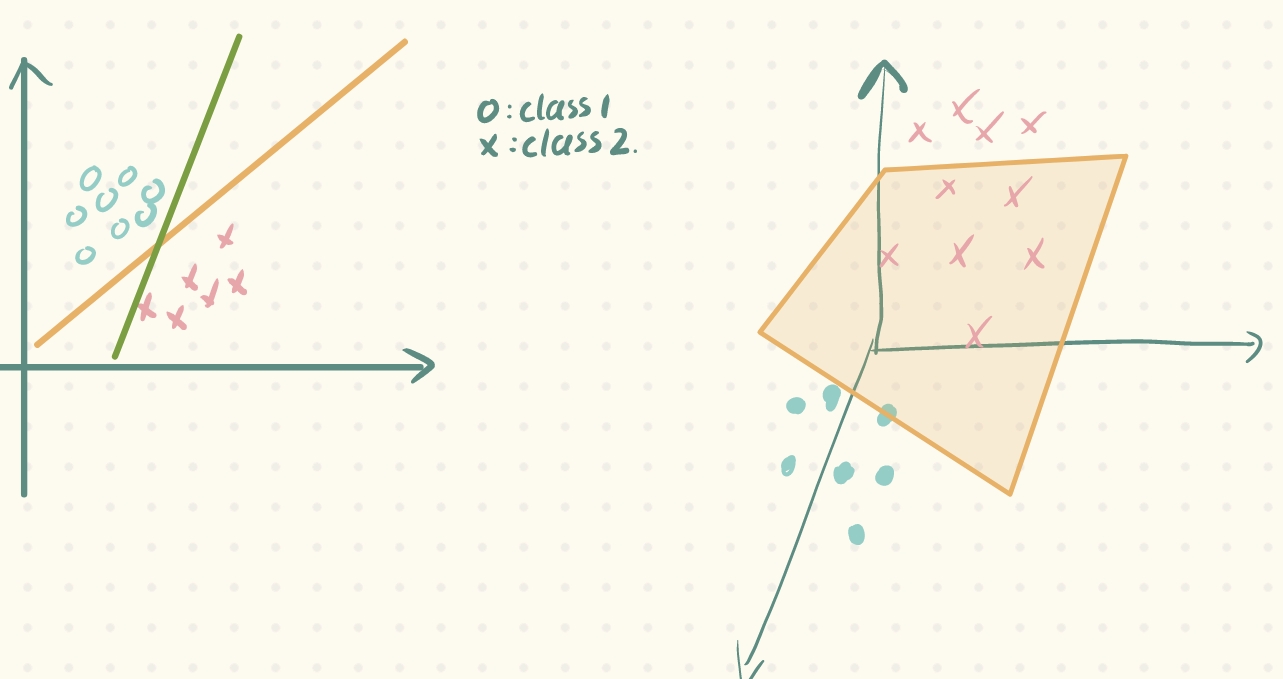
  同时，对于这样的训练样本集我们称为线性可分训练样本集（Linear Separable)；相反，若无法画一条直线or超平面对训练样本集进行划分，则该样本集称为非线性可分训练样本集(Non-Linear Seperable)。

 💁🏻‍♀️而SVM（support vector machine）则是研究，如何在线性可分训练样本集上画这样一条直线or超平面，进而推广到非线性可分训练样本集。

🌸哪一条直线（模型）是最好的？——模型的评判标准（SVM的基本思想）

  如果存在一条直线可以将样本集进行划分，那么必然存在无数条直线可以对其进行划分。那么哪一条直线是最好的呢？

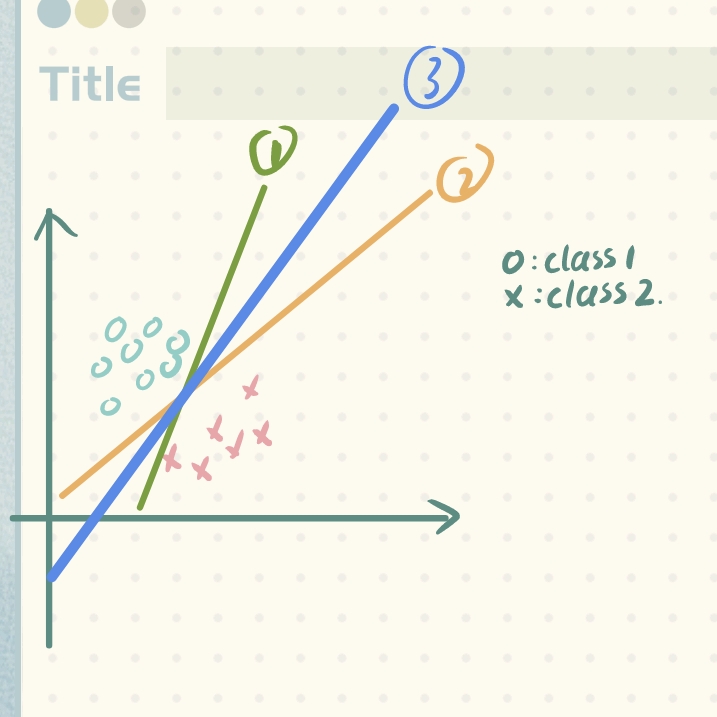
  根据上面概述中讲到的“没有午餐定理”，其实并不存在什么“最好”的模型，除非对特征空间进行假设(hypothesis)，这种假设也是 基于先验知识（训练数据）的某种潜在的规律。
  根据我们的先验知识，从我们角度出发，相信很多人都会在下面三条直线中选择②号线：

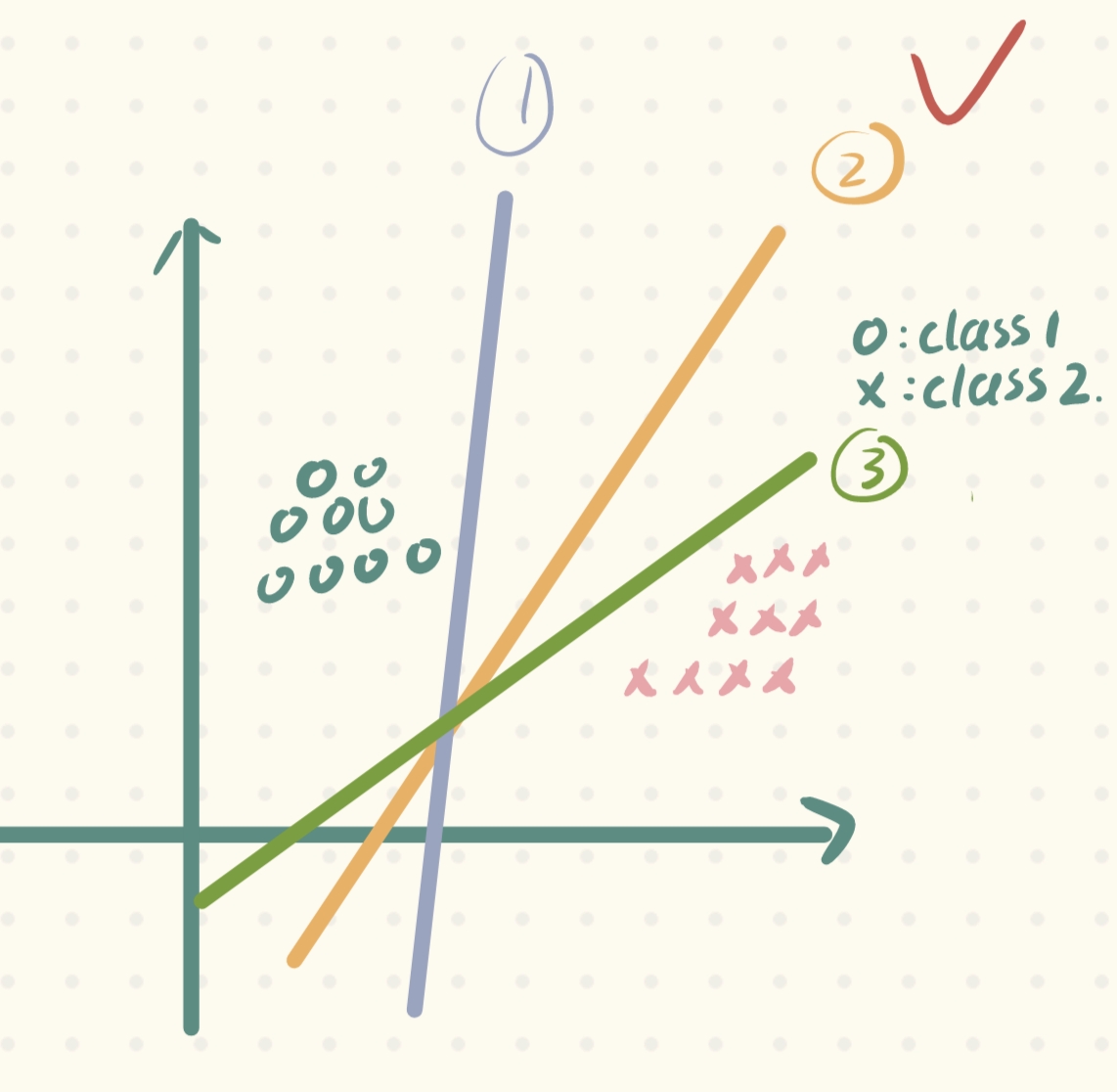
  为什么呢？这其实是根据我们的先验知识或者说是假设（潜在的规律），如下图，只有②号线它的容错能力是最强的（这种容错能力也称为泛化性，当新样本来临时，它的表现会更好），因此我们选择它：

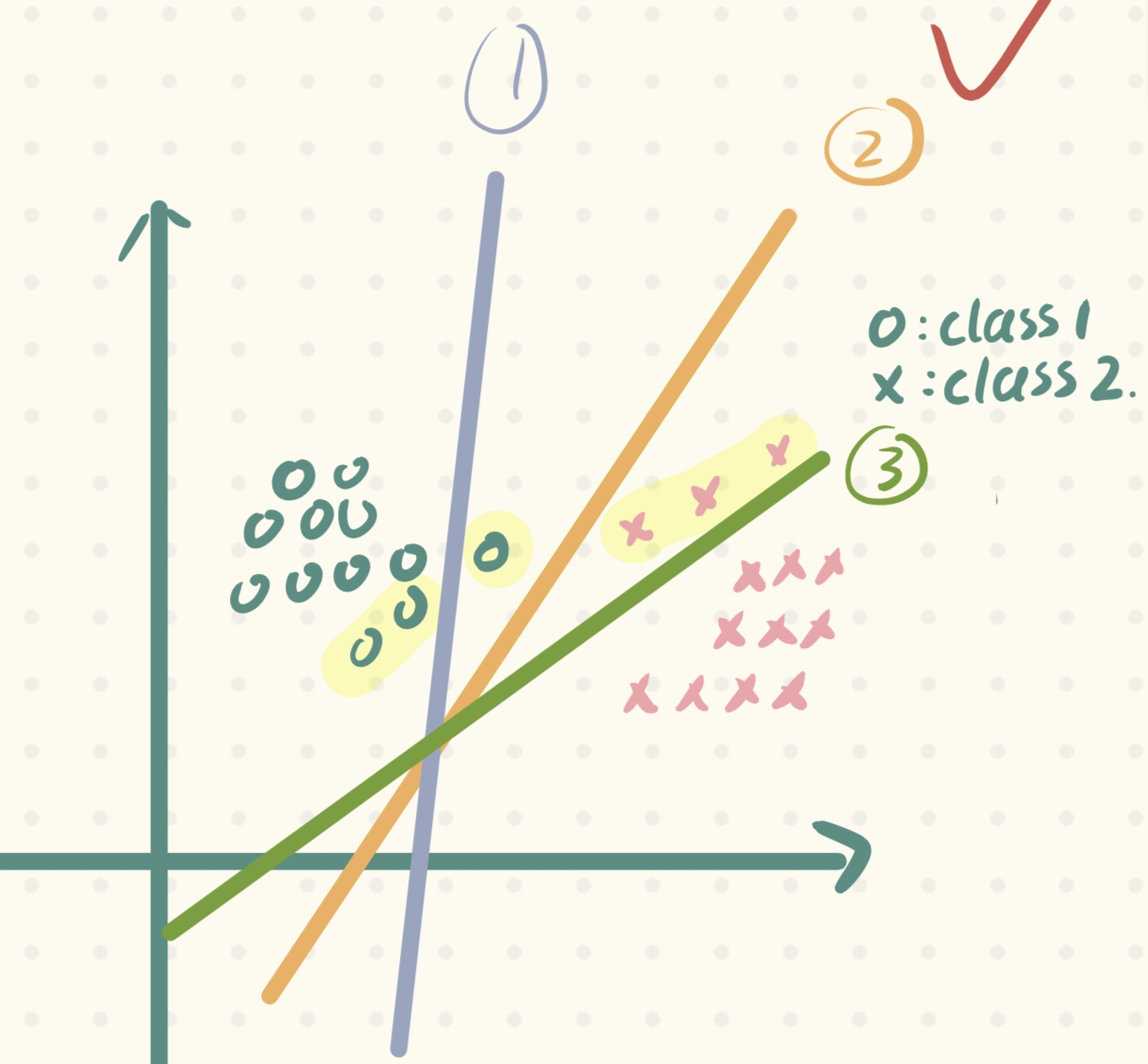
  那么如何以描述这种假设呢？Vapnic做出如下假设：
   1. 首先我们需要定义对每条直线的一个评判/衡量的标准：performance-measure 代表这条直线的 性能指标，且每条直线都可以计算出其相应的performance
   2. 当然，我们要保证那个容错性能最好的直线的performance是最大的。那么如何计算直线的性能指标呢？对每条直线进行平移，直到穿过每个类别的一个or几个点为止，计算出平移距离之和（也就是间隔），间隔d最大的那条直线，就是我们要选取的那条直线。（同时还有一个约束条件：保证这条线在这个距离之间，即d/2的位置，这样才能保证这条直线唯一）。

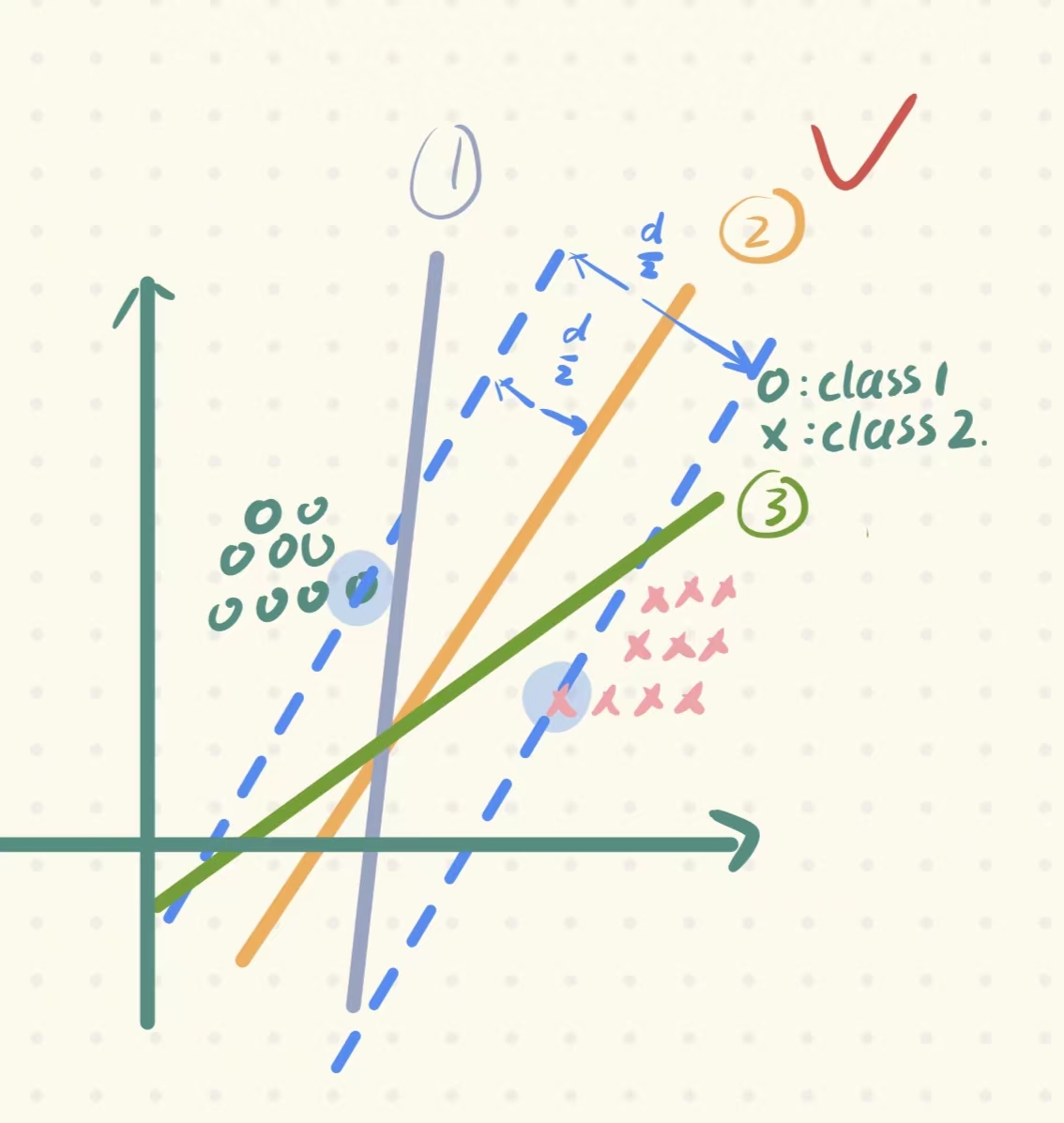
💁🏻‍♀️其实上面的定义性能指标、计算性能指标的过程，就是SVM的基本思想。那么如何对这个过程用数学形式进行表示呢？

二、SVM的数学描述

2.1：一些定义

1. d：间隔/间隔距离（margin)——支持向量机就是最大化margin的方法

2. 将直线上下移动所穿过的向量称为：支持向量（support vectors)——为什么呢？因为我们从上文讲到的确定最终直线的方法来看，最大化距离、确定直线，只和这几个穿过的支持向量有关（这也是为什么SVM适合小样本问题）

   

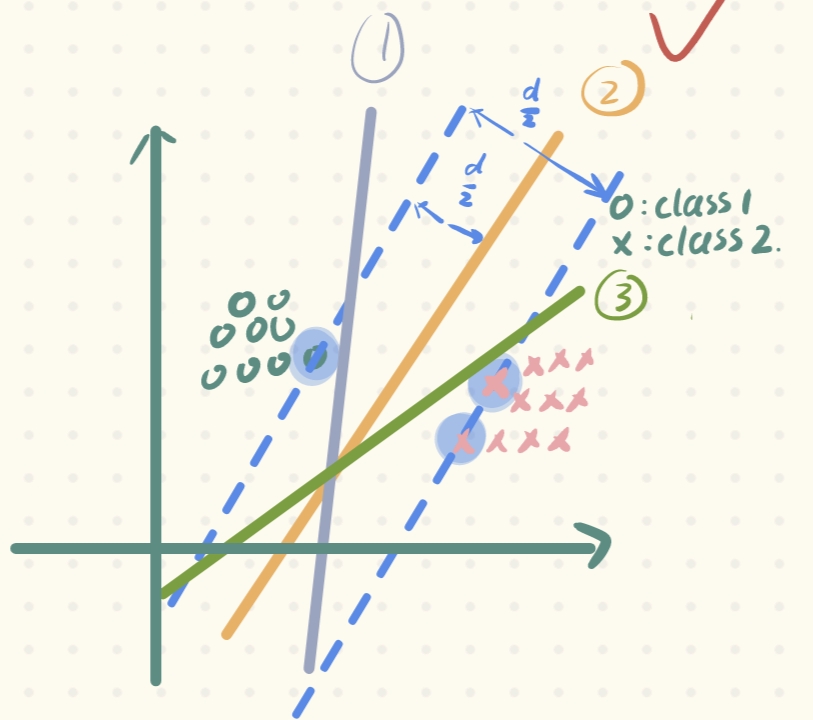
3. 训练数据及其标签：$({\overrightarrow{X}}_1,y_1)$，$({\overrightarrow{X}}_2,y_2)$，$({\overrightarrow{X}}_3,y_3)$…$({\overrightarrow{X}}_N,y_N)$

   注意：$\overrightarrow{X}$是特征向量；在这里我们讨论的是二分类问题，$y$ 我们限定只能取-1和1，代表为两个类别。

4. 线性模型：

   • 参数：$(\overrightarrow{W},b)$
   • 超平面（线性模型）的表达：${\overrightarrow{W}}^T\cdot \overrightarrow{X}+b=0$

5. 一个训练样本集线性可分是指：对于样本集 { ( X i , y i ) } i = 1 … N \left \{ (X_{i},y_{i} )\right \}_{i=1\dots N} {(Xi​,yi​)}i=1…N​
   存在$(W,b)$，使得，对任意$({\overrightarrow{X}}_i,y_i)$ 有：

   • 若$y_i=+1$，则${\overrightarrow{W}}_i^T\cdot \overrightarrow{X}+b\ge 0$
   • 若$y_i=-1$，则${\overrightarrow{W}}_i^T\cdot \overrightarrow{X}+b<0$

   上述两个式子合起来也可以用一个公式来表示： $y_i({\overrightarrow{W}}_i^T\cdot \overrightarrow{X}+b)>0$

   就是存在一个超平面可以将其划分开，使得一类数据在该平面的一侧，另外一类在另一侧，只不过上面是数学表示罢了。

2.2：SVM的优化问题

 上文讲到SVM的线性模型（也就是那个划分样本集的超平面），该如何确定呢？这个问题也叫做SVM的优化问题。其实在第一节讲SVM的基本思想时，我们已经窥得许多了，它的核心就是最大化间隔(margin)——d。在这里，我们将表述成更简洁更优雅的数学表示（本质是做了一个优化，从而确定参数w,b，但是背后的原理还是从最小化d触发的）：

• 最小化（minimize）：${\Vert W\Vert }^2$
• 限制条件 (subject to）：$y_i({\overrightarrow{W}}_i^T\cdot \overrightarrow{X}+b)\ge 1（i=1\dots N）$

 用一句话来解释一下，就是在上面的限制条件下，对${\Vert W\Vert }^2$进行最小化

 相信你和我一样，是不是感到莫名其妙，明明我们的侧重点是放在间隔d，间隔d应该相等且最大，怎么现在突然扯到W上了？不急，我们现在慢慢道来。

 首先我们要明确两个事实：

1. ${\overrightarrow{W}}^T\cdot \overrightarrow{X}+b=0$ 和 $a{\overrightarrow{W}}^T\cdot \overrightarrow{X}+ab=0$ 是一个平面，$a\in R^{+}$.这说明：若$(W,b)$ 满足线性模型，则$(aW,ab)$也满足。
2. 向量 $X_0$ 到超平面 ${\overrightarrow{W}}^T\cdot \overrightarrow{X}+b=0$ 的距离为：$d=\frac{|W^T\cdot X_0+b|}{{\Vert W\Vert }^2}$

 OK ，根据事实2，我们得到了间隔d的表达式，但是我们也发现， 直接让所有的支持向量的d最大，是一个很难操控的事情，如是，我们做了如下转换：

 我们根据事实1， 使用一个正实数a对参数进行如下缩放：
$$(W,b)\to (aW,ab)$$
 最终使得所有的支持向量$X_0$,有：$|W^T\cdot X_0+b|=1$，此时，$d=\frac{1}{{\Vert W\Vert }^2}$，至此，为什么要最小化${\Vert W\Vert }^2$也就显而易见了。

 当然，只最大化d从而最小化w可不行，那平面可以无限远呀，那不就最大了。所以还要需要限制条件，保证其他非支持向量的向量点能被成功划分开，这也是为什么有那个限制条件。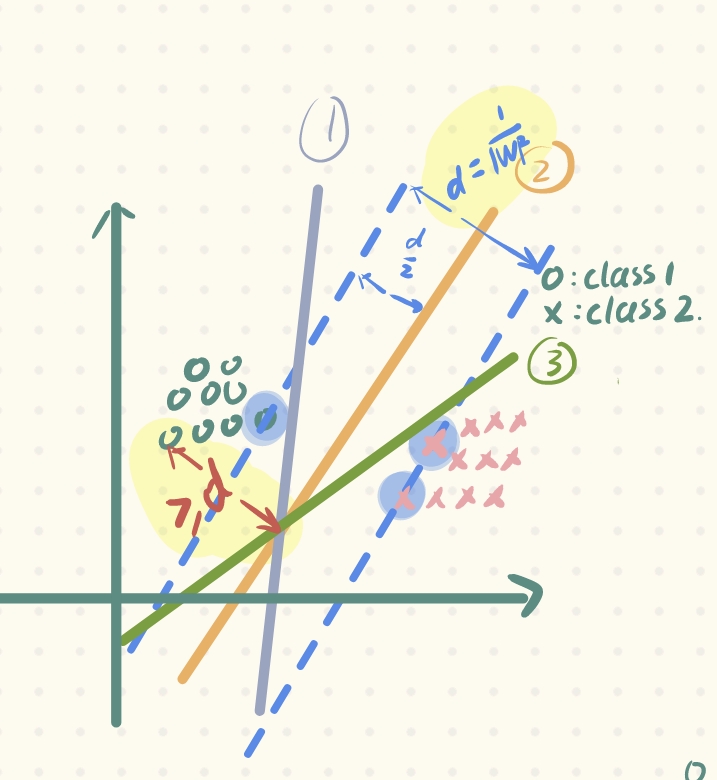

🪧 扩展：

• 首先，有一些教材会在“最小化”那里，写成$\frac{{\Vert W\Vert }^2}{2}$，其实没什么区别，就是为了求导时能消去W头上移下来的2。
• 其次，在限制条件那里，其实 $y_i({\overrightarrow{W}}_i^T\cdot \overrightarrow{X}+b)$ 可以大于任何正实数，道理很简单，因为a可以取不同正实数，且代表的还是同一个平面。

最后，就是如何确定参数W呢？这里其实是 凸优化（二次规划） 问题，也是我们常听说的梯度下降法，不断试探直到达到最优点。

三、SVM和逻辑回归（LR）的对比

关于逻辑回归在前面的博客中已经讲解过，感兴趣的同学可以去了解一下【吴恩达·机器学习】第三章：分类任务：逻辑回归模型（交叉熵损失函数、决策边界、过拟合、正则化）。这里我想将两者进行比较，因为在我学习的过程中，我就发现这两者似乎非常相像。

💐 LR和SVM的相同点

• 都是监督学习算法（都需要有样本进行训练）
• 如果不考虑核函数，LR和SVM都是线性分类算法
• 都是判别模型（判别模型会生成一个表示 P(y|x) 的判别函数）

💐 LR和SVM的不同点

• 损失函数不同：LR采用对对数损失函数,SVM采用hinge损失函数（所谓损失函数，就是我们最终想要最小化的那个东西！）
• SVM损失函数自带正则项，LR必须另在损失函数上添加正则项
• SVM 只考虑局部的分界线附近的点（支持向量），LR考虑全局（每个样本点都必须参与决策面的计算过程）

  其实SVM也考虑了其他点，在限制条件里，只不过影响效果没有那么大，这也是下面一点要说的

• LR对异常值敏感，SVM对异常值不敏感
• 在解决非线性问题时，SVM采用核函数机制，而LR通常不采用核函数的方法（SVM只有几个样本点参与核计算，而LR如果要使用核函数，则所有样本点都要参与核计算，计算复杂度太高，不划算）
• 线性SVM依赖数据表达的距离测度，所以需要对数据先做normalization，LR不受影响。（线性SVM寻找最大间隔分类器时是依据数据的距离测量的，如果不对数据进行正则化，会对结果有所影响，然而，LR虽然也会用到正则化，却是为了方便优化过程的起始值，LR求解的过程是与距离测量无关的，所以归一化对于LR的求解结果是没有影响的）

上面说实话是我在网上找到的，说的不无道理，下面我想说说我理解的不同点。首先你可能还记得在上文机器学习概述中讲到的，几乎所有机器学习的算法所做的事情都可以分为以下三步

1. 首先用一个方程or一个复杂的函数（其实本质上神经网络就是一个很复杂的函数）来限定一个模型
2. 在这个模型中，留出一些待定的参数
3. 利用样本，去训练模型，用相应的算法去确定待定参数（关键）

OK，我们从这三点来对比一下SVM和LR

1. 限定模型：都是线性模型——相同
2. 预留参数：都是(W,b)——相同
3. 确定参数的方法——不同
   a. LR：采用的是最大似然估计方法，我们的目标是求取最大化对数似然函数的参数值，这个过程通常使用梯度下降法或牛顿法等优化算法实现。
   b. SVM：采用的是间隔最大化策略，其目标是寻找一个划分超平面，使得该平面距离最邻近的训练样本点（即支持向量）的距离最大化，求解过程一般通过二次规划求解器完成。

其实本质也是我们在“没有免费午餐定理”中提到的，它们两个的“假设”不同：LR旨在最大化样本的似然概率（也即让模型尽可能拟合每一个样本），而SVM在保证分类正确的前提下，尽可能找到离分隔面最远的边界，以实现对未知样本最好的分类效果（容错性）。