OpenModelica仿真RLC电路

前几天课程设计做电机仿真要用MATLAB,当时想找有没有Python做的类似simulink的程序，后来就找到了OpenModelica，模型是用建模语言modelica写的，查看了modelica的官网才知道Wolfram旗下的SystemMolder也是基于modelica做出来的，之前接触过一下，而OpenModelica是开源免费的，其功能也非常强大，刚学习不久，这里就写下短文记录一下

安装

官网下载，多个平台（LINUX、WIN、MAC)均有，本人的安装环境是WIN 64.

本来一般软件在win下安装都是没什么问题的，但是我在安装OpenModelica的时候，第一次，先是下载了最新版本，（没有选择以管理员身份运行）自定义安装目录，安装快完成的时候提示安装失败。第二次，以为最新版不稳定，重新下载了OpenModelica-v1.11.0-64bit.exe这个版本，同样没有以管理员身份运行，选择了自定义安装目录，依然失败告终；第三次，用OpenModelica-v1.11.0-64bit.exe这个版本选择了管理员身份运行，默认的安装目录（C盘），最后安装成功了，问题不知道出在了哪里，因为有两个影响因素，本人就不折腾了，有兴趣的同学可以分别试一下。

程序运行

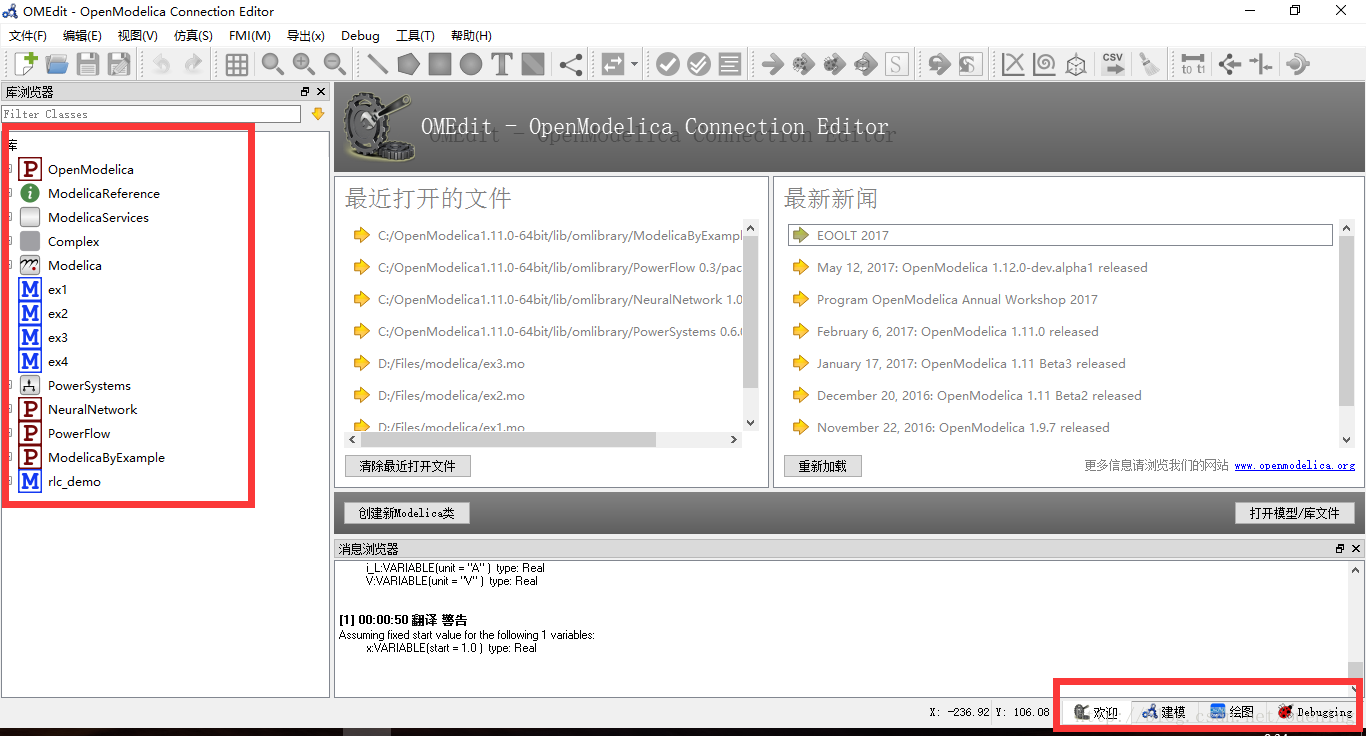
安装完之后，在所有程序那里会找到几个程序，打开OpenModelica Connection Editor，最后如下图，注意红色方框的地方，左边是各种库文件，默认的只有上面几个，下面几个要自己添加进去，右下角是界面切换的按钮，编译之后会出现绘图界面，返回到模型界面需要那里转换

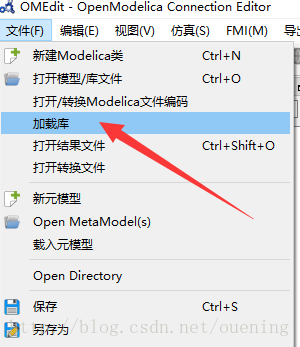
添加库

OpenModelica安装之后会有很多库了，位于"C:\OpenModelica1.11.0-64bit\lib\omlibrary"，

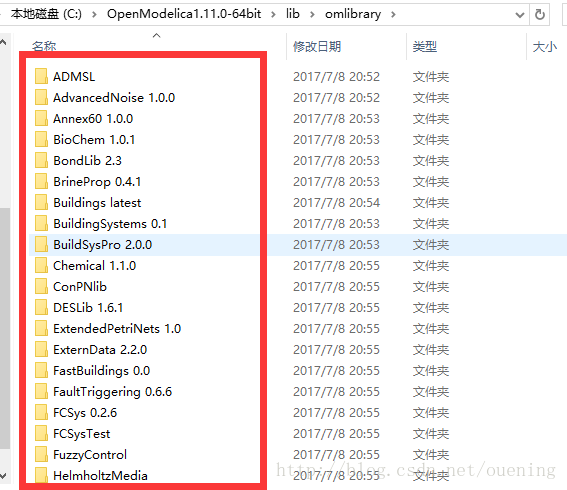
具体安装如下图

建立模型

下面仿真两种RLC电路，新建一个Model，如图，
（1）代码1

model rlc_demo "A resistor-inductor-capacitor circuit model"
  type Voltage=Real(unit="V");
  type Current=Real(unit="A");
  type Resistance=Real(unit="Ohm");
  type Capacitance=Real(unit="F");
  type Inductance=Real(unit="H");
  parameter Voltage Vb=24 "Battery voltage";    // 电源电压24V
  parameter Inductance L = 1;
  parameter Resistance R = 100;
  parameter Capacitance C = 1e-3;

  Voltage V_R;
  Voltage V_L;
  Voltage V_C;

  Current i;

// RLC 二阶电路
equation

  C*der(V_C) = i;     // 电容通过的电流
  V_R = i * R;
  V_L = L * der(i);   // 电感上的电压
  Vb = V_R + V_C + V_L;


end rlc_demo;

（2）代码2

model RLC1 "A resistor-inductor-capacitor circuit model"
  type Voltage=Real(unit="V");
  type Current=Real(unit="A");
  type Resistance=Real(unit="Ohm");
  type Capacitance=Real(unit="F");
  type Inductance=Real(unit="H");
  parameter Voltage Vb=24 "Battery voltage";
  parameter Inductance L = 1;
  parameter Resistance R = 100;
  parameter Capacitance C = 1e-3;
  Voltage V;
  Current i_L;
  Current i_R;
  Current i_C;
equation
  V = i_R*R;
  C*der(V) = i_C;       // 流进电容的电流公式
  L*der(i_L) = (Vb-V);  // 电感上的电压
  i_L=i_R+i_C;          // 基尔霍夫电流定律
end RLC1;

模型中的变量名和方程数要保持一致，不然会报错.

der(V)是对时间的求导(derivative)，这点和一般的求微分方程不同，der(var)都是变量var对时间的求导，由下面的绘图结果也可以知道横坐标为时间time，即der(x)看作是

$$der(x)=>\frac{dx}{dt}$$

模型编译及绘图

（1）编译

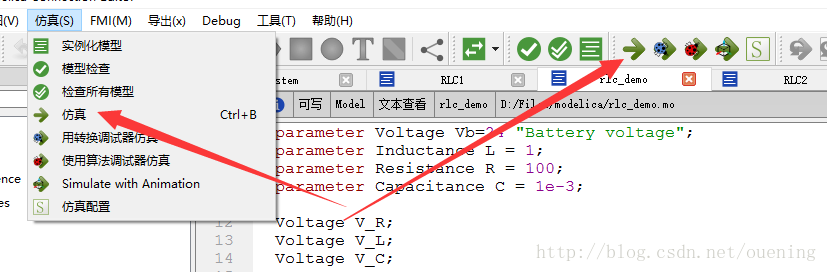
点击仿真运行，运行后会出现一个界面显示编译状态

（2）绘图
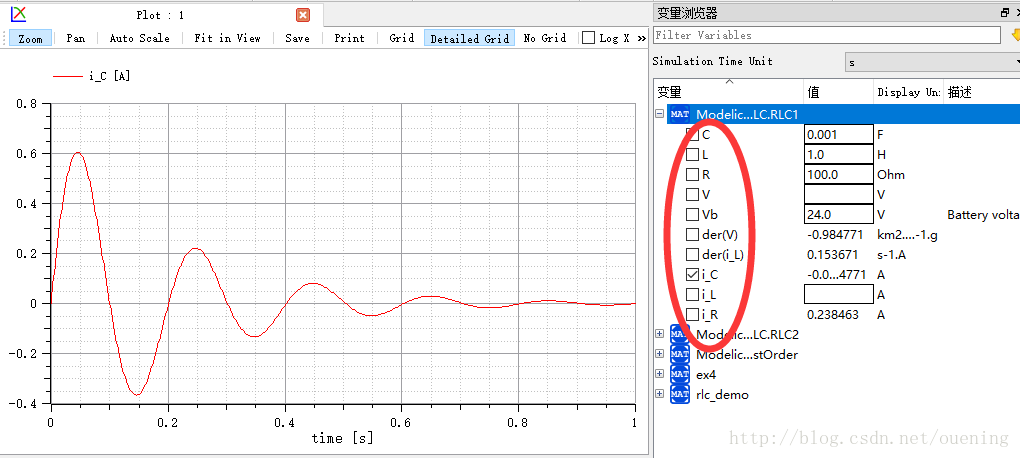
1) RLC1

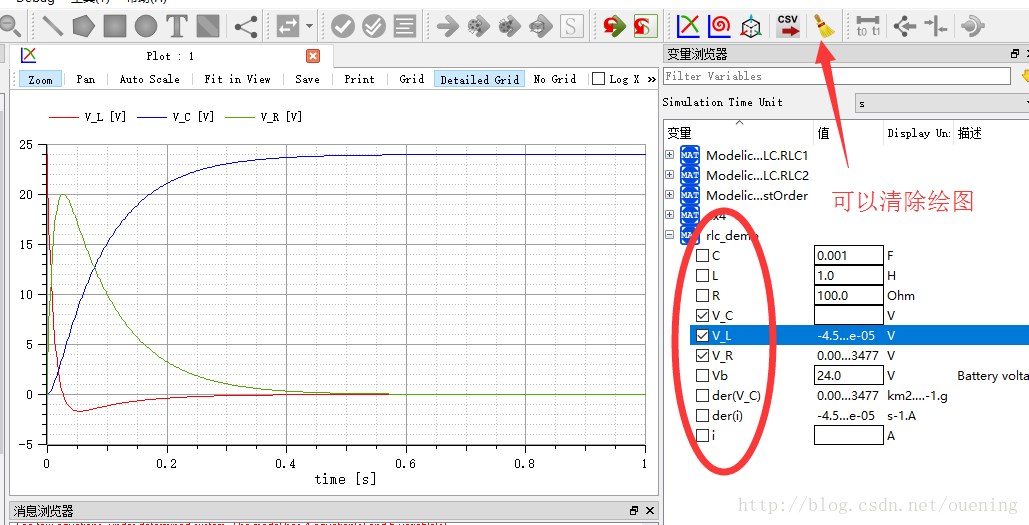
2) RLC2

暂时写到这里，后续补充