grbl控制3轴机械臂原理实现（二）之3D机械臂模拟及实现

最新推荐文章于 2024-10-10 08:16:11 发布

ourkix

最新推荐文章于 2024-10-10 08:16:11 发布

阅读量8.1k

点赞数 14

分类专栏：硬件文章标签： 3D机械臂运动学逆解 Unity模拟 GRBL控制步进电机

本文链接：https://blog.csdn.net/ourkix/article/details/113973066

版权

硬件专栏收录该内容

13 篇文章

订阅专栏

参考文章:https://www.alanzucconi.com/2020/09/14/inverse-kinematics-in-3d/

上一篇:grbl控制3轴机械臂原理实现（一）之2D机械臂模拟及实现

3轴机械臂几何分析

到目前为止，我们知道了如何在XY平面约束的情况下解决正逆运动学问题。从2D到3D的诀窍是重新使用2D解决方案。我们所介绍的这种3轴机械臂，一共3个轴，控制L1臂一个轴，控制L2臂一个轴，底座将L1和L2臂整体旋转为一个轴。很明显我们就多了一个整体旋转的维度。并且底座的旋转不会改变L1和L2臂的角度。

我们可以通过三个步骤解决问题：

绕Y轴旋转目标点，直到它位于XY平面上
移动机械臂L1和L2臂，使其到达目标该点，就像在2D模式下一样
通过沿Y轴的相反方向旋转整个机械臂来“撤消”旋转。

以上三个步骤逆解举例：

假设我们最终要得到的目标点是下图红色点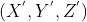 $(X^{'} ,Y^{'} , Z^{'} )$ ，那么我们就要求得大臂旋转角度，小臂旋转角度，两臂在Y轴旋转角度

根据步骤一，绕Y轴旋转到X，Y平面上如下图，这样我们就能像处理2D机械臂一样

步骤二，在此平面上处理得到的L1，L2臂角度

步骤三，得到L1，L2臂的角度后，恢复Y轴的旋转，并求得Y轴的旋转角度

根据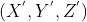 $(X^{'} ,Y^{'} , Z^{'} )$ 的值，求得紫色的线与X轴的夹角，这个夹角就是Y轴的旋转角度

至此，3个角度都求出来了。

实际上，旋转Y轴是为了方便理解，实际应用中，我们可以认为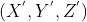 $(X^{'} ,Y^{'} , Z^{'} )$ 目标点所处于平面(W,Y)上

在这个(W,Y)平面上，直接按2D机械臂方式来算出L1，L2臂的角度即可，Y轴旋转角度计算照旧。

3D运动学逆解（Inverse kinematics）

我们把2d机械臂的图画到3d里面，可见原来我们的X边，变成了W边

根据坐标轴得知W边在（X，Z）平面，根据X边，W边，Z边是直角三角形，通过公式 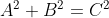A^2 + B^2 = C^2 求出W的长度

代入值得

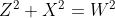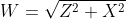
Z^2 + X^2 = W^2 得 $W = \sqrt{Z^2 + X^2}$

再根据W边和Y边求出原点到（X,Y,Z）的距离为A边，W边，Y边，A边是直角三角形，依旧通过公式 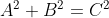A^2 + B^2 = C^2

代入值得

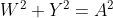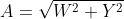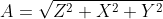
W^2 + Y^2 = A^2 得 $A = \sqrt{W^2 + Y^2}$ 代入上面W得 $A = \sqrt{Z^2 + X^2 + Y^2}$

接下来就和2d机械臂一样了

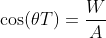$\cos(\theta T) = \frac{W}{A}$ 代入以上公式得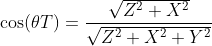 $\cos(\theta T) = \frac{\sqrt{Z^2 + X^2}}{\sqrt{Z^2 + X^2 + Y^2}}$

得

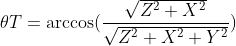
$\theta T = \arccos(\frac{\sqrt{Z^2 + X^2}}{\sqrt{Z^2 + X^2 + Y^2}})$

余弦定理公式：

$A^2 = B^2 + C^2 - 2BC\cos(\alpha )$

根据余弦定理，将值代入公式得

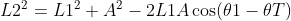
$L2^2 = L1^2 + A^2 - 2L1A\cos(\theta 1-\theta T)$

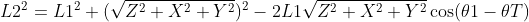
$L2^2 = L1^2 + (\sqrt{Z^2 + X^2 + Y^2})^2 - 2L1\sqrt{Z^2 + X^2 + Y^2}\cos(\theta 1-\theta T)$

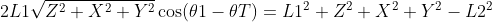
$2L1\sqrt{Z^2 + X^2 + Y^2} \cos(\theta 1 - \theta T) = L1^2 + Z^2 + X^2 + Y^2 - L2^2$

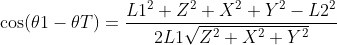
$\cos (\theta1 - \theta T) = \frac{L1^2 + Z^2 + X^2 + Y^2 - L2^2}{2L1 \sqrt{Z^2 + X^2 + Y^2}}$

$\theta1 = \arccos( \frac{L1^2 + Z^2 + X^2 + Y^2 - L2^2}{2L1 \sqrt{Z^2 + X^2 + Y^2}}) + \theta T$

同上根据余弦定理：

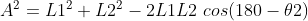
$A^2 = L1^2 +L2^2 - 2L1L2 \ cos(180-\theta 2)$

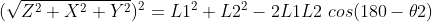
$(\sqrt{Z^2+X^2+Y^2})^2 = L1^2 +L2^2 - 2L1L2 \ cos(180-\theta 2)$

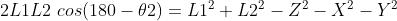
$2L1L2 \ cos(180-\theta 2) = L1^2 +L2^2 - Z^2-X^2-Y^2$

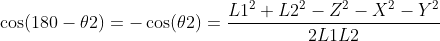
$\cos(180 - \theta2) = - \cos(\theta2) = \frac{L1^2 + L2^2 - Z^2 - X^2 - Y^2}{2L1L2}$

有：

$\theta2 = \arccos(\frac{Z^2 + X^2 + Y^2 - L1^2 - L2^2}{2L1L2})$

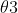$\theta 3$ 是X轴到W边的角度，我们用三角函数来求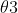 $\theta 3$

Z边，X边，W边组成一个直角三角形，则

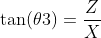$\tan(\theta 3) = \frac{Z}{X}$ 得 $\theta 3 = \arctan(\frac{Z}{X})$

这就求出3D机械臂的三个旋转角度了。

3D运动学正解（Forward kinematics）

对于3D机械臂的运动学正解，依旧可以和2D机械臂的方法。

首先我们已知L1，L2臂的臂长，L1，L2臂的角度和机械臂在Y轴旋转的角度，求坐标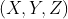 (X,Y,Z)

首先和2D机械臂一样，我们先求X，Y的坐标，在这里就是W，Y平面，就是求W和Y的值。

w1,w2,y1,y2分别是浅蓝色线段部分

由于w1和w2是平行的，所以L1和w1所成角度，和L1和w2所成角度相同，所以有

$\theta3 = 90 - \theta1$

根据三角函数:

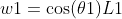
$w1 = \cos(\theta 1) L1$

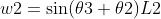
$w2 = \sin(\theta3 + \theta2)L2$

$y1 = \sin(\theta1)L1$

$y2 = \cos(\theta3 + \theta2)L2$

则

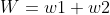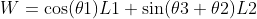
W =w1 + w2 代入上式得 $W = \cos(\theta 1) L1 + \sin(\theta3 + \theta2)L2$

Y = y1 + y2 代入上式得 $Y = \sin(\theta1)L1 + \cos(\theta3 + \theta2)L2$

然后根据W的值，求X和Z的值

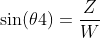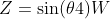
$\sin(\theta 4) = \frac{Z}{W}$ 得 $Z = \sin(\theta 4 ) W$

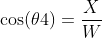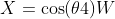
$\cos(\theta 4) = \frac{X}{W}$ 得 $X = \cos(\theta 4 ) W$

至此求得X，Y，Z的值

软件模拟实现

这里用的unity进行的模拟，通过unity里面的父子组件关系，L1旋转可以带动其子组件L2一起旋转。所以一个臂是由两部分组成的joint和arm如图

这样把两个臂组装起来，再把他们绑在一个原点方块this上

它们的父子关系是

this
- joint0
  - arm0
  - joint1
    - arm1

组合好后的样子

此脚本放在this方块上，并把joint0，joint1,的transform拖到脚本的公共变量上

代码实现：

using System.Collections;
using System.Collections.Generic;
using UnityEngine;



public class ik : MonoBehaviour {




    //[Header("Joints")]
    public Transform Joint0;
    public Transform Joint1;
    public Transform Hand;

    //[Header("Target")]
    public Transform Target;


    private float length0, L1;
    private float length1, L2;

    private float L1_2, L2_2;

    private int X_AXIS = 0;
    private int Y_AXIS = 1;
    private int Z_AXIS = 2;

    private float SCARA_OFFSET_X = 0;
    private float SCARA_OFFSET_Y = 0.72f;
    private float SCARA_OFFSET_Z = 0;

    public bool angle_mode = false;

    private float[] cartesian = new float[3], f_scara = new float[3];


    void Start()
    {
        length0 = Vector3.Distance(Joint0.position, Joint1.position);
        length1 = Vector3.Distance(Joint1.position, Hand.position);
        L1 = length0;
        L2 = length1;
        L1_2 = sq(L1);
        L2_2 = sq(L2);


    }




    // Update is called once per frame
    void Update() {






        float length2 = Vector3.Distance(Joint0.position, Target.position);

        if (length2 > length0 + length1 - 0.3f)
        {

        }
        else
        {
            cartesian[0] = Target.position.x;
            cartesian[1] = Target.position.y;
            cartesian[2] = Target.position.z;

            inverse_kinematics(cartesian, f_scara);

            float[] cart = new float[3];
            float[] scar = new float[3];

            scar = (float [])f_scara.Clone();

            forward_kinematics_SCARA(scar, cart);
            Debug.Log("x:" + cart[0]);
            Debug.Log("y:" + cart[1]);
            Debug.Log("z:" + cart[2]);
        }

        Joint0.transform.localEulerAngles = new Vector3(0, 0, 0);
        Vector3 Euler0 = Joint0.transform.localEulerAngles;
        Euler0.x = 90f - f_scara[0];
        Joint0.transform.localEulerAngles = Euler0;

        Joint1.transform.localEulerAngles = new Vector3(0, 0, 0);
        Vector3 Euler1 = Joint1.transform.localEulerAngles;
        Euler1.x = f_scara[1];
        Joint1.transform.localEulerAngles = Euler1;

        this.transform.localEulerAngles = new Vector3(0, 0, 0);
        Vector3 Euler2 = this.transform.localEulerAngles;
        Euler2.y = f_scara[2];
        this.transform.localEulerAngles = Euler2;


    }


    float sq(float a)
    {
        return a * a;

    }


    // f_scara是大臂和小臂的角度，cartesian是坐标
    void inverse_kinematics(float[] cartesian, float[] f_scara)
    {
        /***********************robot arm****************************/

        //         y +  /z
        //           | /
        //           |/
        //           +-----+x

        float ROBOTARM_alpha, ROBOTARM_beta, ROBOTARM_cta, ROBOTARM_alphapsi, projectxyLength, X, Y, X_2, Y_2, sqrtx_2ay_2;

        //首先求得目标点 到 原点的距离
        //获取机械臂投射到xy平面的长度
        //length = sqrt(x*x + y*y)
        projectxyLength = Mathf.Sqrt(sq(cartesian[X_AXIS]) + sq(cartesian[Z_AXIS]));//对调yz,坐标系不同
                                                                                    //将3d机械臂变量变为2d机械臂的变量
                                                                                    //	projectxyLength长度为2d机械臂的X
        X = projectxyLength;
        X_2 = sq(X);
        Y = cartesian[Y_AXIS];//对调yz,坐标系不同
        Y_2 = sq(Y);
        sqrtx_2ay_2 = Mathf.Sqrt(X_2 + Y_2);
        //求得机械臂所在yz旋转平面的alphapsi角度
        ROBOTARM_alphapsi = Mathf.Acos(X / sqrtx_2ay_2);
        //如果坐标在平面以下，将alphapsi取反
        if (Y < 0)
        {
            ROBOTARM_alphapsi = -ROBOTARM_alphapsi;
        }

        //求得机械臂所在yz旋转平面的alpha角度,，即大臂到xy平面的角度(实际是弧度)
        ROBOTARM_alpha = Mathf.Acos((L1_2 + X_2 + Y_2 - L2_2) / (2 * L1 * sqrtx_2ay_2)) + ROBOTARM_alphapsi;
        //求得小臂的角度(实际是弧度)
        ROBOTARM_beta = Mathf.Acos((X_2 + Y_2 - L1_2 - L2_2) / (2 * L1 * L2));
        //求得整体机械臂的旋转角度(实际是弧度)
        ROBOTARM_cta = Mathf.Atan2(cartesian[X_AXIS], cartesian[Z_AXIS]);

        //如果不是角度模式
        if (!angle_mode)
        {
            f_scara[X_AXIS] = Mathf.Rad2Deg * ROBOTARM_alpha; //大臂旋转弧度转换为角度
            f_scara[Y_AXIS] = Mathf.Rad2Deg * ROBOTARM_beta;   //小臂旋转弧度转换为角度
            f_scara[Z_AXIS] = Mathf.Rad2Deg * ROBOTARM_cta;
        }
        //否则是角度模式
        else
        {
            f_scara[X_AXIS] = cartesian[X_AXIS];
            f_scara[Y_AXIS] = cartesian[Y_AXIS];
            f_scara[Z_AXIS] = cartesian[Z_AXIS];

        }
    }



    //传入值 f_scara是大臂和小臂的角度，cartesian是最终求得的坐标
    void forward_kinematics_SCARA(float [] f_scara, float [] cartesian)
    {
        /***********************robot arm****************************/
        float X, Y, Z;
        float project3D;
        //f_scara里面的0,1,2代表：大臂角度，小臂角度，旋转角度


        //         y +  /z
        //           | /
        //           |/
        //           +-----+x


        //unity 角度空间转换转换
        //f_scara[X_AXIS] = 90f - f_scara[X_AXIS];

        //2D机械臂朝向的方向,两臂投影到平台平面长度
        //Z = Mathf.Cos(Mathf.Deg2Rad * f_scara[X_AXIS]) * L1 + Mathf.Sin((Mathf.Deg2Rad * f_scara[Y_AXIS]) + (Mathf.Deg2Rad * 90) - (Mathf.Deg2Rad * f_scara[X_AXIS])) * L2;

        //3D 两臂投影到平台平面长度,通过三角函数转化为坐标轴方向长度
        project3D =  Mathf.Cos(Mathf.Deg2Rad * f_scara[X_AXIS]) * L1 + Mathf.Sin((Mathf.Deg2Rad * f_scara[Y_AXIS]) + (Mathf.Deg2Rad * 90) - (Mathf.Deg2Rad * f_scara[X_AXIS])) * L2;
        Z = Mathf.Cos((Mathf.Deg2Rad * f_scara[Z_AXIS])) * project3D;

        //垂直向上的方向
        Y = Mathf.Sin((Mathf.Deg2Rad * f_scara[X_AXIS])) * L1 + Mathf.Cos((Mathf.Deg2Rad * f_scara[Y_AXIS]) + (Mathf.Deg2Rad * 90) - (Mathf.Deg2Rad * f_scara[X_AXIS])) * L2;

        //2D 站机械臂后方看向它，它的右边方向
        //X = Mathf.Sin((Mathf.Deg2Rad * f_scara[Z_AXIS])) * Mathf.Cos((Mathf.Deg2Rad * f_scara[X_AXIS])) * L1 + Mathf.Sin((Mathf.Deg2Rad * f_scara[Y_AXIS]) + (Mathf.Deg2Rad * 90) - (Mathf.Deg2Rad * f_scara[X_AXIS])) * L2;

        //3D 站机械臂后方看向它，它的右边方向
        X = Mathf.Sin((Mathf.Deg2Rad * f_scara[Z_AXIS])) * project3D;




        cartesian[X_AXIS] = X + SCARA_OFFSET_X;  //求得机械手顶点的坐标
        cartesian[Y_AXIS] = Y + SCARA_OFFSET_Y;  //求得机械手顶点的坐标
        cartesian[Z_AXIS] = Z + SCARA_OFFSET_Z;		
		
    /***********************robot arm****************************/	
    }


}

实现效果演示