脉冲函数（也称冲激函数）

听海边涛声

已于 2024-01-30 11:35:51 修改

阅读量1.7k

点赞数 6

文章标签：控制系统

于 2023-12-27 15:15:39 首次发布

本文链接：https://blog.csdn.net/panghuangang/article/details/135246363

版权

用矩形脉冲的极限来定义冲激函数

下图所示为宽为 $\tau$ ，高为 $\frac{1}{\tau }$ 的矩形脉冲，当保持矩形面积 $\tau \cdot \frac{1}{\tau }=1$ 不变，而使脉冲宽度 $\tau$ 趋向于零时，脉冲幅度 $\frac{1}{\tau }$ 趋向于无穷大，这种极限情况就是单位冲激函数，一般用用符号 $\delta (t)$ 表示，又称做 $\delta$ 函数。

$\delta (t)=\lim_{\tau \to 0}\frac{1}{\tau }\left [ u(t+\frac{\tau }{2})-u(t-\frac{\tau }{2}) \right ]\; \; \; \; (1-1)$

上面公式中， $u(t)$ 表示单位阶跃函数， $\frac{1}{\tau }\left [ u(t+\frac{\tau }{2})-u(t-\frac{\tau }{2}) \right ]$ 是由两个阶跃函数合成的脉动函数。也就是说，脉动函数的极限就是脉冲函数。它的宽度趋向于0，高度趋向于无穷大，面积等于1。

单位冲激函数示意图用箭头表示，如下图所示

它示意表明， $\delta (t)$ 只在 $t=0$ 点有一“冲激”，在 $t=0$ 以外各处，函数值都是零。

在 $t_{0}$ 时刻出现的单位脉冲函数表示为 $\delta (t-t_{0})$ 。

脉冲函数的强度一般用面积来表示。强度为 $E$ 的脉冲函数 $f(t)$ 可以表示为 $f(t)=E\delta (t)$ 。在 $t_{0}$ 时刻出现的脉冲函数表示为 $f(t-t_{0})=E\delta (t-t_{0})$ 。

狄拉克（Dirac）给出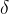 $\delta$ 函数另外一种定义方式

$\left\{\begin{matrix} \int_{-\infty }^{\infty }\delta (t)dt=1\\ \delta (t)=0\; \; \; \; \; \; (t\neq 0) \end{matrix}\right.\; \; \; \; (2-1)$

此定义与(1-1)式的定义相符合。有时，也称 $\delta$ 函数为狄拉克函数。

为了描述在任何一点 $t=t_{0}$ 处出现的冲激，用如下的 $\delta (t-t_{0})$ 的定义

$\left\{\begin{matrix} \int_{-\infty }^{\infty }\delta (t-t_{0})dt=1\\ \delta (t-t_{0})=0\; \; \; \; \; \; (t\neq t_{0}) \end{matrix}\right.\; \; \; \; (2-1)$

示意图

冲激函数的性质

抽样特性（或称筛选特性）

如果单位冲激信号 $\delta (t)$ 与一个在 $t=0$ 处连续、且处处有界的信号 $f(t)$ 相乘，则其乘积仅在 $t=0$ 处得到 $f(0)\delta (t)$ ，其余各点之乘积均为零，因此得到冲激函数的如下性质

$\int_{-\infty }^{\infty }\delta (t)f(t)dt=\int_{-\infty }^{\infty }\delta (t)f(0)dt$

$=f(0)\int_{-\infty }^{\infty }\delta (t)dt=f(0)\; \; \; \; \; (3-1)$

同理，对于延迟 $t_{0}$ 的单位冲激信号，有

$\int_{-\infty }^{\infty }\delta (t-t_{0})f(t)dt=\int_{-\infty }^{\infty }\delta (t-t_{0})f(t_{0})dt=f(t_{0})\; \; \; \; (3-2)$

从上面两个公式可以看出冲激信号的抽样特性（或称筛选特性）：连续信号 $f(t)$ 与单位冲激信号 $\delta (t)$ 相乘，并在 $-\infty$ 到 $\infty$ 范围内取积分，可以得到 $f(t)$ 在 $t=0$ 时刻的抽样值 $f(0)$ ；若将单位冲激响应移到 $t_{0}$ 时刻，则筛选出 $f(t_{0})$ 。