【复变函数与积分变换】第8章 拉普拉斯变换的定义，性质，相关定理，各种函数的拉普拉斯变换（武汉大学）

目录

§8.1   拉普拉斯变换定义

阶跃函数的拉普拉斯变换​编辑

​编辑

指数函数的拉普拉斯变换​编辑

幂函数的拉普拉斯变换​编辑​编辑

定理8.1​编辑

正弦函数的拉普拉斯变换

单位脉冲函数的拉普拉斯变换

§8.2  拉普拉斯变换的性质

求正弦函数的拉普拉斯变换

​编辑​编辑求阶跃函数和延迟函数的拉普拉斯变换

​编辑

定理8.3 微分性质​编辑

求余弦函数的拉普拉斯变换

定理 8.4 积分性质

定理8.6 终值定理​编辑​编辑​编辑

卷积定理

§8.3 拉普拉斯逆变换

定理8.8

例8.19

例8.21

§8.4  拉普拉斯变换的应用

---

§8.1   拉普拉斯变换定义

阶跃函数的拉普拉斯变换

指数函数的拉普拉斯变换

幂函数的拉普拉斯变换

用分部积分法，得

定理8.1

分与微分的次序可以交换，于是有

由拉普拉斯变换的定义，得

正弦函数的拉普拉斯变换

例8.4 求正弦函数sinkt的拉普拉斯变换，其中k为实数.

余弦函数coskt的拉普拉斯变换

单位脉冲函数的拉普拉斯变换

§8.2  拉普拉斯变换的性质

证明： 性质1说明函数的线性组合的拉普拉斯变换等于各函数的拉普拉斯变换的线性组合.

证明性质2

求正弦函数的拉普拉斯变换

例8.8 求函数的拉普sinwt拉斯变换，其中w为实数.

求阶跃函数和延迟函数的拉普拉斯变换

解：阶跃函数u(t)的拉普拉斯变换为

根据延迟性质，有

定理8.3 微分性质

证明：由拉普拉斯变换的定义，有

由分部积分公式，得    

求余弦函数的拉普拉斯变换

定理 8.4 积分性质

定理8.6 终值定理

卷积定理

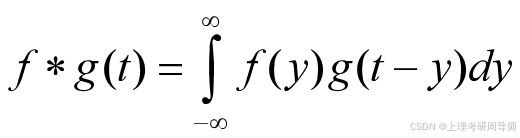
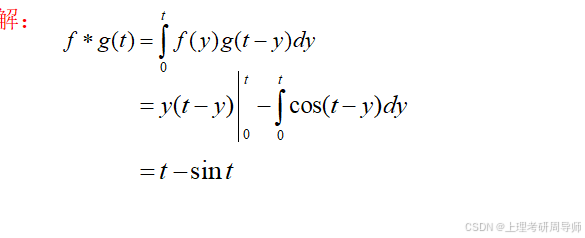
证明：容易得到满足拉普拉斯变换存在定理的条件，其变换式为

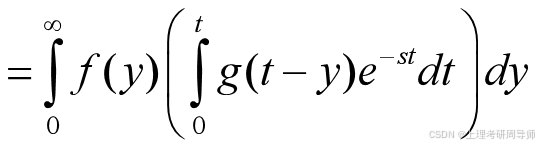
作变量替换，则有

故有

§8.3 拉普拉斯逆变换

从象函数F(s)出发求原象函数f(t)的一般公式. 右端的积分称为拉普拉斯变换的反演积分.

定理8.8

例8.19

例8.21

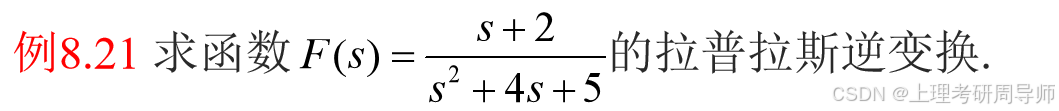
§8.4  拉普拉斯变换的应用

---

---

资料仅供学习使用

如有错误欢迎留言交流

上理考研周导师的其他专栏：

光电融合集成电路技术     电路原理

C语言       复变函数与积分变换

单片机原理

模式识别原理

数字电子技术

自动控制原理     ​​​​​​ 传感器技术

模拟电子技术

数据结构

 概率论与数理统计

高等数学

传感器检测技术

智能控制

嵌入式系统

图像处理与机器视觉

热工与工程流体力学

数字信号处理

线性代数

工程测试技术

上理考研周导师了解更多