控制系统的数学模型

控制系统的数学模型

一.数学模型的建立

在线性系统中，常用的数学模型有传递函数模型、零极点模型以及状态空间模型等

(1)传递函数模型

传递函数的一般形式

$$G(s)=\frac{C(s)}{R(s)}=\frac{b_0{s}^m+b_1{s}^{m-1}+\cdots +b_{m-1}s+b_m}{a_0{s}^n+a_1{s}^{n-1}+\cdots +a_{n-1}s+a_n}$$

函数调用格式

sys=tf(num,den);		

• tf–transfer function(传递函数模型)
• num–numerator(传递函数分子的多项式系数向量） 一定要降幂排列，缺项补零！
• den–denominator(传递函数分母的多项式系数向量）同上

实例

​ 请构建如下传递函数
$$G(s)=\frac{7s^2+8s+1}{9s^3+8s^2+3s+1}$$

num=[7 8 1];
den=[9 8 3 1];
sys=tf(num,den)

​ 拓展：(结合卷积函数conv构建多项式—适用于未展开且比较复杂的多项式)

​ 请构建如下传递函数
$$G(s)=\frac{(s+1)(7s+1)}{（3s+1)(2s+1)(7s+1)}$$

num=conv([1,1],[7,1]);
den=conv(conv([3 1],[2,1]),[7,1]);
sys=tf(num,den)

(2)零极点模型

零极点式一般形式

$$G(s)=\frac{C(s)}{R(s)}=K^{\ast }\frac{\left(s-z_1\right)\left(s-z_2\right)\cdots \left(s-z_j\right)\left(s-z_m\right)}{\left(s-p_1\right)\left(s-p_2\right)\cdots \left(s-p_i\right)\left(s-p_n\right)}$$

• z1,z2,…,zm为系统的m个零点，p1、p2、…pn为系统的n个极点，$K^{\ast }$称为根轨迹增益

• 零极点式等价于首一式，对应根轨迹增益；而相对应于尾一式(典型环节）,对应开环增益

  尾一式的数学表达如下
  $$G(s)=\frac{K\left({\tau }_{1}s+1\right)\left({\tau }_2^2{s}^2+2{\zeta }_1{\tau }_{2}s+1\right)\cdots \left({\tau }_{l}s+1\right)}{s^{\nu }\left(T_{1}s+1\right)\left(T_2^2{s}^2+2{\zeta }_2{T}_{2}s+1\right)\cdots \left(T_{j}s+1\right)}$$
  其中K为开环增益，v为系统型别

函数调用格式

sys=zpk(z,p,k);

• z（zero）–由零点构成的向量
• p（polar）–由极点构成的向量
• k–根轨迹增益

实例

​ 请构造如下传递函数
$$G(s)=\frac{20(s+1)(s+2)}{(s+4)(s+5)(s+6)}$$

z=[-1 -2];
p=[-4 -5 -6];
k=20;
sys=zpk(z,p,k)

二.数学模型的转换

零极点形式和传递函数一般形式之间可以相互转换

（1）零极点到传递函数

函数调用格式

[num,den]=zp2tf(z,p,k);

• 一定注意函数名不是 zpk2tf ！！！

实例

​ 将如下零极点格式模型转化为传递函数标准形式
$$G(s)=\frac{20(s+1)(s+2)}{(s+4)(s+5)(s+6)}$$

z=[-1;-2];  %此处的z一定是一个列向量。感觉以后也记不住，可以记忆个大概结合报错来修改自己的程序
p=[-4 -5 -6];
k=20;
[num,den]=zp2tf(z,p,k)

（2）传递函数到零极点

函数调用格式

[z,p,k]=tf2zp(num,den);

• 一定注意函数名不是 tf2zpk ！！！

实例

​ 将如下传递函数标准形式转化为零极点格式模型
$$G(s)=\frac{20s^2+60s+40}{s^3+15s^2+74s+120}$$

num=[20 60 40];
den=[1 15 74 120];
[z,p,k]=tf2zp(num,den);

运行之后就会发现（1）和（2）的实例中的模型是一致的

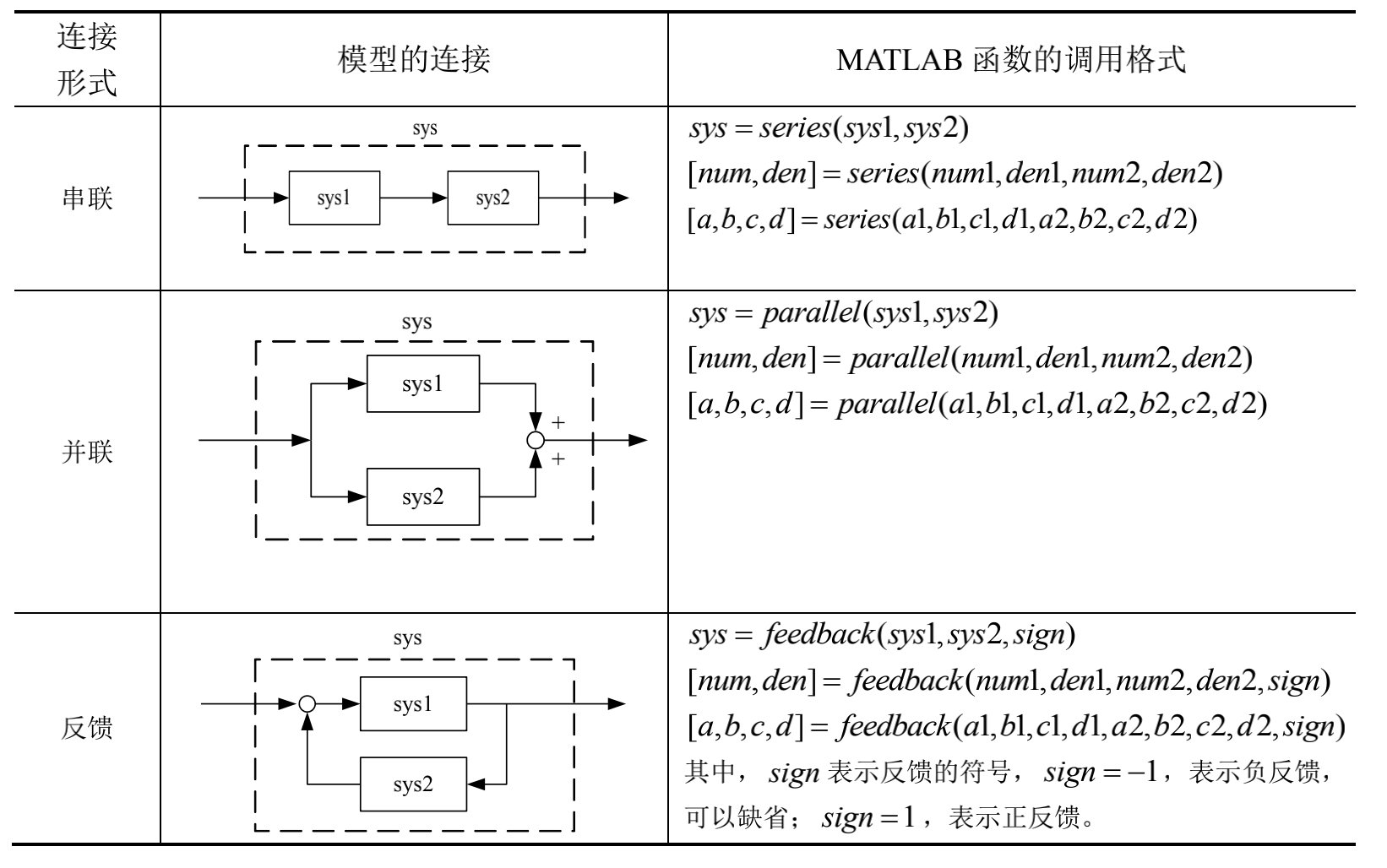
三.数学模型的连接

数学模型经过连接便可以构成控制系统的结构图，如何用matlab实现语句的连接便显得格外重要

按照连接方式，可以分为如下几类