http://blog.csdn.net/pipisorry/article/details/43966361
机器学习Machine Learning - Andrew NG courses学习笔记
规格化Regularization
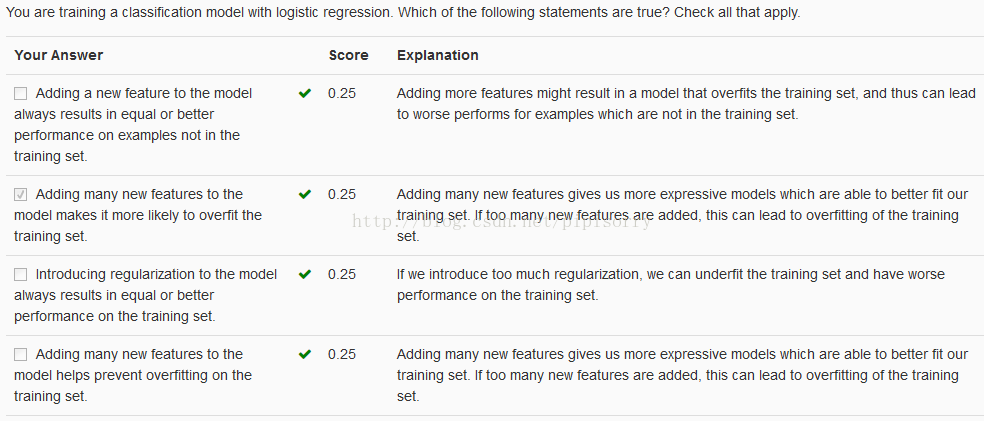
过拟合Overfitting
线性规划的例子(housing prices) 逻辑回归的例子(breast tumor cancer)
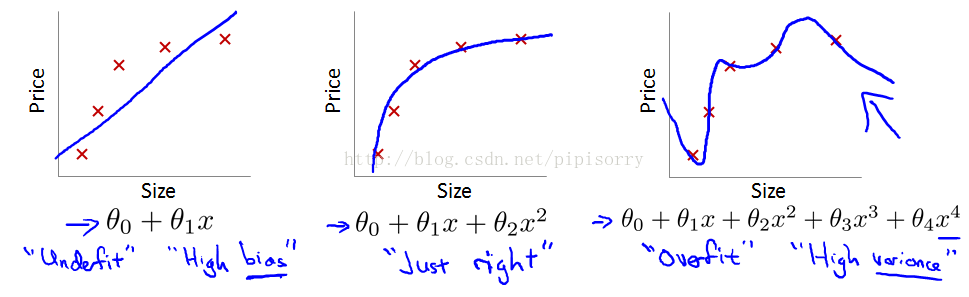
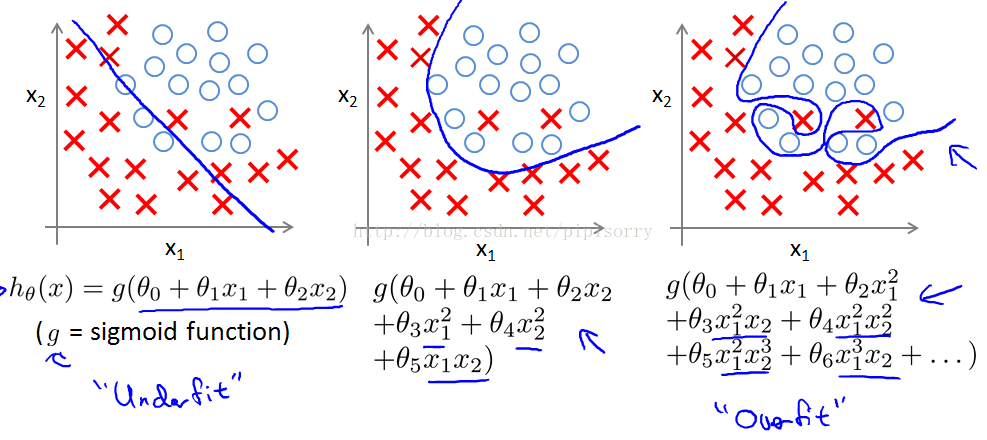
从左到右分别是欠拟合(underfitting,也称High-bias)、合适的拟合和过拟合(overfitting,High variance)三种情况。
欠拟合underfit(or the hypothesis having high bias; figure1): if the algorithm has a very strong preconception, or a very strong bias that housing prices are going to vary linearly with their size and despite the data to the contrary.
过拟合overfit(figure3): 可以看到,如果模型复杂(可以拟合任意的复杂函数),它可以让我们的模型拟合所有的数据点,也就是基本上没有误差。对于回归来说,就是我们的函数曲线通过了所有的数据点。对分类来说,就是我们的函数曲线要把所有的数据点都分类正确。这两种情况很明显过拟合了。The term high variance is a historical or technical one.But, the intuition is that,if we're fitting such a high order polynomial, then, the hypothesis can fit almost any function and this face of possible hypothesis is just too large, it's too variable.
And we don't have enough data to constrain it to give us a good hypothesis so that's called overfitting. the curve tries too hard to fit the training set, so that it even fails to generalize to new examples and fails to predict prices on new examples.
如在逻辑规划中,如果你有太多的features(不一定是多项式features),就可能导致过拟合。More generally if you have logistic regression with a lot of features.Not necessarily polynomial ones, but just with a lot of features you can end up with overfitting.
过拟合的存在也导致训练集误差并不是一个分类器在新数据上好坏评估的好指示器。
解决过拟合问题的方法
当我们有很多features,但是只有很少的训练数据时,就会有overfitting问题。而由于features太多又不好绘制,不好确定保留哪些features。
解决方法
怎么检测underfit & overfit?
鉴别两种类型的问题使用Learning Curves学习曲线方法来检测。
具体解决方法及检测具体的方法请参考[Machine Learning - X. Advice for Applying Machine Learning机器学习应用上的建议 (Week 6) ]
规格化:代价函数Cost Function
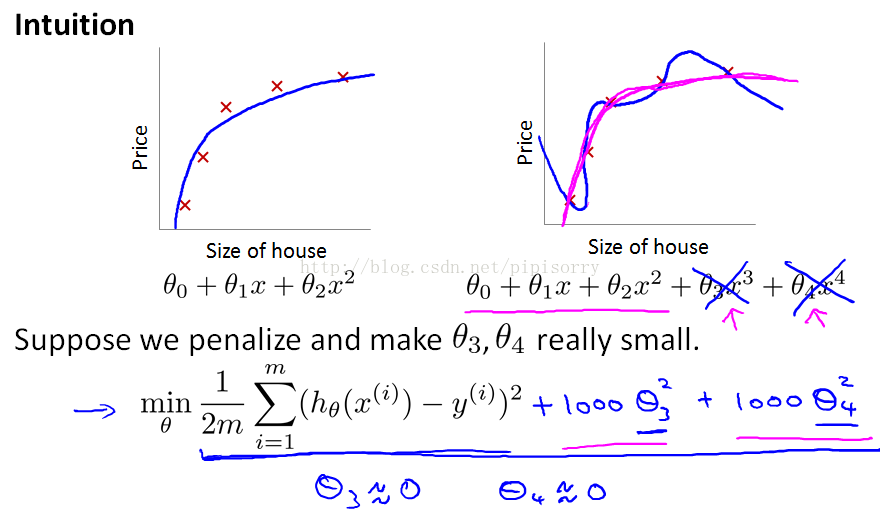
规格化的好处的Intuition
小的参数通过会导致smoother和simpler的函数。And it is kind of hard to explain unless you implement yourself and see it for yourself.
至于规格化有这么些好的特性的理论解释请参考我的另一篇博文[最优化方法:范数和规则化regularization ]。
规格化:在代价函数中惩罚参数
添加规格化项regularization term。Note: 包不包括0在实践中对结果影响不大。
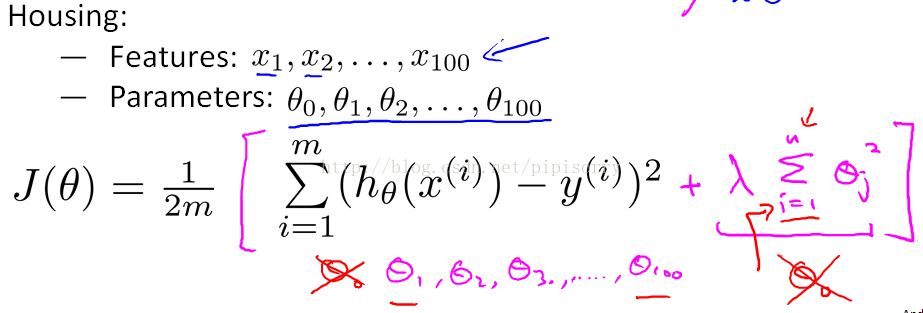
规格参数regularization parameter: λ
用于控制很好地拟合训练集和保持参数足够小的权衡,这样的话可以使hypothesis更简单从而避免过拟合。controls the trade of between the goal of fitting the training set well and the goal of keeping the parameter plan small and therefore keeping the hypothesis relatively simple to avoid overfitting.
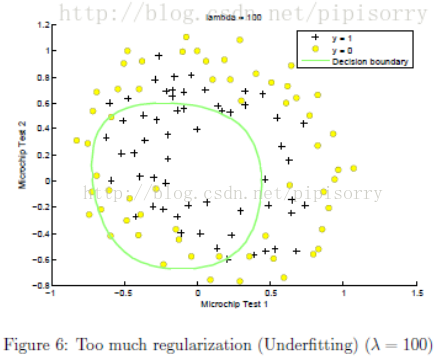
λ设置太大带来的问题
λ太大,惩罚参数太狠,所有参数都接近0,这样就可能拟合出一条水平线,导致欠拟合underfitting。
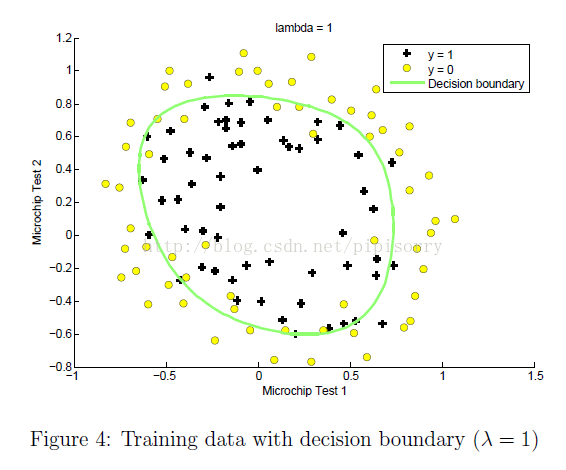
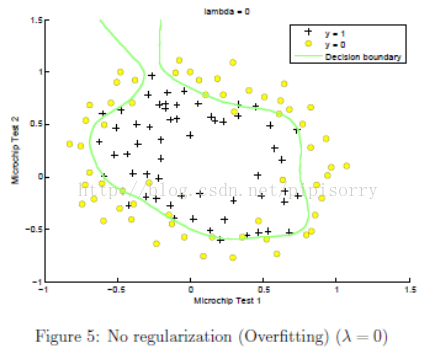
λ设置的影响:在mlclass-ex2 - 2.5 Optional (ungraded) exercises中的一个例子
参数λ怎么选择?
枚举λ,在交叉验证集上选择使误差最小的规格化参数。
参考[Machine Learning - X. Advice for Applying Machine Learning机器学习应用上的建议 (Week 6) ],同时分析了λ在训练集和交叉验证集上的bias和var的变化。
规格化线性规划Regularized Linear Regression
For linear regression, we had worked out two learning algorithms,gradient descent and the normal equation.There we take those two algorithms and generalize them to the case of regularized linear regression.
梯度下降解线性规划的改进
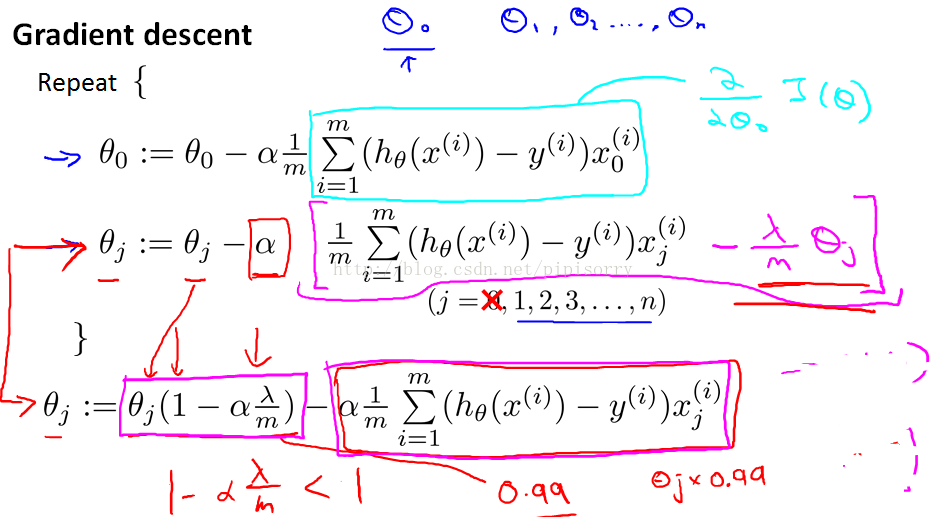
规格化线性回归时,我们并不惩罚θ0。
regularized的解释:在每一步规格化时,θJ总是乘上一个小于1的数,这样就可以shrinking参数θJ一点点,这也就是的效果。
Note: lz想,这样的话,是不是在很多问题中,我们只要用相当的思路,也就是在每次更新参数θ时,都乘一个小于1一点点的数就可以当成规格化了?毕竟其中的λ也是不确定的数。
Normal equation解线性规划的改进

推导: using the new definition of J of θ, with the regularization objective.Then this new formula for θ is the one that will give you the global minimum of J of θ.
Note: so long as the regularization parameter is strictly greater than zero.It is actually possible to prove that this matrix X transpose X plus parameter time, this matrix will not be singular and that this matrix will be invertible.
Regularized Logistic Regression规格化逻辑规划
规格化Gradient descent方法
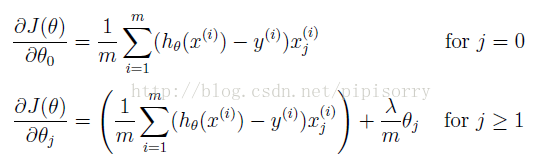
(注意:中括号里应该是+λ/m*θj)
规格化高级方法
Code for regularized logistic regression
1. code to compute the regularized cost function:
J = -1/m * (y' * log(sigmoid(X*theta)) + (1-y)' * log(1 - sigmoid(X*theta))) + lambda/(2*m) * (theta'*theta - theta(1)*theta(1));
2. code to compute the gradient of the regularized cost:
1> #vectorized,推荐
grad = 1/m*(X'*(sigmoid(X*theta)-y));
temp = theta;temp(1)=0;
grad = grad+lambda/m*temp;
2> #vectorized
tmp = X' * (sigmoid(X * theta) - y);
grad = (tmp + lambda * theta) / m;
grad(1) = tmp(1) / m;
3> #non-vectorized
grad(1) = 1/m*(sigmoid(X*theta)-y)'*X(:,1);for i=2:size(theta)
grad(i) = 1/m*(sigmoid(X*theta)-y)'*X(:,i) + lambda/m*theta(i);
end
Note: end keyword in indexing:One special keyword you can use in indexing is the end keyword in indexing.This allows us to select columns (or rows) until the end of the matrix.
For example, A(:, 2:end) will only return elements from the 2nd to last column of A. Thus, you could use this together with the sum and .^ operations to compute the sum of only the elements you are interested in(e.g., sum(z(2:end).^2)).
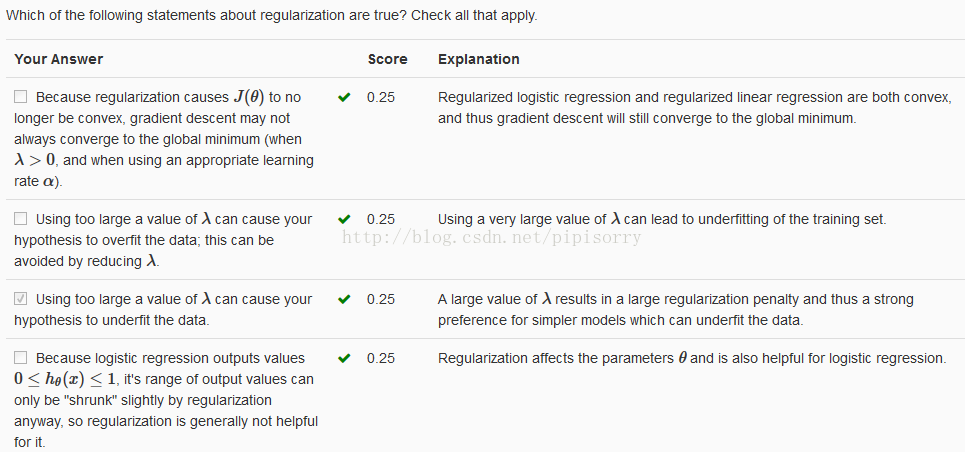
Review复习
from:http://blog.csdn.net/pipisorry/article/details/43966361










 本文深入探讨了机器学习中的规范化原理及其在不同场景的应用,包括逻辑回归、线性规划、欠拟合与过拟合的识别,以及如何通过调整参数避免过拟合。重点介绍了规范化在减少模型复杂度、提升泛化能力方面的关键作用,并提供了实用的规范化方法与案例分析。
本文深入探讨了机器学习中的规范化原理及其在不同场景的应用,包括逻辑回归、线性规划、欠拟合与过拟合的识别,以及如何通过调整参数避免过拟合。重点介绍了规范化在减少模型复杂度、提升泛化能力方面的关键作用,并提供了实用的规范化方法与案例分析。








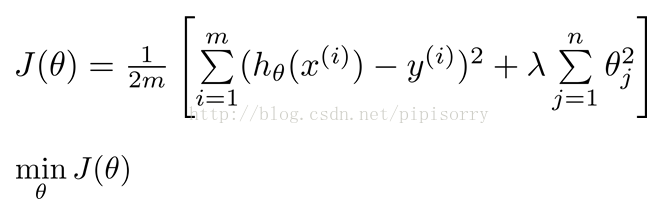


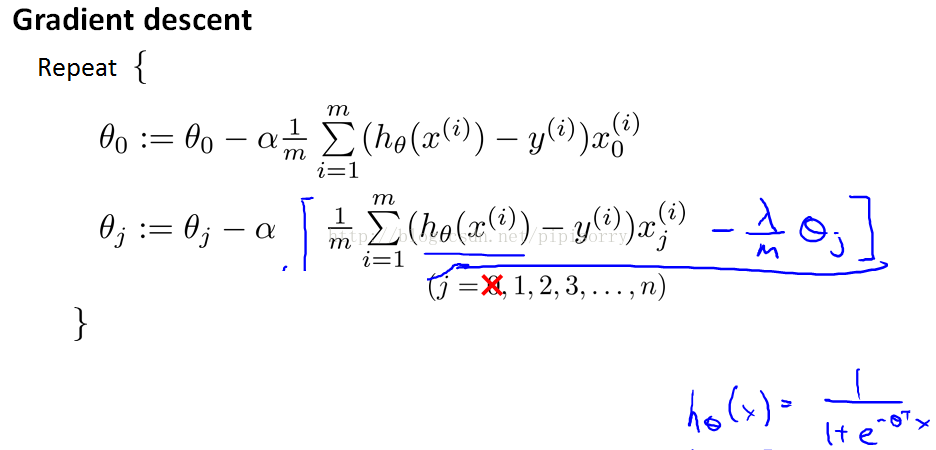


















 1534
1534

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








