机器学习知识总结 —— 14. 什么是支持向量机（基础概念、梯度下降、软间隔、硬间隔）？

什么是向量

如果从数学的定义出发，所谓「向量」指的是有向线段。但是如果我们从数据科学出发，向量通常指的是某样本的特征表述。举例来说，如果我们有如下一张表，记录了一个人的身高、体重等信息

姓名	性别	身高	体重
张三	男	168	65
李四	男	170	65

这种数据通常无法直接用计算机进行处理，所以对数据进行转换后，就可以变成

性别	身高	体重
1	168	65
1	170	65
0	160	56
0	163	54
1	175	74

然后随便从数据中抽一条样本出来，表示该样本的特征值所组成的集合（例如，【1，168，65】）就是一个所谓的向量（vector）。

如果数据选取妥当，我们把数据绘制到图上后，相关性比较高的数据（比如计算协方差 $cov(x)>0$ 或 $cov(x)<0$），样本会在图中聚集在一起。从经验可以知道，男性和女性除了少数个体外，大部分应该是男性的身高和体重均高于或重于女性，如果数据表中还有骨密度、体脂率等指标的话，那么这种预测一个样本是男性或是女性也就越准确。如果把这些数据绘制到表中，大致上应该可以看到相关性比较高的数据会聚集在一起，比如说一「坨」这样的概念。

如上图所示，我们的数据大致分为两「坨」，如果我们用黑色圆点表示样本为男性，白色圆点为女性。那么也许会想到是否可以给这两坨样本之间划分一个或数个区域，如果一个新的样本它的特征满足其中某一个区域的全部要求，就可以预测它是男性样本或是女性样本。

由于数据的划分方式有很多，例如上图中的H1，H2，H3，那么我们如何评价以上划分方式，哪种更科学呢？这样就提出了第二个问题，什么是「支持向量（Support-vectors）」

什么是支持向量

我们肯定希望能 $n-1$ 刀顺利的把数据分割成 $n$ 个不同的分类。 比分说对于我们这里提到的例子，有男性和女性两个类别。我们不能接受的是样本分类时，把本应该属于男性的样本分到了女性的样本集合里。

所以上图中H1，H2的分类方式是不可以接受的。那么对于H3来说，满足这种类似的分割方式又有很多，例如下图：

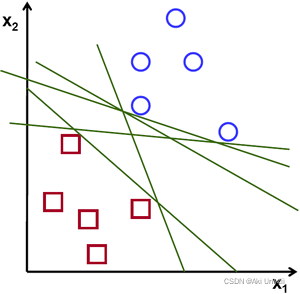
如何判断H3分类方式中哪一种方式最适合呢？我们希望分割方法有一定的冗余度，也就是padding，因为我们无法保证新的样本一定能准确的落入已有样本的「闭包」（这里的闭包closure，是拓扑学概念，即一个拓扑空间里，子集S的闭包由S 的所有点及S 的极限点所组成的一个集合；直观上来说，即为所有“靠近”S 的点所组成的集合。）

所以对于上面的样本分类，我们希望的是找到类1与类2相邻边界的样本点，并以这些边界点出发找到一个最宽的区域，或边界（maximum margin），而构成这样区域的「边界点」，就是支持向量（support vectors）。例如下图所示：

在找到宽度最大的margin后，我们就可以从margin中找到最适分界区的中线位置，也就是分割不同分类的超平面（hyperplane）。之所以称它叫hyperplane，是因为当分类任务是高纬的，此时hyperplane就会从二维的线变成了一个不规则平面，可以是马鞍面，或其他什么形式。我们要求hyperplane到margin的边界的距离是一样的，这样可以保证最大冗余度。

所以，我们可以知道，该算法的核心就是为不同分类找到最合适的 hyperplane。那么什么时候hyperplane才是一个面呢，这取决于我们的样本使用的的标签或特征数，当样本只有两个特征时 hyperplane 在二维平面内表现为一根线，但是当特征数增加到三个以上时，它就会表现为一个平面。

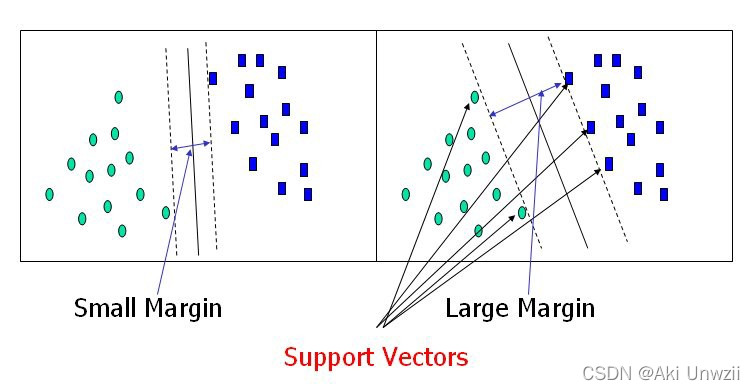
于是你会发现一个问题，如何确定 support vector，会直接影响到 hyperplane 的位置和 margin 的大小，就像是上面这个例子一样。所以对于该算法来说，我们的问题变为了如何有效的到最大的 margin。

背后的数学思想

上面这些内容是 SVM 的求解思路，接下来我们需要来考虑如何把这个过程用数学的语言进行描述。

支持向量的数学定义

首先，我们要思考怎么定义一个结构可能很复杂的 hyperplane，用一般的数学手段是难以找到符合预期的方程。所以，我们可以这样考虑问题，使用最简单的线性方程组来表示这个超平面，即：

$$\sum [\mathbf{w}\cdot \mathbf{x}+b]=0$$

这里，先不必关心在其他教材中提到的法向量等问题，我们只需要理解 $\mathbf{w}$ 类似于斜率或权重，$\mathbf{x}$ 是超平面上的点，而 $b$ 是位移量或偏差量即可。这样，对于超平面两侧约束该超平面支撑向量所在的平面，就可以通过对超平面使用位移偏量 $\pm C$ 的形式进行表示：

$$\{\begin{array}{c}w\cdot x_a+b=+C\\ w\cdot x_b+b=-C\end{array}$$

于是我们接下来可以这样做

$$\Rightarrow \{\begin{array}{c}\frac{w}{C}\cdot x_a+\frac{b}{C}=+1\\ \frac{w}{C}\cdot x_a+\frac{b}{C}=-1\end{array}\Rightarrow \{\begin{array}{c}\mathbf{w}\cdot x_a+b=+1\\ \mathbf{w}\cdot x_a+b=-1\end{array}$$

于是正负超平面的 margin，就可以直接通过上式减下式，得到

$$\mathbf{w}\cdot (x_a-x_b)=2\Rightarrow \Vert \mathbf{w}\Vert \cdot \Vert x_a-x_b\Vert \cdot \cos \theta =2$$

继而可以得到它们之间的距离，比如通过投影得到 $L$ 为

$$L=\Vert x_a-x_b\Vert \cdot \cos \theta$$

带回原式，得到

$$L\cdot \Vert \mathbf{w}\Vert =2\to L=\frac{2}{\Vert \mathbf{w}\Vert }$$

这样，我们得到了正、负超平面边界（蓝色和绿色虚线），决策超平面（中间红色实线）、以及正负面之间 margin 的宽度这几个公式。

通过上述的计算过程，我们发现，划分超平面的问题，可以变成如何找到最大 margin 的问题，也就是 margin 求极限问题，即

$$\underset{\Vert w\Vert \to 0}{\lim }\frac{2}{\Vert \mathbf{w}\Vert }\to \max \frac{2}{\Vert \mathbf{w}\Vert }$$

也就是尽可能找到最小的 $\Vert \mathbf{w}\Vert$，用数学的语言进行描述即：

$$\max \frac{2}{\Vert \mathbf{w}\Vert },y_i\cdot ({\mathbf{w}}^T\cdot {\mathbf{x}}_i+b)\ge 1,fori=1,\cdots ,n$$

另一方面，我们找到了对于两个不同类型数据对于超平面的约束条件，即：

$$\{\begin{array}{cc}{\mathbf{w}}^{\mathbf{T}}\cdot {\mathbf{x}}_{\mathbf{i}}+b\ge +1& y_i=+1\\ {\mathbf{w}}^{\mathbf{T}}\cdot {\mathbf{x}}_{\mathbf{i}}+b\le -1& y_i=-1\end{array}$$

到这里，关于支持向量与超平面的基本数学定义已经清楚。接下来，我们需要讨论怎么做能找到理想的 $\mathbf{w}$ 和 $b$，也就是如何使用到梯度下降算法，帮助我们找到合适的取值。

Hinge Loss 与梯度下降算法

Hinge Loss 国内一般译作「铰链损失函数」或「合页损失函数」，它是一种十分重要的机器学习基本损失函数。在SVM中，也同样用到了这个损失函数作为模型的评价标准，它的形式如下：

$$C({\vec{x}}_i,y_i,f({\vec{x}}_i){)}_{+}=\{\begin{array}{cc}0& if{y}_i\cdot (\vec{w}\cdot \vec{x}+b)\ge 1\\ 1-y_i\cdot (\vec{w}\cdot \vec{x}+b)& else\end{array}$$

或者，表示成如下形式：

$$\max \left(0,1-y_i\cdot (\vec{w}\cdot \vec{x}+b)\right)$$

请先记住，它的函数图像为如下形式

现在我们看看如何与梯度下降联系在一起。首先我们假设，参与分类的样本没有异常存在，也就是说我们先不考虑一些特殊的情况，即「绝对理想条件下」。

由于上述 Loss 方程在分类结果与目标一致不惩罚（即分类结果的正负号与目标一致），在分类错误时执行线性的惩罚，所以我们可以依靠这样的一个特点找到最大的 margin，所以有：

L = ∑ i = 1 n max ⁡ { 0 , 1 − ( w T x i + b ) ⋅ y i } L = \sum_{i=1}^n \max \{ 0, 1 - (w^T x_i + b) \cdot y_i \} L=i=1∑n​max{0,1−(wTxi​+b)⋅yi​}

但是这样并不能得到最优解，所以我们会再考虑加上一个限制条件，于是上式被改写为

L = ∑ i = 1 n λ i max ⁡ { 0 , 1 − ( w T x i + b ) ⋅ y i } + 1 2 ∥ w ∥ 2 L = \sum_{i=1}^n \lambda_i \max \{ 0, 1 - (w^T x_i + b) \cdot y_i \} + \frac{1}{2} \| w \|^2 L=i=1∑n​λi​max{0,1−(wTxi​+b)⋅yi​}+21​∥w∥2

需要注意，原始的 hinge loss 只对错误的部分进行惩罚，于是接下来我们只讨论错误的分类部分，对于 $\frac{\partial L}{\partial w}$ 部分：
$$\frac{\partial L}{\partial w}=\mathbf{w}-\sum _{i=1}^n{\lambda }_i{y}_i{\mathbf{x}}_i$$

而 $\frac{\partial L}{\partial b}$ 为

$$\frac{\partial L}{\partial b}=\sum _{i=1}^n{\lambda }_i{y}_i$$

然后我们再代入梯度下降更新公式，得到：

$$\{\begin{array}{c}{w}^{\ast }=w-\alpha \cdot \frac{\partial L}{\partial w}\\ \\ b^{\ast }=b-\alpha \cdot \frac{\partial L}{\partial b}\end{array}$$

这里的 $\alpha$ 就是「学习率」。到这一步，我们基本上可以通过梯度下降算法让模型自动更新参数。尽管看起来很复杂，但是可以用简单的方式实现，比如一个常见的 Stochastic Gradient Descent 算法，用伪代码实现如下：

软间隔与硬间隔

现在我们来讨论一些来自特殊样本导致的分类问题。由于在实际过程中，可能会有数个样本的特征和它应该归属的族有很大差异，比如在女性样本中不排除男性化特征明显的女性，以及男性样本中出现女性化特征明显的男性，但由于我们判定一个样本属于男性还是女性的依据是根据DNA或者某些器官进行判定，所以就会在统计时出现下面这样的情况。

如果我们一定要求男性样本归属男性群体，女性样本归属女性群体，那么对于上面这个情况要找到适合的超平面以及足够的margin就非常困难，而这种划分方式被称为 —— 硬间隔。它使得模型的容错率很低，并且很容易出现过拟合的问题而导致精度降低。

对应的，我们容许一定的例外样本存在，并且不考虑它对整体样本划分的影响，这种划分形式就是软间隔了。所以对于Hinge Loss，我们可以做如下改变，使得它具备一定的容错性：

$$L=\min \left[\frac{1}{2}\Vert w{\Vert }^2+C\sum _{i=1}^n{\xi }_i\right]$$

这里的C相当于一个阀门，当C趋向无穷大时，它会导致Hinge Loss倾向 硬间隔，而C非常小的时候，就会表现出 软间隔 的特性。

参考资料

• Support Vector Machine — Introduction to Machine Learning Algorithms, Rohith Gandhi https://towardsdatascience.com/support-vector-machine-introduction-to-machine-learning-algorithms-934a444fca47
• https://zh.wikipedia.org/wiki/%E6%94%AF%E6%8C%81%E5%90%91%E9%87%8F%E6%9C%BA#%E7%8E%B0%E4%BB%A3%E6%96%B9%E6%B3%95
• https://zhuanlan.zhihu.com/p/40284001