机器学习实战，探秘基于支持向量机的小麦种子分类：让每颗小麦种子“无所遁形”（附实验全流程+全部源代码）

在机器学习的广袤天地里，支持向量机（SVM）宛如一颗久经岁月却依旧璀璨的明星。尽管如今它被视作传统的机器学习技术，但在小麦种子分类这个特定领域，它却有着不可小觑的力量。小麦，作为世界粮食体系中的重要成员，其种子质量直接关系到作物的产量和品质。传统的小麦种子分类方法往往依赖于人工经验，效率低且准确性难以保证。而支持向量机，凭借其坚实的数学理论基础，犹如一位严谨的裁判，在小麦种子分类的舞台上发挥着独特的作用。今天，就让我们一同探究基于支持向量机的小麦种子分类的奥秘。

一、实验目的

本实验通过支持向量机完成对小麦种子进行分类，以及对比不同特征缩放及核函数对支持向量机分类表现的影响，同时掌握一对多和一对一分类的应用。具体可分为：

（1）掌握对数据集的读取和基本预处理步骤，例如特征缩放和数据集划分。

（2）理解线性SVM模型的原理和使用方法，能够通过训练并预测得到准确率较高的分类结果，并能可视化分类结果

（3）了解了特征组合对分类准确率的影响

（4）学会使用PCA进行数据降维，将高维数据可视化到二维平面，并使用降维后的数据进行分类预测，观察分类效果。

（5）理解高斯核函数在非线性分类任务中的应用，能够使用高斯核函数创建非线性SVM模型，并进行分类预测和可视化。

（6）掌握一对多和一对一分类的基本思想和实现方法，能够应用于多分类问题的处理中，并可视化分类结果。

二、实验原理

在本实验中，我们使用了UCI Machine Learning Repository（UCI机器学习库）提供的小麦种子数据集。数据预处理是指将原始数据转换为模型能够使用的格式。在本实验中，我们使用pandas库读入csv格式数据，并将特征的均值和标准差进行转换，使得特征的值按照标准正态分布进行缩放。将不同特征的值范围映射到相似的尺度上，便于模型构建。

1.支持向量机

（1）二分类支持向量机

①线性可分情况

对于二分类任务，SVM的目标是找到一个最优的超平面，能够在特征空间中将正类和负类样本分割开。这个超平面被定义为两个平行的、距离最远的支持向量构成的间隔最大化的超平面。支持向量是离超平面最近的样本点，它们决定了超平面的位置和方向。

在训练过程中，SVM通过最小化结构风险函数来找到最优的超平面，常用的方式是使用拉格朗日乘子法以及核函数来处理线性不可分情况。

②线性不可分情况

对于线性不可分的情况，SVM采用核函数的方式将样本映射到高维特征空间中，从而将其线性分割。常用的核函数有线性核函数、多项式核函数和高斯核函数等。

在高维特征空间中，SVM仍然寻找一个超平面来将样本分割，并通过支持向量来确定超平面的位置和方向。在决策阶段，它会将新样本映射到特征空间，再根据超平面将其分类。

（2）多分类支持向量机

①一对一（One-vs-One）方法

对于K个类别，构建K*(K-1)/2个分类器，每个分类器用来区分两个不同的类别。在预测时，将样本输入到所有分类器中，统计每个类别的投票结果，最终将得票数最多的类别作为预测结果。

②一对多（One-vs-Rest）方法

对于K个类别，构建K个分类器，每个分类器用来区分一个类别和其他剩余的类别。在预测时，将样本输入到所有分类器中，选择具有最高分类分数的类别作为预测结果。

2.PCA

PCA（Principal Component Analysis，主成分分析）是一种常用于数据降维的无监督机器学习算法，它可以将高维数据映射到低维空间中，保留最重要的特征，以尽量保留原始数据的信息，从而实现对数据的降维和可视化。

PCA通过找到数据中最具有代表性的主成分来实现降维。主成分是指对数据中包含的信息进行解释的方向，它们是与数据的方差有关的方向。在一个n维数据集中，主成分是n个正交的方向，它们按照降序排列，每个方向都隐含着尽可能多的数据方差。

PCA算法可以减少训练数据的维度和特征数量并减少计算和存储成本，进而加快算法的训练速度，提高模型的准确性和鲁棒性。

三、实验数据收集

数据集选取自网站Car Evaluation - UCI Machine Learning Repository，使用了seed_dataset.data数据。

该数据集有七个特征分别为：Area（区域），Perrmeter（周长），Compactness（压实度），Kernel_Length（籽粒长度），Kernel_Width（籽粒宽度），Asymmetry_Coefficient（不对称系数），Kernel_Groove_Length（籽粒腹沟长度），为了方便处理，代码中可视化时分别以下标0-6代表这七个特征，一个标签，包含小麦种子的三种类别，分别为1（Kama），2（Rosa），3（Canadian）。

四、实验环境

在实验过程中，使用了以下工具和库：

Python编程语言

Jupyter Notebook环境

Pandas库和Numpy库：读取seeds_dataset.data数据集并对数据集进行处理和分析。

Scikit-learn库：用于机器学习算法的建模和评估，包括特征缩放和标准化的操作，支持向量机模型、一对一分类器、一对多分类器的构建，模型的训练和评估，衡量模型的性能和预测结果的准确性。

Matplotlib库：可视化分类效果（决策边界，支持向量，训练样本）。

五、实验步骤

1.数据处理

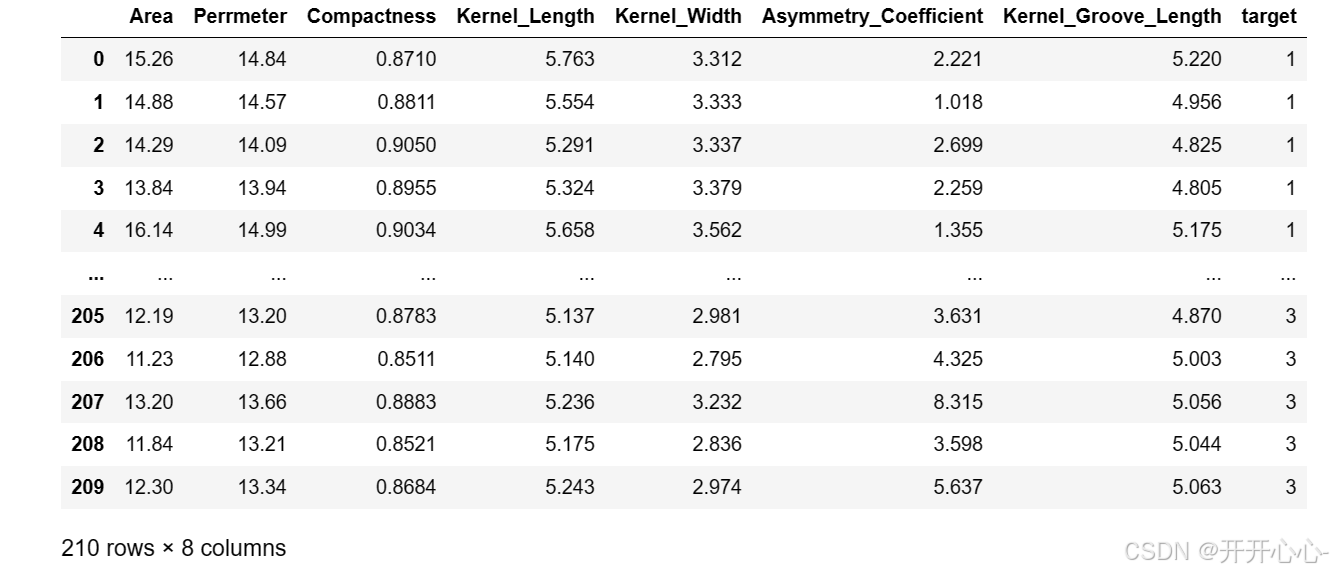
（1）读取小麦种子数据集，检查有无缺失值，为列加上对应属性和标签。处理后数据如下：

（2）选择特征并进行缩放，随机选取两个特征，未处理前：

如果特征的尺度差异较大，可能会导致支持向量机对某些特征更加敏感，而对其他特征忽略。因此使用StandardScaler根据特征的均值和标准差进行转换，使得特征的值按照标准正态分布进行缩放。

将不同特征的值范围映射到相似的尺度上，以保证不同特征对这些算法的影响更加均衡，从而提高模型的性能和稳定性。处理后：

（3）划分训练集和测试集。将数据集划分为训练集和测试集，用于模型训练和性能评估。在

本次实验中一共有210个数据，随机选取168个作为训练集，42个数据作为测试集，比例为4：1。

2.线性SVM模型分析

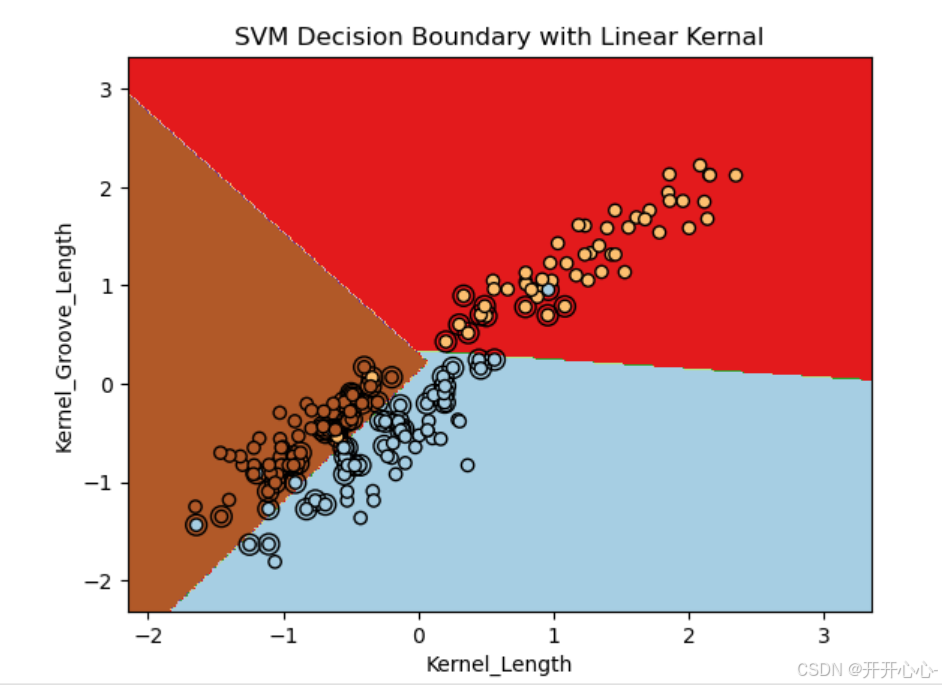
（1）创建线性SVM模型

随机选取两个特征创建sklearn.svm中的支持向量机模型，指定模型的核函数为线性核，指定模型的正则化参数为0.45，然后对训练集进行训练，对测试集进行预测并输出结果和正确率。

接着对训练集的分类结果进行可视化，包括决策边界，样本点和支持向量。可视化效果如下：

（2）将所有特征两两组合

由（1）可知我们只是随机选择了两个特征，不具有普遍性，因此我们将所有的特征两两组合分别给出预测的正确率，然后对正确率最高的前六组分类结果进行可视化，可视化如下：

（3）PCA降维预测

虽然有的特征正确率很高，但是大多数的预测结果为80%甚至还有60%的，说明随机选取特征损失了一些重要特征从而降低了预测的正确性，因此将七个特征进行PCA降维变成二维特征向量。

原始数据：

降维后数据：

降维后和我们前面的操作一致，建立支持向量机模型，预测结果然后进行可视化，结果如下：

3.高斯核函数模型

（1）创建高斯核函数SVM模型

指定模型的核函数为高斯核，指定模型的正则化参数为0.45，后对训练集进行训练，对测试集进行预测并输出结果和正确率。

分类结果可视化：

（2）所有特征两两组合

将所有特征两两组合分别训练新的高斯核函数支持向量机模型并进行预测，然后对正确率最高的前六组进行可视化：

（2）PCA降维预测

和线性核函数的操作一样，将七个特征进行PCA降维变成二维特征向量，然后建立支持向量机模型，预测结果然后进行可视化，结果如下：

4.拓展

前面我们通过PCA将七维向量降至二维，高斯核函数和线性核函数的效果还不错，但是全部是在二维向量的基础上进行操作的，不禁让人好奇，三维时预测效果又是怎样的呢，因此尝试将七维向量降至三维，进行预测和可视化。预测结果时和二维操作一致，三个特征时，应用线性核函数和高斯核函数得到的正确率均为90%，均取得较好效果，可视化时我们import Axes3D库进行3D可视化，三个特征作为x,y,z轴，可视化效果如下：

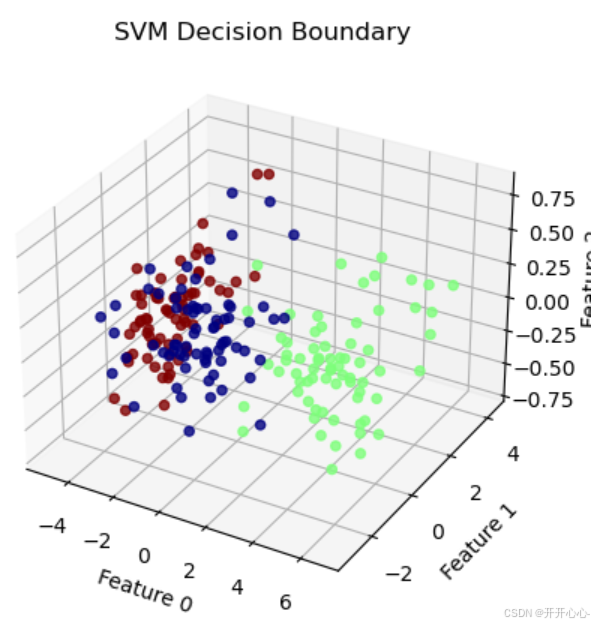
从图中我们可以看出在3D效果下的可视化并不是太清晰，因此我们import FuncAnimation库进行动态旋转，使可视化效果更加直观。效果如下:

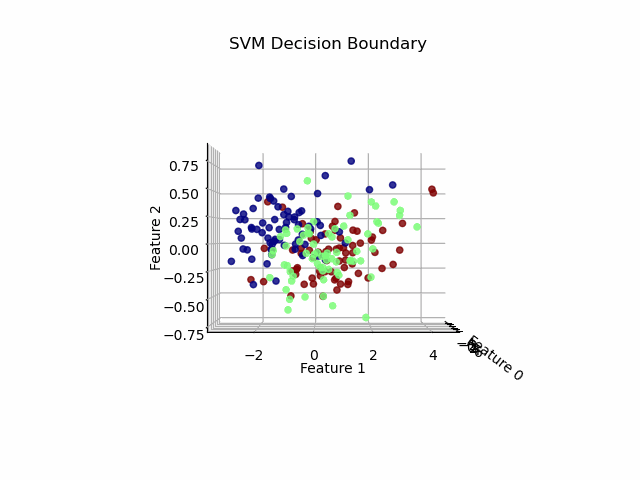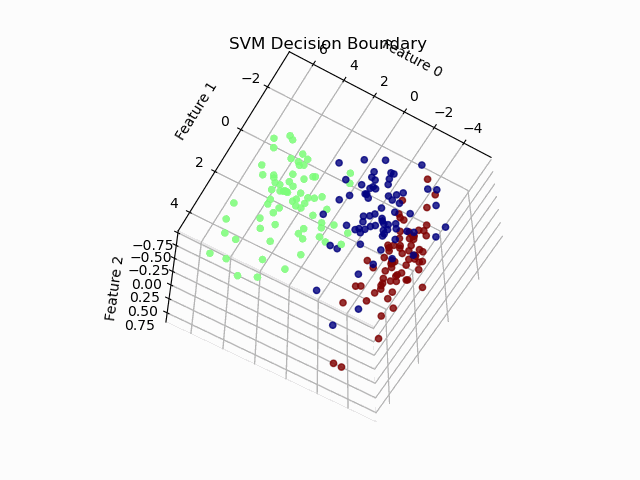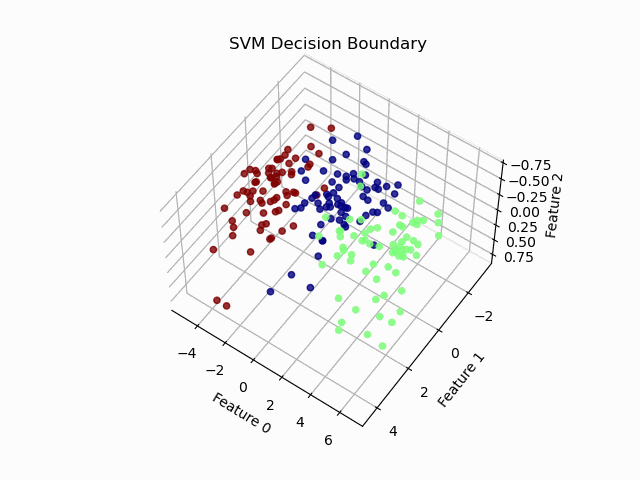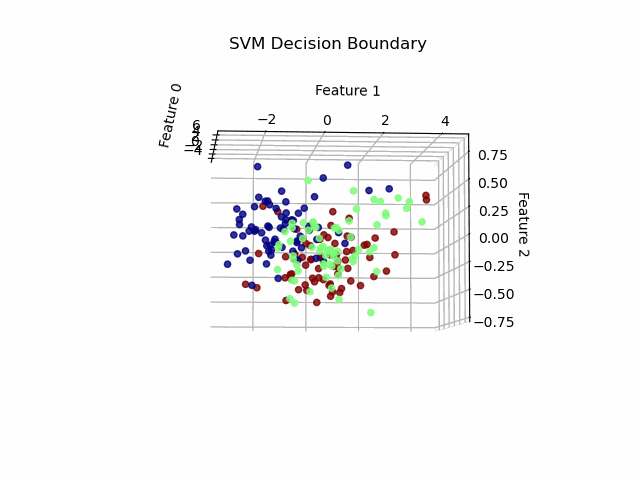
六、实验结果分析

1.随机特征组合

通过将所有特征进行两两组合，分别训练支持向量机模型，并预测准确率，正确率如下：

其中0-7分别对应为：Area（区域），Perrmeter（周长），Compactness（压实度），Kernel_Length（籽粒长度），Kernel_Width（籽粒宽度），Asymmetry_Coefficient（不对称系数），Kernel_Groove_Length（籽粒腹沟长度）。

从图中我们可以看出线性核函数预测正确率范围在0.69-0.95，高斯核函数预测正确率范围在0.69-0.97，选取不同的特征组合对实验结果的影响较大，特征（2，5）即压实度和不对称系数的特征组合预测正确率的效果较差，正确率只有69%，而特征（3，6)即籽粒长度和籽粒腹沟长度的特征组合预测正确率的效果较好，达到了95%-97%，模型更稳定，泛化能力更强。而选择的核函数不同，得到的结果也不尽相同，有的特征组合线性核函数预测效果比高斯核函数好，比如特征（0，2）、（1，2）、（2，3）等，而这些特征都有特征2即压实度，说明压实度特征更适合线性模型，而有的特征组合高斯核函数更好比如特征（0，6），（1，6）等，其中特征（1，6）组合正确率高达97%，已经具备较好的预测效果，说明特征6即籽粒腹沟长度更适合高斯核函数进行分类。

2.PCA降维分析

虽然随机选取两个特征进行建模可行，但是可能对数据的整体结构和表达能力造成较大的损失。如果数据中的特征之间存在一定的相关性或者包含了重要的信息，则直接随机选取两个特征可能无法充分利用数据中的信息。而PCA降维可以通过线性变换，将原始数据映射到一个最大可分辨性的新特征空间，保留了更多的信息。因此将七个特征向量由七维降至二维，训练新的线性核函数模型和高斯核函数模型，分别进行预测，结果如下：

特征随机组合时线性核函数正确率在69%-95%，平均正确率为83%，高斯核函数正确率在69%-97%，平均正确率为83%，而降维后的预测正确率分别为90%和85%，均比平均正确率要高，因此，PCA降维的方法能够更好地保持数据的结构和信息，提升模型的性能和泛化能力。而对于小麦种子的分类任务中使用线性核函数的预测效果更好。

七、多分类支持向量机

多分类支持向量机模型选取的特征是由PCA降维后的包含所有特征信息的二维特征向量。

1.一对一分类

（1）线性核函数

使用OneVsOneClassifier包装SVC模型，其中kernel='linear’指定线性核函数，进行预测和可视化。可视化结果如下：

（2）高斯核函数

使用OneVsOneClassifier包装SVC模型，其中kernel='rbf’指定高斯核函数，进行预测和可视化。可视化结果如下：

2.一对多分类

（1）线性核函数

使用OneVsRestClassifier包装SVC模型，其中kernel='linear’指定线性核函数，进行预测和可视化。可视化结果如下：

（2）高斯核函数

使用OneVsRestClassifier包装SVC模型，其中kernel='linear’指定线性核函数，进行预测和可视化。可视化结果如下：

经过对四种情况的可视化，我们可以发现多分类支持向量机预测效果也均在85%以上，通过对不同分类方式的比较，一对一分类模型分类效果更好，通过对核函数的比较，线性核函数的分类效果更好，但是这四种预测结果最高才90%，与随机选取特征时的95%-97%还有较大差距，因此，可能需要进一步优化，包括对一些模型超参数的调整，降维方法的改善等。

八、全部源代码

# 导入库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from sklearn.multiclass import OneVsRestClassifier
from sklearn.multiclass import OneVsOneClassifier
from itertools import combinations
from sklearn.feature_selection import SelectKBest, f_regression
from sklearn.decomposition import PCA
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.animation import FuncAnimation
# 读取数据
data = pd.read_csv('seeds_dataset.data', header=None, delimiter=' ')
# 数据处理
data.columns=["Area","Perrmeter",'Compactness','Kernel_Length','Kernel_Width','Asymmetry_Coefficient','Kernel_Groove_Length','target']

X = np.array(data.iloc[:, :-1])
y = np.array(data.iloc[:, -1])
# 随机选择两个特征
random_features = [3, 6]  # 这里选择第二个和第七个特征
X_selected = X[:, random_features]

# 特征缩放
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X_selected)

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42)
# 线性模型
# 创建支持向量机模型
svm = SVC(kernel='linear', C=0.45)
svm.fit(X_train, y_train)

# 在测试集上进行预测
y_pred = svm.predict(X_test)
print("预测结果",y_pred)
# 分析预测结果
accuracy = svm.score(X_test, y_test)
print("预测准确率:", accuracy)

# 可视化决策边界
x_min, x_max = X_scaled[:, 0].min() - 0.5, X_scaled[:, 0].max() + 1
y_min, y_max = X_scaled[:, 1].min() - 0.5, X_scaled[:, 1].max() + 1
h = 0.02  # 步长
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
Z = svm.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=plt.cm.Paired)

# 在决策边界上绘制支持向量
plt.scatter(svm.support_vectors_[:, 0], svm.support_vectors_[:, 1], facecolors='none', edgecolors='k', marker='o', s=100)

# 绘制训练样本点
plt.scatter(X_train[:, 0], X_train[:, 1], c=y_train, edgecolors='k', cmap=plt.cm.Paired)
plt.xlabel(data.columns[3])
plt.ylabel(data.columns[6])
plt.title('SVM Decision Boundary with Linear Kernal')
plt.show()
# 所有特征随机组合可视化正确率最高的前六组
# 特征缩放
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# 获取特征数量
num_features = X.shape[1]

# 保存最好的六个特征组合及其对应的准确率
top_six_features = []
top_six_accuracies = []
sum=0
feature_names = ["Area", "Perimeter", "Compactness", "Kernel Length", "Kernel Width", "Asymmetry Coefficient", "Kernel Groove Length"]

# 遍历所有特征两两组合
for i in range(num_features):
    for j in range(i+1, num_features):
        # 选择两个特征
        selected_features = [i, j]
        X_selected = X_scaled[:, selected_features]
        
        # 划分训练集和测试集
        X_train, X_test, y_train, y_test = train_test_split(X_selected, y, test_size=0.2, random_state=42)
        
        # 创建支持向量机模型
        svm = SVC(kernel='linear', C=0.45)
        svm.fit(X_train, y_train)
        
        # 在测试集上进行预测
        y_pred = svm.predict(X_test)
        
        # 计算预测准确率
        accuracy = svm.score(X_test, y_test)
        
        # 保存准确率及对应的特征组合
        top_six_features.append(selected_features)
        top_six_accuracies.append(accuracy)
        print(f"特征组合 ({i}, {j}) 预测准确率: {accuracy}")
        sum+=accuracy
print("平均正确率：",sum/21)
# 取准确率最高的前六个特征组合
top_six_indices = np.argsort(top_six_accuracies)[-6:]
top_six_features = [top_six_features[i] for i in top_six_indices]

# 绘制可视化
plt.figure(figsize=(12, 8))
for idx, features in enumerate(top_six_features):
    # 选择特征
    X_selected = X_scaled[:, features]
    
    # 划分训练集和测试集
    X_train, X_test, y_train, y_test = train_test_split(X_selected, y, test_size=0.2, random_state=42)
    
    # 创建支持向量机模型
    svm = SVC(kernel='linear', C=0.45)
    svm.fit(X_train, y_train)
    
    # 网格化预测结果
    x_min, x_max = X_selected[:, 0].min() - 0.5, X_selected[:, 0].max() + 1
    y_min, y_max = X_selected[:, 1].min() - 0.5, X_selected[:, 1].max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02), np.arange(y_min, y_max, 0.02))
    Z = svm.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)

    # 绘制决策边界和训练样本点
    plt.subplot(2, 3, idx+1)
    plt.contourf(xx, yy, Z, cmap=plt.cm.Paired)
    plt.scatter(X_train[:, 0], X_train[:, 1], c=y_train, edgecolors='k', cmap=plt.cm.Paired)
    # 计算分类器的准确率
    test_acc = svm.score(X_test, y_test)
    plt.xlabel('{}'.format(feature_names[features[0]]))
    plt.ylabel('{}'.format(feature_names[features[1]]))
    plt.title(f'Linear SVM Accuracy: {round(test_acc*100,3)}% ')
plt.tight_layout()

plt.show()
# 线性核函数PCA分析
# 对七个特征进行降维

# 使用PCA进行降维
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)

# 划分训练集和测试集
X_train_pca, X_test_pca, y_train_pca, y_test_pca = train_test_split(X_pca, y, test_size=0.2, random_state=42)

# 创建支持向量机模型
svm_pca = SVC(kernel='linear', C=0.45)
svm_pca.fit(X_train_pca, y_train_pca)
# 在测试集上进行预测
y_pred_pca = svm_pca.predict(X_test_pca)

# 分析预测结果
accuracy_pca = svm_pca.score(X_test_pca, y_test_pca)
print("线性核函数预测准确率(降维后):", accuracy_pca)

# 可视化决策边界
x_min_pca, x_max_pca = X_pca[:, 0].min() - 0.5, X_pca[:, 0].max() + 1
y_min_pca, y_max_pca = X_pca[:, 1].min() - 0.5, X_pca[:, 1].max() + 1
h_pca = 0.02  # 步长
xx_pca, yy_pca = np.meshgrid(np.arange(x_min_pca, x_max_pca, h_pca), np.arange(y_min_pca, y_max_pca, h_pca))
Z_pca = svm_pca.predict(np.c_[xx_pca.ravel(), yy_pca.ravel()])
Z_pca = Z_pca.reshape(xx_pca.shape)
plt.contourf(xx_pca, yy_pca, Z_pca, cmap=plt.cm.Paired)

# 在决策边界上绘制支持向量
plt.scatter(svm_pca.support_vectors_[:, 0], svm_pca.support_vectors_[:, 1], facecolors='none', edgecolors='k', marker='o', s=100)

# 绘制训练样本点
plt.scatter(X_train_pca[:, 0], X_train_pca[:, 1], c=y_train_pca, edgecolors='k', cmap=plt.cm.Paired)
plt.xlabel('PCA Component 1')
plt.ylabel('PCA Component 2')
plt.title('PCA_SVM Decision Boundary')
plt.show()
# 随机选择两个特征
random_features = [3, 6]  # 这里选择第一个和第六个特征
X_selected = X[:, random_features]

# 特征缩放
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X_selected)
# 应用高斯核函数分类
# 创建支持向量机模型并使用高斯核函数
svm = SVC(kernel='rbf', C=0.45)
svm.fit(X_train, y_train)
# 在测试集上进行预测
y_pred = svm.predict(X_test)
print("预测结果：",y_pred)
# 分析预测结果
accuracy = svm.score(X_test, y_test)
print("预测准确率:", accuracy)

# 可视化决策边界
# 获取边界限制
x1_min, x1_max = X_scaled[:, 0].min() - 0.5, X_scaled[:, 0].max() + 0.5
x2_min, x2_max = X_scaled[:, 1].min() - 0.5, X_scaled[:, 1].max() + 0.5

# 生成网格点
h = 0.02
x1, x2 = np.meshgrid(np.arange(x1_min, x1_max, h), np.arange(x2_min, x2_max, h))

# 进行预测并绘制结果
Z = svm.predict(np.c_[x1.ravel(), x2.ravel()])
Z = Z.reshape(x1.shape)
plt.contourf(x1, x2, Z, cmap=plt.cm.Paired, alpha=1)

# 绘制训练样本点
plt.scatter(X_scaled[:, 0], X_scaled[:, 1], c=y, edgecolors='k',alpha=1, cmap=plt.cm.Paired)
plt.xlabel(data.columns[3])
plt.ylabel(data.columns[6])
plt.title('SVM Decision Boundary with RBF Kernel')
plt.show()
# 所有特征随机组合应用高斯核函数，可视化正确率最高的前六组
X = np.array(data.iloc[:, :-1])
y = np.array(data.iloc[:, -1])
# 特征缩放
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# 获取特征数量
num_features = X_scaled.shape[1]

# 保存最好的六个特征组合及其对应的准确率
top_six_features = []
top_six_accuracies = []
sum=0
# 遍历所有特征两两组合
for i in range(num_features):
    for j in range(i+1, num_features):
        # 选择两个特征
        selected_features = [i, j]
        X_selected = X_scaled[:, selected_features]
        
        # 划分训练集和测试集
        X_train, X_test, y_train, y_test = train_test_split(X_selected, y, test_size=0.2, random_state=42)
        
        # 创建支持向量机模型
        svm = SVC(kernel='rbf', C=0.45)
        svm.fit(X_train, y_train)
        
        # 在测试集上进行预测
        y_pred = svm.predict(X_test)
        
        # 计算预测准确率
        accuracy = svm.score(X_test, y_test)
        
        # 保存准确率及对应的特征组合
        top_six_features.append(selected_features)
        top_six_accuracies.append(accuracy)
        print(f"特征组合 ({i}, {j}) 预测准确率: {accuracy}")
        sum+=accuracy
print("平均正确率：",sum/21)
# 取准确率最高的前六个特征组合
top_six_indices = np.argsort(top_six_accuracies)[-6:]
top_six_features = [top_six_features[i] for i in top_six_indices]

# 绘制可视化
plt.figure(figsize=(12, 8))
for idx, features in enumerate(top_six_features):
    # 选择特征
    X_selected = X_scaled[:, features]
    
    # 划分训练集和测试集
    X_train, X_test, y_train, y_test = train_test_split(X_selected, y, test_size=0.2, random_state=42)
    
    # 创建支持向量机模型
    svm = SVC(kernel='rbf', C=0.45)
    svm.fit(X_train, y_train)
    
    # 网格化预测结果
    x_min, x_max = X_selected[:, 0].min() - 0.5, X_selected[:, 0].max() + 1
    y_min, y_max = X_selected[:, 1].min() - 0.5, X_selected[:, 1].max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02), np.arange(y_min, y_max, 0.02))
    Z = svm.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    
    # 绘制决策边界和训练样本点
    plt.subplot(2, 3, idx+1)
    plt.contourf(xx, yy, Z, cmap=plt.cm.Paired)
    plt.scatter(X_train[:, 0], X_train[:, 1], c=y_train, edgecolors='k', cmap=plt.cm.Paired)
    # 计算分类器的准确率
    test_acc = svm.score(X_test, y_test)
    plt.xlabel('{}'.format(feature_names[features[0]]))
    plt.ylabel('{}'.format(feature_names[features[1]]))
    plt.title(f'RBF SVM Accuracy: {round(test_acc*100,3)}% ')

plt.tight_layout()
plt.show()
# 高斯核函数PCA分析
# 创建支持向量机模型
svm_pca = SVC(kernel='rbf', C=0.45)
svm_pca.fit(X_train_pca, y_train_pca)
# 在测试集上进行预测
y_pred_pca = svm_pca.predict(X_test_pca)

# 分析预测结果
accuracy_pca = svm_pca.score(X_test_pca, y_test_pca)
print("高斯核函数预测准确率(降维后):", accuracy_pca)

# 可视化决策边界
x_min_pca, x_max_pca = X_pca[:, 0].min() - 0.5, X_pca[:, 0].max() + 1
y_min_pca, y_max_pca = X_pca[:, 1].min() - 0.5, X_pca[:, 1].max() + 1
h_pca = 0.02  # 步长
xx_pca, yy_pca = np.meshgrid(np.arange(x_min_pca, x_max_pca, h_pca), np.arange(y_min_pca, y_max_pca, h_pca))
Z_pca = svm_pca.predict(np.c_[xx_pca.ravel(), yy_pca.ravel()])
Z_pca = Z_pca.reshape(xx_pca.shape)
plt.contourf(xx_pca, yy_pca, Z_pca, cmap=plt.cm.Paired)

# 在决策边界上绘制支持向量
plt.scatter(svm_pca.support_vectors_[:, 0], svm_pca.support_vectors_[:, 1], facecolors='none', edgecolors='k', marker='o', s=100)

# 绘制训练样本点
plt.scatter(X_train_pca[:, 0], X_train_pca[:, 1], c=y_train_pca, edgecolors='k', cmap=plt.cm.Paired)
plt.xlabel('PCA Component 1')
plt.ylabel('PCA Component 2')
plt.title('PCA_SVM Decision Boundary')
plt.show()
# 对七个特征进行降维，降至三维
X = np.array(data.iloc[:, :-1])
y = np.array(data.iloc[:, -1])

# 使用PCA进行降维
pca = PCA(n_components=3)
X_pca = pca.fit_transform(X)

X_train, X_test, y_train, y_test = train_test_split(X_pca, y, test_size=0.2, random_state=42)

svm = SVC(kernel='linear', C=1.2)
svm.fit(X_train, y_train)

y_pred = svm.predict(X_test)

accuracy = svm.score(X_test, y_test)
print("预测准确率:", accuracy)

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

xx = X_pca[:, 0]
yy = X_pca[:, 1]
zz = X_pca[:, 2]

c = y # 创建一个与数据点数量相同的数组

scatter = ax.scatter(xx, yy, zz, c=c,alpha=0.8, cmap=plt.cm.jet)

ax.set_xlabel('Feature 0')
ax.set_ylabel('Feature 1')
ax.set_zlabel('Feature 2')
ax.set_title('SVM Decision Boundary')


def update(num, scatter, ax):
    ax.view_init(elev=num, azim=num)
    return scatter,

ani = FuncAnimation(fig, update, frames=range(0, 360, 5), fargs=(scatter, ax), interval=50)

# 保存动画
ani.save('3d_animation.gif', writer='imagemagick')

plt.show()
# 使用PCA进行降维
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)

X_train, X_test, y_train, y_test = train_test_split(X_pca, y, test_size=0.2, random_state=42)
# 一对一线性核函数分类
# 创建支持向量机模型
svm_pca = OneVsOneClassifier(SVC(kernel='linear', C=0.45))
svm_pca.fit(X_train_pca, y_train_pca)
# 在测试集上进行预测
y_pred_pca = svm_pca.predict(X_test_pca)

# 分析预测结果
accuracy_pca = svm_pca.score(X_test_pca, y_test_pca)
print("预测准确率(降维后):", accuracy_pca)

# 可视化决策边界
x_min_pca, x_max_pca = X_pca[:, 0].min() - 0.5, X_pca[:, 0].max() + 1
y_min_pca, y_max_pca = X_pca[:, 1].min() - 0.5, X_pca[:, 1].max() + 1
h_pca = 0.02  # 步长
xx_pca, yy_pca = np.meshgrid(np.arange(x_min_pca, x_max_pca, h_pca), np.arange(y_min_pca, y_max_pca, h_pca))
Z_pca = svm_pca.predict(np.c_[xx_pca.ravel(), yy_pca.ravel()])
Z_pca = Z_pca.reshape(xx_pca.shape)
plt.contourf(xx_pca, yy_pca, Z_pca, cmap=plt.cm.Paired)

# 绘制训练样本点
plt.scatter(X_train_pca[:, 0], X_train_pca[:, 1], c=y_train_pca, edgecolors='k', cmap=plt.cm.Paired)
plt.xlabel('PCA Component 1')
plt.ylabel('PCA Component 2')
plt.title('OneVsOne PCA_SVM Decision Boundary with Liner Kernal')
plt.show()
# 一对一高斯核函数分类
# 创建支持向量机模型
svm_pca = OneVsOneClassifier(SVC(kernel='rbf', C=0.45))
svm_pca.fit(X_train_pca, y_train_pca)
# 在测试集上进行预测
y_pred_pca = svm_pca.predict(X_test_pca)

# 分析预测结果
accuracy_pca = svm_pca.score(X_test_pca, y_test_pca)
print("预测准确率(降维后):", accuracy_pca)

# 可视化决策边界
x_min_pca, x_max_pca = X_pca[:, 0].min() - 0.5, X_pca[:, 0].max() + 1
y_min_pca, y_max_pca = X_pca[:, 1].min() - 0.5, X_pca[:, 1].max() + 1
h_pca = 0.02  # 步长
xx_pca, yy_pca = np.meshgrid(np.arange(x_min_pca, x_max_pca, h_pca), np.arange(y_min_pca, y_max_pca, h_pca))
Z_pca = svm_pca.predict(np.c_[xx_pca.ravel(), yy_pca.ravel()])
Z_pca = Z_pca.reshape(xx_pca.shape)
plt.contourf(xx_pca, yy_pca, Z_pca, cmap=plt.cm.Paired)

# 绘制训练样本点
plt.scatter(X_train_pca[:, 0], X_train_pca[:, 1], c=y_train_pca, edgecolors='k', cmap=plt.cm.Paired)
plt.xlabel('PCA Component 1')
plt.ylabel('PCA Component 2')
plt.title('OneVsOne PCA_SVM Decision Boundary with RBF Kernal')
plt.show()
# 一对多线性核函数分类
# 创建支持向量机模型
svm_pca = OneVsRestClassifier(SVC(kernel='linear', C=0.45))
svm_pca.fit(X_train_pca, y_train_pca)
# svm = OneVsRestClassifier(SVC(kernel='rbf', C=0.45))
# 在测试集上进行预测
y_pred_pca = svm_pca.predict(X_test_pca)

# 分析预测结果
accuracy_pca = svm_pca.score(X_test_pca, y_test_pca)
print("预测准确率(降维后):", accuracy_pca)

# 可视化决策边界
x_min_pca, x_max_pca = X_pca[:, 0].min() - 0.5, X_pca[:, 0].max() + 1
y_min_pca, y_max_pca = X_pca[:, 1].min() - 0.5, X_pca[:, 1].max() + 1
h_pca = 0.02  # 步长
xx_pca, yy_pca = np.meshgrid(np.arange(x_min_pca, x_max_pca, h_pca), np.arange(y_min_pca, y_max_pca, h_pca))
Z_pca = svm_pca.predict(np.c_[xx_pca.ravel(), yy_pca.ravel()])
Z_pca = Z_pca.reshape(xx_pca.shape)
plt.contourf(xx_pca, yy_pca, Z_pca, cmap=plt.cm.Paired)

# 绘制训练样本点
plt.scatter(X_train_pca[:, 0], X_train_pca[:, 1], c=y_train_pca, edgecolors='k', cmap=plt.cm.Paired)
plt.xlabel('PCA Component 1')
plt.ylabel('PCA Component 2')
plt.title('OneVsRest PCA_SVM Decision Boundary with Linear Kernal')
plt.show()
# 一对多高斯核函数分类
# 创建支持向量机模型
svm_pca = OneVsRestClassifier(SVC(kernel='rbf', C=0.45))
svm_pca.fit(X_train_pca, y_train_pca)
# 在测试集上进行预测
y_pred_pca = svm_pca.predict(X_test_pca)

# 分析预测结果
accuracy_pca = svm_pca.score(X_test_pca, y_test_pca)
print("预测准确率(降维后):", accuracy_pca)

# 可视化决策边界
x_min_pca, x_max_pca = X_pca[:, 0].min() - 0.5, X_pca[:, 0].max() + 1
y_min_pca, y_max_pca = X_pca[:, 1].min() - 0.5, X_pca[:, 1].max() + 1
h_pca = 0.02  # 步长
xx_pca, yy_pca = np.meshgrid(np.arange(x_min_pca, x_max_pca, h_pca), np.arange(y_min_pca, y_max_pca, h_pca))
Z_pca = svm_pca.predict(np.c_[xx_pca.ravel(), yy_pca.ravel()])
Z_pca = Z_pca.reshape(xx_pca.shape)
plt.contourf(xx_pca, yy_pca, Z_pca, cmap=plt.cm.Paired)

# 绘制训练样本点
plt.scatter(X_train_pca[:, 0], X_train_pca[:, 1], c=y_train_pca, edgecolors='k', cmap=plt.cm.Paired)
plt.xlabel('PCA Component 1')
plt.ylabel('PCA Component 2')
plt.title('OneVsRest PCA_SVM Decision Boundary with RBF Kernal')
plt.show()

九、总结

至此，我们对基于支持向量机的小麦种子分类有了较为全面的认识。尽管支持向量机是传统的机器学习技术，但在小麦种子分类中它依然展现出了非凡的能力。它或许没有一些新兴技术那般耀眼的光环，但它的稳定性和准确性在这个特定的应用场景下，就像一位默默坚守岗位的守护者。随着技术的不断发展，我们期待看到支持向量机与其他技术的融合，进一步提升小麦种子分类的效率和精度，为农业生产提供更有力的保障，确保每一粒小麦种子都能在合适的环境中茁壮成长，为全球的粮食安全贡献自己的力量。