分布类可视化图像：数据分布的多维解析工具

分布类可视化图像：数据分布的多维解析工具

在数据驱动决策的时代，理解数据的分布特征至关重要。近期，我运用 Python 及其相关库，深入探究了直方图、密度图、箱线图、小提琴图以及 QQ 图等分布类可视化图像，旨在挖掘数据背后隐藏的信息。

直方图：数据分布的直观快照

特点（优势）

直观呈现：通过将数据分组，以矩形高度直观展示每组频数，能让人迅速把握数据在各区间的分布情况，对数据的集中趋势和离散程度一目了然。例如，在分析不同年龄段人群的网购消费金额时，可快速知晓各年龄段消费金额的集中区间。
易于理解：其简单明了的图形结构，即便非专业的数据分析师也能轻松读懂，广泛适用于各类数据展示场景。

劣势

区间依赖性：区间划分（bins 设置）对图形呈现影响极大。不同的划分方式可能导致对数据分布的误判，区间过宽会掩盖细节，过窄则使图形琐碎，难以看出整体趋势。
缺乏连续性：它以离散区间展示数据，无法像密度图那样连续、平滑地呈现数据的概率分布，在精确分析数据分布形态时表现力欠佳。

应用场景

在电商领域，分析不同年龄段人群的网购消费金额分布。通过直方图，商家能精准把握不同年龄段消费者的消费习惯，为产品定位、营销策略制定提供有力依据。

实验过程及结果

利用 numpy 生成不同年龄段的消费金额模拟数据（服从不同分布），通过 pandas 整理成 DataFrame。使用 seaborn 的 histplot 函数绘制直方图，调整 bins 等参数优化图形。添加注释标注各年龄段平均消费金额。结果图清晰展示出不同年龄段消费金额的分布差异，如年轻人消费集中在某区间，而中老年人分布不同。
运行结果：

import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

# 设置matplotlib支持中文
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.size'] = 12  # 设置全局字体大小

# 生成数据
np.random.seed(42)
young_ages = np.random.normal(loc=25, scale=3, size=300)
middle_ages = np.random.normal(loc=45, scale=5, size=250)
old_ages = np.random.normal(loc=65, scale=4, size=200)

young_spending = np.random.exponential(scale=200, size=300)
middle_spending = np.random.exponential(scale=350, size=250)
old_spending = np.random.exponential(scale=150, size=200)

ages = np.concatenate([young_ages, middle_ages, old_ages])
spending = np.concatenate([young_spending, middle_spending, old_spending])
age_groups = np.repeat(['年轻人', '中年人', '老年人'], [300, 250, 200])

df = pd.DataFrame({
    '年龄': ages,
    '网购消费金额': spending,
    '年龄组': age_groups
})

# 绘制直方图
plt.figure(figsize=(12, 8))
# 使用更柔和的颜色调色板
sns.histplot(data=df, x='年龄', y='网购消费金额', hue='年龄组', multiple='stack', bins=30, kde=False, palette="Set2")

# 添加注释
young_mean_age = np.mean(young_ages)
young_mean_spending = np.mean(young_spending)
middle_mean_age = np.mean(middle_ages)
middle_mean_spending = np.mean(middle_spending)
old_mean_age = np.mean(old_ages)
old_mean_spending = np.mean(old_spending)

plt.annotate(f'年轻人平均年龄: {young_mean_age:.2f} 岁，平均消费: {young_mean_spending:.2f} 元',
             xy=(young_mean_age, young_mean_spending),
             xytext=(young_mean_age - 10, young_mean_spending + 50),  # 调整注释位置
             arrowprops=dict(facecolor='blue', shrink=0.05, width=2, headwidth=8),  # 调整箭头样式
             horizontalalignment='center')

plt.annotate(f'中年人平均年龄: {middle_mean_age:.2f} 岁，平均消费: {middle_mean_spending:.2f} 元',
             xy=(middle_mean_age, middle_mean_spending),
             xytext=(middle_mean_age - 10, middle_mean_spending + 50),
             arrowprops=dict(facecolor='green', shrink=0.05, width=2, headwidth=8),
             horizontalalignment='center')

plt.annotate(f'老年人平均年龄: {old_mean_age:.2f} 岁，平均消费: {old_mean_spending:.2f} 元',
             xy=(old_mean_age, old_mean_spending),
             xytext=(old_mean_age - 10, old_mean_spending + 50),
             arrowprops=dict(facecolor='orange', shrink=0.05, width=2, headwidth=8),
             horizontalalignment='center')

plt.title('不同年龄段人群的网购消费金额直方图')
plt.xlabel('年龄')
plt.ylabel('网购消费金额（元）')
plt.legend(title='年龄组', fontsize=12)  # 设置图例字体大小
plt.grid(True, linestyle='--', alpha=0.5)  # 设置网格线样式和透明度
plt.show()

密度图：数据分布的细腻笔触

特点（优势）

连续平滑：以平滑曲线展示数据的概率密度分布，细腻呈现数据的分布形状，如是否对称、峰值位置等，有助于深入分析数据的内在特征。
对比优势：在比较多组数据分布时，通过不同颜色或线型的曲线叠加，能清晰展现各组数据分布的差异与重叠部分，便于深入对比分析。

劣势

数值模糊：相比直方图，不能直接展示每个区间的具体频数，对于需快速获取数据具体分布数量的用户不够直观。
噪声敏感：处理含噪声数据时，平滑曲线可能过度拟合噪声，导致对真实数据分布的误判，需进行适当的数据预处理。

应用场景

在汽车行业，用于分析不同品牌汽车的油耗分布，帮助消费者和制造商了解各品牌油耗的集中趋势和分布宽窄，评估燃油经济性。

实验过程及结果
借助 numpy 生成不同品牌汽车油耗模拟数据，经 pandas 整理后，使用 seaborn 的 kdeplot 函数绘制密度图，设置填充、透明度等参数美化图形。添加注释标注各品牌平均油耗。结果图清晰呈现不同品牌汽车油耗的分布差异，便于比较各品牌在油耗方面的表现。
运行结果

import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

 设置matplotlib支持中文
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

#生成数据
np.random.seed(42)
brand_a_mpg = np.random.normal(loc=30, scale=3, size=400)
brand_b_mpg = np.random.normal(loc=25, scale=4, size=350)
brand_c_mpg = np.random.normal(loc=22, scale=2, size=300)

brands = np.repeat(['品牌 A', '品牌 B', '品牌 C'], [400, 350, 300])
mpg = np.concatenate([brand_a_mpg, brand_b_mpg, brand_c_mpg])

df = pd.DataFrame({
    '汽车品牌': brands,
    '油耗（MPG）': mpg
})

#绘制密度图
plt.figure(figsize=(12, 8))
sns.kdeplot(data=df, x='油耗（MPG）', hue='汽车品牌', fill=True, common_norm=False, alpha=0.5)

#添加注释
brand_a_mean_mpg = np.mean(brand_a_mpg)
brand_b_mean_mpg = np.mean(brand_b_mpg)
brand_c_mean_mpg = np.mean(brand_c_mpg)

#调整品牌A注释位置
plt.annotate(f'品牌 A 平均油耗: {brand_a_mean_mpg:.2f} MPG',
             xy=(brand_a_mean_mpg, 0),
             xytext=(brand_a_mean_mpg - 2, -0.02),
             arrowprops=dict(facecolor='red', shrink=0.05),
             horizontalalignment='center')

#调整品牌B注释位置
plt.annotate(f'品牌 B 平均油耗: {brand_b_mean_mpg:.2f} MPG',
             xy=(brand_b_mean_mpg, 0),
             xytext=(brand_b_mean_mpg - 2, -0.025),
             arrowprops=dict(facecolor='purple', shrink=0.05),
             horizontalalignment='center')

#调整品牌C注释位置
plt.annotate(f'品牌 C 平均油耗: {brand_c_mean_mpg:.2f} MPG',
             xy=(brand_c_mean_mpg, 0),
             xytext=(brand_c_mean_mpg - 2, -0.03),
             arrowprops=dict(facecolor='brown', shrink=0.05),
             horizontalalignment='center')

plt.title('不同品牌汽车的油耗密度图')
plt.xlabel('油耗（MPG）')
plt.ylabel('密度')
plt.legend(title='汽车品牌')
plt.grid(True)
plt.show()

箱线图：数据分布的关键信息洞察器

特点（优势）

信息集成：能同时展示数据的四分位数、中位数和异常值等关键信息，通过箱体、中位数线、须和异常点的组合，全面呈现数据的分布特征和离散程度。
稳健性强：主要基于数据的分位数，对极端值（异常值）不敏感，能在存在异常值的情况下，依然有效展示数据的主体分布情况。

劣势

细节缺失：相较于直方图和密度图，无法详细展示数据在各个区间的具体分布情况，对于深入了解数据细节分布的场景，提供的信息有限。
复杂分布难显：当数据分布较为复杂，尤其是多峰分布时，难以像密度图那样清晰展示分布的多个峰值和具体形态，不利于全面理解复杂分布。
应用场景
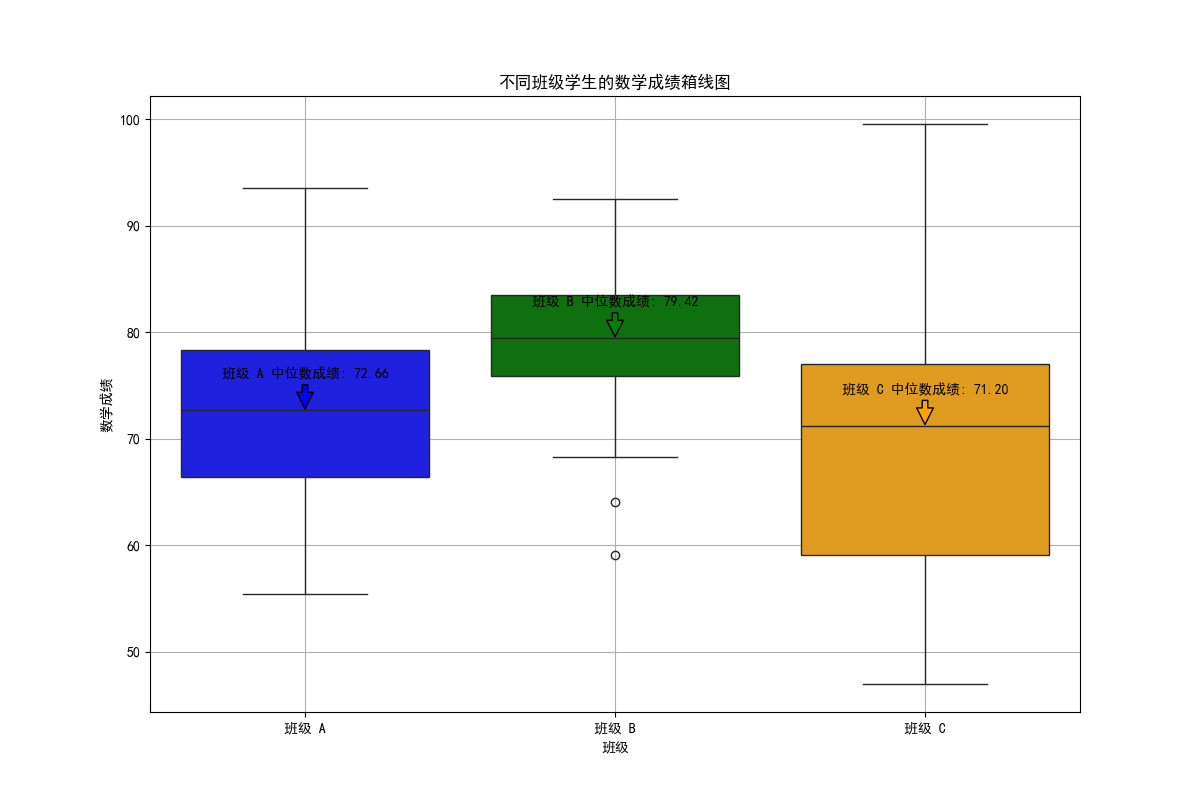
在教育领域，比较不同班级学生的数学考试成绩。箱线图可直观展示各班成绩的中位数、离散程度及异常值，助力教师和教育管理者评估班级间成绩差异，针对性调整教学策略。
实验过程及结果
用 numpy 生成不同班级学生成绩模拟数据并整理成 DataFrame，调用 seaborn 的 boxplot 函数绘制箱线图，设置颜色调色板区分不同班级。添加注释标注各班中位数成绩。结果图清晰呈现不同班级成绩的分布特征，便于比较各班成绩差异。
运行结果：

import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

# 设置 matplotlib 支持中文
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 生成数据
np.random.seed(42)
class_a_scores = np.random.normal(loc=75, scale=10, size=50)
class_b_scores = np.random.normal(loc=80, scale=8, size=55)
class_c_scores = np.random.normal(loc=70, scale=12, size=45)

classes = np.repeat(['班级 A', '班级 B', '班级 C'], [50, 55, 45])
scores = np.concatenate([class_a_scores, class_b_scores, class_c_scores])

df = pd.DataFrame({
    '班级': classes,
    '数学成绩': scores
})

# 绘制箱线图
plt.figure(figsize=(12, 8))
sns.boxplot(data=df, x='班级', y='数学成绩', palette=['blue', 'green', 'orange'])

# 添加注释
class_a_median = np.median(class_a_scores)
class_b_median = np.median(class_b_scores)
class_c_median = np.median(class_c_scores)

plt.annotate(f'班级 A 中位数成绩: {class_a_median:.2f}',
             xy=(0, class_a_median),
             xytext=(0, class_a_median + 3),
             arrowprops=dict(facecolor='blue', shrink=0.05),
             horizontalalignment='center')

plt.annotate(f'班级 B 中位数成绩: {class_b_median:.2f}',
             xy=(1, class_b_median),
             xytext=(1, class_b_median + 3),
             arrowprops=dict(facecolor='green', shrink=0.05),
             horizontalalignment='center')

plt.annotate(f'班级 C 中位数成绩: {class_c_median:.2f}',
             xy=(2, class_c_median),
             xytext=(2, class_c_median + 3),
             arrowprops=dict(facecolor='orange', shrink=0.05),
             horizontalalignment='center')

plt.title('不同班级学生的数学成绩箱线图')
plt.xlabel('班级')
plt.ylabel('数学成绩')
plt.grid(True)
plt.show()

小提琴图：数据分布的融合之美

特点（优势）

优势融合：巧妙融合箱线图和密度图的优点，既展示数据的分布形状，又呈现数据的四分位数等信息，从多个角度全面呈现数据分布特征。
视觉吸引力：独特的图形形状使其在展示数据时更具吸引力，能在直观呈现数据分布的同时，给人良好的视觉体验，适用于报告和展示。

劣势

解读门槛：由于融合多种信息，对于不熟悉该图表的人来说，解读可能需要一定时间和专业知识，不如简单图表容易理解。
绘制成本：相比简单图表，小提琴图的绘制需要更多计算资源和代码设置，在处理大规模数据或对效率要求高的场景中存在局限性。
应用场景
在宠物饲养领域，研究不同种类宠物的体重分布。小提琴图可清晰比较狗、猫、兔子等宠物的体重分布情况，为饲养者在选择宠物、安排饮食和生活空间等方面提供指导。
实验过程及结果
利用 numpy 生成不同宠物种类体重模拟数据，经 pandas 整理后，使用 seaborn 的 violinplot 函数绘制小提琴图，设置不同颜色区分宠物种类。添加注释标注各宠物种类中位数体重。结果图直观展示不同宠物种类体重分布差异，方便比较。
运行结果：

import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

# 设置matplotlib支持中文
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 生成数据
np.random.seed(42)
dog_weights = np.random.normal(loc=15, scale=3, size=30)
cat_weights = np.random.normal(loc=5, scale=1, size=40)
rabbit_weights = np.random.normal(loc=2, scale=0.5, size=35)

pet_types = np.repeat(['狗', '猫', '兔子'], [30, 40, 35])
weights = np.concatenate([dog_weights, cat_weights, rabbit_weights])

df = pd.DataFrame({
    '宠物种类': pet_types,
    '体重（千克）': weights
})

# 绘制小提琴图
plt.figure(figsize=(12, 8))
ax = sns.violinplot(data=df, x='宠物种类', y='体重（千克）', palette=['red', 'purple', 'brown'])

# 添加注释
dog_median = np.median(dog_weights)
cat_median = np.median(cat_weights)
rabbit_median = np.median(rabbit_weights)

# 调整狗的注释位置并增大字体
plt.annotate(f'狗的中位数体重: {dog_median:.2f} 千克',
             xy=(0, dog_median),
             xytext=(0, dog_median + 3),
             arrowprops=dict(facecolor='red', shrink=0.05),
             horizontalalignment='center',
             fontsize=12)

# 调整猫的注释位置并增大字体
plt.annotate(f'猫的中位数体重: {cat_median:.2f} 千克',
             xy=(1, cat_median),
             xytext=(1, cat_median + 2),
             arrowprops=dict(facecolor='purple', shrink=0.05),
             horizontalalignment='center',
             fontsize=12)

# 调整兔子的注释位置并增大字体
plt.annotate(f'兔子的中位数体重: {rabbit_median:.2f} 千克',
             xy=(2, rabbit_median),
             xytext=(2, rabbit_median + 1.5),
             arrowprops=dict(facecolor='brown', shrink=0.05),
             horizontalalignment='center',
             fontsize=12)

plt.title('不同种类宠物的体重小提琴图')
plt.xlabel('宠物种类')
plt.ylabel('体重（千克）')
plt.grid(True)
plt.show()

QQ 图：数据分布的正态性检验利器

特点（优势）

正态性判断：专门用于检验数据是否服从正态分布，通过观察样本分位数与理论分位数的对应关系，直观判断数据与正态分布的拟合程度，为数据的统计分析提供重要依据。
异常值突显：在检验正态性过程中，能有效检测出数据中的异常值，因为异常值会明显偏离直线，便于及时发现数据中的特殊情况。

劣势

功能局限：主要专注于检验正态分布，对于其他类型的数据分布分析，如偏态分布、多峰分布等，无法提供有效信息，应用场景相对狭窄。
分布展示不足：不像其他图表那样能直观展示数据的具体分布情况，如频数、概率密度等，对于只想快速了解数据分布大致形态的用户帮助不大。
应用场景
在电池制造行业，检验不同型号电池的续航时间是否符合正态分布，帮助工程师和质量控制人员评估产品质量稳定性，排查生产过程中的潜在问题。
实验过程及结果
使用 numpy 生成不同型号电池续航时间模拟数据并整理，借助 scipy 库的 stats.probplot 函数针对每个型号分别绘制 QQ 图，添加注释标注中位数续航时间。结果图直观呈现各型号电池续航时间与正态分布的拟合情况，便于评估产品质量。
运行结果：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats

# 设置matplotlib支持中文
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 生成数据
np.random.seed(42)
model_a_battery = np.random.normal(loc=20, scale=2, size=50)
model_b_battery = np.random.normal(loc=18, scale=3, size=45)
model_c_battery = np.random.normal(loc=22, scale=1.5, size=55)

models = np.repeat(['型号 A', '型号 B', '型号 C'], [50, 45, 55])
battery_life = np.concatenate([model_a_battery, model_b_battery, model_c_battery])

df = pd.DataFrame({
    '电池型号': models,
    '续航时间（小时）': battery_life
})

# 分别绘制QQ图
models_list = ['型号 A', '型号 B', '型号 C']
colors = ['blue', 'green', 'orange']

for i, model in enumerate(models_list):
    model_data = df[df['电池型号'] == model]['续航时间（小时）']
    median = np.median(model_data)

    plt.figure(figsize=(8, 6))
    stats.probplot(model_data, dist="norm", plot=plt)
    plt.title(f'{model} 电池续航时间的 QQ 图')
    plt.xlabel('理论分位数')
    plt.ylabel('样本分位数')

    # 添加注释
    plt.annotate(f'中位数续航时间: {median:.2f} 小时',
                 xy=(0, median),
                 xytext=(0.2, median + 1),  # 调整注释位置
                 arrowprops=dict(facecolor=colors[i], shrink=0.05),
                 horizontalalignment='left',
                 fontsize=10)  # 设置字体大小

    plt.tight_layout()
    plt.show()

图表类型	优势	劣势	本文的应用场景	本文的实验过程及结果
直方图	直观展示数据区间频数，易于理解	区间划分影响大，缺乏连续性	电商领域分析不同年龄段网购消费金额分布	利用 numpy、pandas、seaborn 生成、整理数据并绘制，展示不同年龄段消费金额分布差异
密度图	连续平滑展示数据分布，便于对比	缺乏具体数值信息，易受噪声影响	汽车行业分析不同品牌汽车油耗分布	借助相关库生成、整理数据并绘制，呈现不同品牌油耗分布差异
箱线图	展示关键分位信息，抗干扰性强	细节展示不足，难比较复杂分布	教育领域比较不同班级学生数学成绩	用相关库生成、整理数据并绘制，呈现不同班级成绩分布特征及差异
小提琴图	融合多种优势，视觉效果好	解读难度稍高，绘制成本较高	宠物饲养领域研究不同宠物体重分布	利用相关库生成、整理数据并绘制，直观展示不同宠物体重分布差异
QQ 图	有效检验正态分布，能检测异常值	功能单一，缺乏直观分布展示	电池制造行业检验电池续航时间正态性	使用相关库生成、整理数据并绘制，呈现各型号电池续航时间与正态分布拟合情况