MATLAB实现相机标定

山茶花阁下

已于 2024-11-15 14:34:15 修改

阅读量3.8k

点赞数 26

文章标签：数码相机 matlab 计算机视觉相机

于 2024-11-09 15:00:34 首次发布

本文链接：https://blog.csdn.net/pumpkinn233/article/details/143644092

版权

张友定标定法：

相机标定的目标是求出相机的内参、外参和畸变系数。这三个部分可以描述相机成像的过程：
内参：描述相机的光学特性，例如焦距和图像中心位置。
外参：描述相机相对于世界坐标系的位置和方向。
畸变系数：描述镜头的光学畸变。
公式如下:
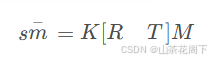
在这里插入图片描述
其表示三维世界点 M 投影到二维图像平面上的过程。
s：一个尺度因子，用于表示从世界坐标到图像坐标的缩放比例。
𝑚：图像平面上的坐标（像素坐标），即三维点在图像中的位置。
𝐾：相机的内参矩阵，具体为：
在这里插入图片描述
fx和fy：表示相机的焦距（在 x 和 y 方向的像素单位）
cx和cy：表示图像的中心点（主点）的像素坐标。
[RT]：相机的外参矩阵，其中包含旋转矩阵
R 和平移向量
T，描述相机相对于世界坐标系的位置和方向。
R 是一个 3x3 的旋转矩阵，表示相机坐标系相对于世界坐标系的旋转。
T 是一个 3x1 的平移向量，表示相机坐标系相对于世界坐标系的位移。
M：三维世界坐标系下的点（也称为世界坐标点），通常表示为 (X,Y,Z)。
张正友标定方法的核心即是采用平面标定板，从而可以方便的将标定点的真值Z置为0，以此方便计算。

代码解析：

棋盘格参数定义：

checkerboardSquareSize = 21.25; %每个小方格的实际物理尺寸（mm）
numSquaresX = 7; % 棋盘格在 X 方向的内角点数（列数 - 1）
numSquaresY = 10; % 棋盘格在 Y 方向的内角点数（行数 - 1）

设置棋盘格的实际尺寸（方块边长）和角点数量，用于确定棋盘格的物理世界坐标。

棋盘格角点检测

imageFileNames = fullfile(imageFolder, {imageFiles.name});
[imagePoints, boardSize, imagesUsed] = detectCheckerboardPoints(imageFileNames);

使用 detectCheckerboardPoints 函数检测每张图像中的棋盘格角点。
imagePoints 保存角点的像素坐标，boardSize 为棋盘格尺寸，imagesUsed 标记成功检测到棋盘格的图像。

去除未检测到棋盘格的图像

imageFileNames = imageFileNames(imagesUsed);

过滤掉那些未成功检测到棋盘格角点的图像文件，确保后续操作只使用检测成功的图像。

设置棋盘格的世界坐标

worldPoints = generateCheckerboardPoints(boardSize, checkerboardSquareSize);

根据棋盘格的物理尺寸，生成实际的三维世界坐标 worldPoints。这些坐标用于建立世界坐标与图像坐标之间的映射关系。

相机参数估计

cameraParams = estimateCameraParameters(imagePoints, worldPoints);

estimateCameraParameters 函数通过最小化重投影误差来计算相机的内参矩阵、畸变参数和标定误差。
常用调用方法：[cameraParams, imagesUsed, estimationErrors] = estimateCameraParameters(imagePoints, worldPoints);

重投影误差定义为：从世界坐标投影到图像坐标系的点，与实际检测到的图像坐标之间的差距（误差越小，标定越准确）。

输出标定结果

% 显示相机内参矩阵 K
fx = cameraParams.FocalLength(1);  % 焦距 fx
fy = cameraParams.FocalLength(2);  % 焦距 fy
cx = cameraParams.PrincipalPoint(1);  % 主点 cx
cy = cameraParams.PrincipalPoint(2);  % 主点 cy

K = [fx, 0, cx;
     0, fy, cy;
     0,  0,  1];

disp('相机内参矩阵 K：');
disp(K);

% 显示畸变系数
disp('畸变系数:');
disp(cameraParams.RadialDistortion);

% 显示误差均方根（RMSE）
disp('误差均方根（RMSE）：');
disp(cameraParams.MeanReprojectionError);

显示计算得到的内参矩阵、径向畸变参数和均方根误差（RMSE），以评估标定的准确性。

显示重投影误差

figure;
showReprojectionErrors(cameraParams);
title('重投影误差');

showReprojectionErrors 函数生成重投影误差图，用于评估每张图像的标定误差。

可视化标定结果

figure;
imshow(imageFileNames{1});
hold on;
plot(imagePoints(:,1,1), imagePoints(:,2,1), 'go');
hold off;
title('标定结果');

显示第一个图像，并在其上绘制检测到的棋盘格角点，以可视化检测效果。

标定过程：

拍摄多张不同角度的棋盘格照片
在这里插入图片描述
这里是直接用显示器棋盘格照片进行拍摄

角点检测
在这里插入图片描述
输出标定结果

输出的相机内参矩阵为：在这里插入图片描述
相机内参矩阵 K：

焦距：1581.9 和 1583.3 分别是相机在 X 和 Y 方向的焦距（单位：像素）。
这表示相机的成像比例在 X 和 Y 方向上基本一致。
主点：1017.3 和 1029.6 是图像平面上主点的像素坐标。
主点坐标即相机光轴与图像平面的交点，通常接近图像中心，但实际拍摄中可能会略微偏离。
尺度因子：最后一行的 [0, 0, 1] 表示齐次坐标，通常用于标准化坐标转换。
在这里插入图片描述

显示的畸变系数为：

径向畸变系数：-0.1628
切向畸变系数：0.1335

畸变系数解释：
径向畸变：-0.1628 表示图像存在轻微的径向畸变，通常导致“桶形”或“枕形”变形。
畸变值越大，图像边缘的变形越明显。该数值相对较小，表明畸变较轻。
切向畸变：0.1335 表示切向畸变程度。
切向畸变是由于镜头和图像传感器不完全平行，导致图像出现轻微倾斜。

重投影误差均方根（RMSE）
输出的 RMSE 为：
RMSE=0.3675

RMSE（Root Mean Square Error）表示标定精度，数值越小说明标定越精确。
0.3675 像素的 RMSE 表示重投影误差相对较小，说明标定过程相对精确。
RMSE 表示在标定过程中，计算的角点位置与实际检测位置之间的平均误差（单位：像素）。通常 RMSE 小于 1 像素就表示标定精度较好。

相机标定的重投影误差
在这里插入图片描述
该图显示了相机标定的重投影误差（Reprojection Error），每个柱状条表示一张标定图像的平均重投影误差。以下是详细分析：
纵轴（Mean Error in Pixels）：
表示重投影误差的平均值，单位为像素。
误差越小，说明标定结果越精确。
横轴（Images）：
表示用于标定的每一张图像编号，从 1 到 8，对应不同的标定图像。
蓝色柱状条：
每个柱状条表示一张标定图像的重投影误差（均值）。
重投影误差是指图像上实际检测到的角点位置与根据标定参数重新投影得到的角点位置之间的差距。
数值越小，说明该图像对于标定的误差越小，标定的精度越高。
虚线（Overall Mean Error）：
图中的虚线表示总体平均重投影误差，标记为 0.37 pixels。虚线的位置表示所有图像的重投影误差的平均值。这是一个评估标定总体精度的重要指标。
图中关键点分析
大多数图像的误差集中在 0.2 到 0.5 像素范围内：这说明标定过程中，大多数图像的重投影误差较小，标定效果较为理想。
第 8 张图像的误差最高：第 8 张图像的平均重投影误差接近 0.8 像素，比其他图像的误差高出不少。可能的原因包括：角点检测受干扰、图像拍摄角度问题、光照条件变化，或棋盘格在该图像中存在畸变。这可能降低了该图像对标定精度的贡献。
第 1 张和第 6 张图像的误差较低：这些图像的重投影误差接近 0.2 像素，说明它们的标定效果非常好，有助于提升整体标定精度。