动态规划（机器人移动问题）

  动态规划最核心的思想，就在于拆分子问题，记住过往，减少重复计算。

  子问题重叠 : 即是当使用递归进行自顶向下的求解时,每次产生的子问题不总是新的问题,而是已经被重复计算过的问题.动态规划利用了这种性质,使用一个集合将已经计算过的结果放入其中,当再次遇见重复的问题时,只需要从集合中取出对应的结果.

  可以通过一个机器人移动问题来了解动态规划；

  问题要求如下：

1.假设有排成一行的n个位置记为1-N,N一定大于等于2
2.开始时机器人在m位置上，m一定是1-N中的一个
3.机器人要在规定的步数到达指定的终点，计算到达指定终点的路线有多少条
4.如果机器人来到1位置只能往右来到2位置
5.如果机器人来到N位置只能往左来到N-1位置
6.如果机器人在其他位置，则机器人可以往右也可以往左

  首先根据问题，我们很容易想到可以通过递归来实现，因此我们写下一个无任何优化的递归实现的代码：

  

//普通未优化版本

int RobotMove1(int start,int move,int aim,int N)      // start代表起始位置(当前位置)，move代表移动步数，aim代表目标位置，N代表移动范围从1-N;
{
	if (0== move)      //移动步数为0已经不能移动了
	{
		return start == aim ? 1 : 0;
	}

	else if (1 == start)
	{
		return RobotMove1(2, move - 1, aim, N);
	}

	else if (N == start)
	{
		return RobotMove1(N-1, move - 1, aim, N);
	}

	else
	{
		return RobotMove1(start - 1, move - 1, aim, N) + RobotMove1(start + 1, move - 1, aim, N);
	}
}

  这个递归函数传入的参数中aim和N是永远不会变的，所以函数返回的值只与start和move的数值有关

  我们会发现这个递归过程中有着重复的过程，比如此时我们要从4位置走6步到6位置，此时走的路线便是如下图所示的路线：

  

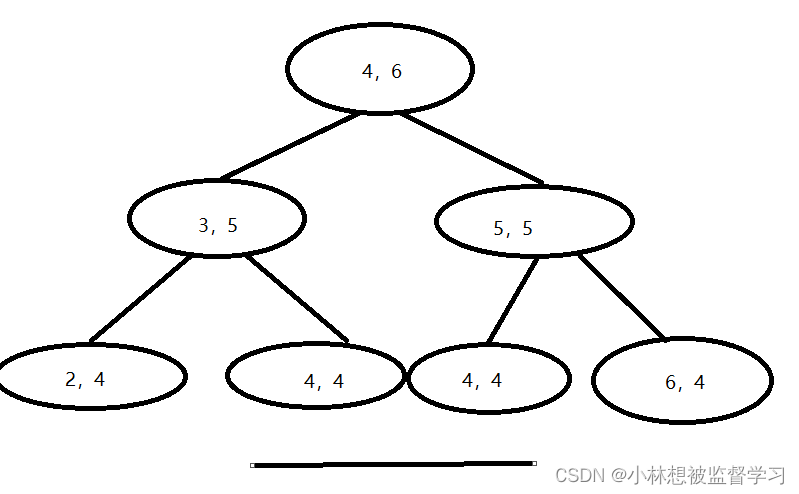
 我们从4位置走到3或者5位置后还剩5步，从3位置走到2或者4位置还剩4步，按这个规律可以画出部分过程的图示，在图中下划线的地方，我们发现有同样的数据

  这就说明每次产生的子问题不总是新的问题,而是已经被重复计算过的问题，所以我们就可以通过动态规划来对这个程序进行优化。

---

  于是我们考虑生成一个数组来储存每次发生过的过程，当这个过程再次发生的时候我们便可以在数组中直接获得这个过程的结果，这样会节省大量的时间。

  根据这个想法，我们写出了优化一版本（加入动态规划，以空间换时间）

  代码如下：

int RobotMethod2(int start, int move, int aim, int N, int* arr)
{
	int ans = 0;      //用来储存路线条数的变量
	if (-1 != arr[start * N + move])      //以前经历过相同的步骤
	{
		return arr[start * N + move];
	}

	else if (0 == move)      //以前没有经历过相同的步骤
	{
		ans = start == aim ? 1 : 0;
	}

	else if (1 == start)
	{
		ans = RobotMethod2(2, move - 1, aim, N, arr);
	}

	else if (N == start)
	{
		ans = RobotMethod2(N-1, move - 1, aim, N, arr);
	}

	else
	{
		ans = RobotMethod2(start - 1, move - 1, aim, N, arr) + RobotMethod2(start + 1, move - 1, aim, N, arr);
	}

	arr[start * N + move] = ans;
	return ans;
}

int RobotMove2(int start, int move, int aim, int N)      //arr代表二维数组，当arr数组中的值为-1时代表之前没有过该步骤
{
	int* arr = new int[(N + 1) * (move + 1)];      //开辟一维数组的空间表示二维数组,行是 start，列是move
	for (int i = 0; i < (N + 1) * (move + 1); i++)
	{
		arr[i] = -1;
	}
	return RobotMethod2(start, move, aim, N, arr);
}

    我们创建一个二维数组arr，行坐标表示start，列坐标表示move，将内容初始化为-1，我们在进行递归之前都先判断一下arr【start】【move】中有没有存放数据，要是存放了非-1的数据就说明之前我们已经经历过了在start这个位置，移动步数剩余move的这个过程，直接将结果取出来用就行了。

  有取当然也有存，我们在递归的过程中要将当前在start这个位置，移动步数剩余move的路线条数存入arr数组。也就是将该过程的结果存入arr【start】【move】

---

  我们的这个代码还可以进行最后的优化，这样才算是最正宗的动态规划，我们可以根据递归与数组之间的联系，直接将各种情况的结果填入数组中，代码如下：

//优化二版本（最终版，无递归，只有迭代和空间的使用）(正宗的动态规划)
//编写思路是根据递归找到规律，直接根据规律填开辟的空间

int RobotMethod3(int start, int move, int aim, int N, int** arr)    // start代表起始位置(当前位置)，move代表移动步数，aim代表目标位置，N代表移动范围从1-N;
{
	//当move为0时除了到达aim位置为1，其余位置都为0
	//根据ans = start == aim ? 1 : 0;
	for (int i = 1; i <= N; i++)
	{
		arr[i][0] = 0;
	}
	arr[aim][0] = 1;


	for (int j = 1; j <= move; j++)
	{
		//根据ans = RobotMethod2(2, move - 1, aim, N, arr)
		arr[1][j] = arr[2][j - 1];

		//根据ans = RobotMethod2(start - 1, move - 1, aim, N, arr) + RobotMethod2(start + 1, move - 1, aim, N, arr);
		for (int i = 2; i <= N - 1; i++)
		{
			arr[i][j] = arr[i - 1][j - 1] + arr[i + 1][j - 1];
		}

		//根据ans = RobotMethod2(N-1, move - 1, aim, N, arr);
		arr[N][j] = arr[N - 1][j - 1];
	}

	return arr[start][move];
}

int RobotMove3(int start, int move, int aim, int N)      //arr代表二维数组，当arr数组中的值为-1时代表之前没有过该步骤
{
	//开辟二维数组arr的空间
	int** arr = new int* [N + 1];
	for (int j = 0; j <= move; j++)
	{
		arr[j] = new int[move + 1];
	}
	return RobotMethod3(start, move, aim, N, arr);
}

  1.根据我们一开始的递归代码

if (0== move)      //移动步数为0已经不能移动了
    {
        return start == aim ? 1 : 0;
    }

  我们知道当move为0时只有start == aim的情况路线数为1，其余都为0，所以我们可以得到在数组arr中的move=0时，只有arr【aim】【move】为1其余的都为0，于是我们可以直接对数组arr进行如下的处理：

for (int i = 1; i <= N; i++)
	{
		arr[i][0] = 0;
	}
	arr[aim][0] = 1;

  2.根据

else if (1 == start)
	{
		ans = RobotMethod2(2, move - 1, aim, N, arr);
	}

	else if (N == start)
	{
		ans = RobotMethod2(N-1, move - 1, aim, N, arr);
	}

	else
	{
		ans = RobotMethod2(start - 1, move - 1, aim, N, arr) + RobotMethod2(start + 1, move - 1, aim, N, arr);
	}

  我们知道当start为1时，路线数和start为2，移动步数减1后的路线数完全相同。

  同理当start为N时，路线数和start为N-1，移动步数减1后的路线数完全相同。

  当start为2---N-1时，路线数是start为start - 1，移动步数减1后的路线数加上start为start + 1，移动步数减1后的路线数

  所以我们可以直接对数组进行如下的处理：

for (int j = 1; j <= move; j++)
	{
		//根据ans = RobotMethod2(2, move - 1, aim, N, arr)
		arr[1][j] = arr[2][j - 1];

		//根据ans = RobotMethod2(start - 1, move - 1, aim, N, arr) + RobotMethod2(start + 1, move - 1, aim, N, arr);
		for (int i = 2; i <= N - 1; i++)
		{
			arr[i][j] = arr[i - 1][j - 1] + arr[i + 1][j - 1];
		}

		//根据ans = RobotMethod2(N-1, move - 1, aim, N, arr);
		arr[N][j] = arr[N - 1][j - 1];
	}

  于是就得到了我们最终去除递归，采用动态规划的版本。