本系列为斯坦福 Dan Boneh教授的"密码学 I"的学习笔记
课程网址: http://www.coursera.org/lecture/crypto/course-overview-lboqg
内容在CSDN、知乎和微信公众号同步更新

- Markdown源文件暂未开源,如有需要可联系邮箱
- 笔记难免存在问题,欢迎联系邮箱指正
课程完整目录如下
- 课程大纲
- 0 Introduction
- 1 Stream Ciphers
- 2 Block Ciphers
- 3 Message Integrity
- 4 Authenticated Encryption
- 5 Basic Key Exchange
- 6 Public-Encryption
本文为其中Chapter 6 Public-Encryption 的内容,包括:
文章目录
- 6 Public-Encryption
- 6.1 Public Key Encryption from Trapdoor Permutations
- 6.2 Public Key Encryption from Trapdoor Permutations: RSA
- 6.3 Public Key Encryption from Trapdoor Permutations: Attacks
- 6.4 Public Key Encryption From Diffie-Hellman: EIGamal
- 6.5 Public Key Encryption: Summary
6 Public-Encryption
6.1 Public Key Encryption from Trapdoor Permutations
Trapdoor Permutations 陷门置换
This chapter:
- constuct a number of secure public key encryption schemes
6.1.1 Definitions and Security
首先:
- 定义what is public key encryption
- 以及the security of public key!
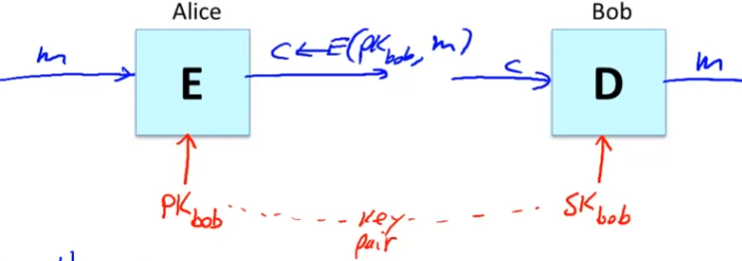
Public key encryption
- Bob
- generates (Pk, SK) and gives PK to Alice
- Pk and SK:
- key pair
Applicaions
公钥加密 (public key encryption)两大应用:
- Session setup
- non-interact encryption
此外, public key 还可以用于认证
- Session setup
- 建立会话密钥x
- for now, 只讲了only eavestrdopping security

- Non-interactive applications:
- e.g., Email
- 通信双方无法即时通信
- 无法establish session key
- Note: Bob needs
p
k
a
l
i
c
e
pk_{alice}
pkalice
- 通过public key management实现
- e.g., Email
Public key encryption
- Def: a public-key encryption system is a triple of algs (G,E,D)
- G(): randomized alg. outputs a key pair (pk, sk)
- E(pk, m): randomized alg. that taks
m
∈
M
m\in M
m∈M
- outputs c ∈ C c \in C c∈C
- D(sk,c): det. alg. that takes c ∈ C c \in C c∈C and outputs m ∈ M m\in M m∈M or ⊥ \perp ⊥
- Consistency:
-
∀
(
p
k
,
s
k
)
\forall (pk,sk)
∀(pk,sk) output by G:
- ∀ m ∈ M \forall m \in M ∀m∈M: D(sk, E(pk, m)) = m
-
∀
(
p
k
,
s
k
)
\forall (pk,sk)
∀(pk,sk) output by G:
Semantci Security (as a quick review)
- For b = 0,1 define experiments EXP(0) and EXP(1) as:
- 1st: the challenger run the key generation alg.
- 2nd: the challenger send pk to the adv.
- and keep the sk to himself
- 3rd: the adv output two equal length messages: m 0 m_0 m0 and m 1 m_1 m1
- 4th: the challenger 任选 m 0 m_0 m0 / m 1 m_1 m1之一进行加密,并返回 c ← E ( p k , m b ) c \leftarrow E(pk,m_b) c←E(pk,mb)
- 5th: the adv. 猜测b的值,若猜对则攻击成功
- Semantic security definition:
- 目标:攻击者无法区分到底是实验0还是实验1,即输出0和输出1的概率是相等:
- Def: E= (G,E,D) is sem. secure (a.k.a IND-CPA)
- INDistinguishability under Chosen Plaintext Attack
- if for all efficient A:
- A d v S S [ A , E ] = ∣ P r [ E X P ( 0 ) = 1 ] − P r [ E X P ( 1 ) = 1 ] ∣ < n e g l i g i b l e Adv_{SS}[A,E] = |Pr[EXP(0)=1] - Pr[EXP(1)=1]| < negligible AdvSS[A,E]=∣Pr[EXP(0)=1]−Pr[EXP(1)=1]∣<negligible
- 注意:
- 对于public encryption, 没有必要突出“选择明文攻击”
- The adv. 根据pk可自行Encryption, 因为没有区分"选择明文"攻击
- 该定义仅适用于概率性加密方案,即仅根据E和pk无法得到唯一的encryption + 敌手必须是多项式时间
- 否则敌手就可以计算出encryption再进行比较
- (来自杨波老师现代密码学第四版):
- 对于public encryption, 没有必要突出“选择明文攻击”
Relation to symmetric cipher security
-
Recall: for symmetric ciphers we had two security notions:
One-time securityandmany-time security- One-time security: Key used once
- many-time security: Key used many times
- We showed that one-time security 弱于 many-time security
-
For public key encryption
- One-time security 和 many-time security (CPA) 等价!!
- follows from the fact that attacker can decrypt by himself!
- adv.能够自行使用pk加密任意多的消息!
- One-time security 和 many-time security (CPA) 等价!!
-
结论:
- public key 本质上 inherently 就是和加密many messages using one given public key!
- 不需要经常更换密钥
- public key 本质上 inherently 就是和加密many messages using one given public key!
Security against active attacks
主动攻击
- CCA Security!
- Authenticated Encryption!
- What if attacker can tampler with ciphertext?
- 一个gmail的例子
- attacker通过更改header 实现攻击
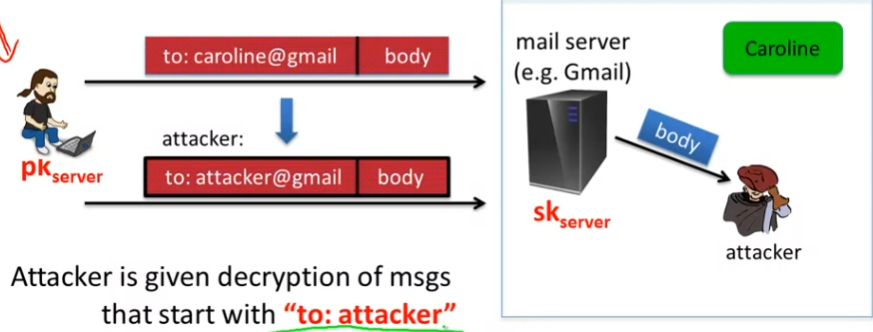
- 如何抵御主动攻击?
- 首先要引入CCA的definition
(pub-key) Chosen Ciphertext Security: definition
-
E = (G,E,D) public-key enc. over (M,C)
-
For b = 0,1 define EXP(b)
- 1st: 定义exp 0 和 exp 1
- 2nd: Chal. generates (pk,sk)
- 3rd: send pk to the adv.
- 4th: CCA phase 1:
- 5th: Adv. 选择挑战消息 m 0 m_0 m0 和 m 1 m_1 m1, 发给 challenger
- 6th: 挑战者返回某实验下的c
- 7th: adv. 再次选择一个密文,该密文只要和6th中的c不同即可
- 并得到相应的明文
- 最后,adv. 根据以上所有的信息去判断b, 只要能判断出b, 就不安全
-
整个过程:
- T**he adv. 能够获得任何ciphertext的decryption**
- 除了 challenge ciphertext c
- 即便Adv. 获得这么多解密的消息
- 它也无法判断challenge plaintext 到底是 $ m 1 m_1 m1 还是 m 0 m_0 m0
- 所以其实是一个非常保守的定义
- 比上一页定义的攻击更加保守!
- T**he adv. 能够获得任何ciphertext的decryption**
-
Def: E is CCA secure (a.k.a IND-CCA) if for all efficient A:
- A d v C C A [ A , E ] = ∣ P r [ E X P ( 0 ) = 1 ] − P r [ E X P ( 1 ) = 1 ] ∣ i s n e g l i g i b l e Adv_{CCA}[A,E] = |Pr[EXP(0) = 1] - Pr[EXP(1) = 1]| is negligible AdvCCA[A,E]=∣Pr[EXP(0)=1]−Pr[EXP(1)=1]∣isnegligible
-
Example:
- 刚刚gmali攻击的例子
- Suppose (to: Alice, body) → \rightarrow → (to: charlie, body)
- 被攻击的本质原因:
- The adv. 拥有完成从 E(to:alice, b) 到 E(to:charlie, b)的能力!
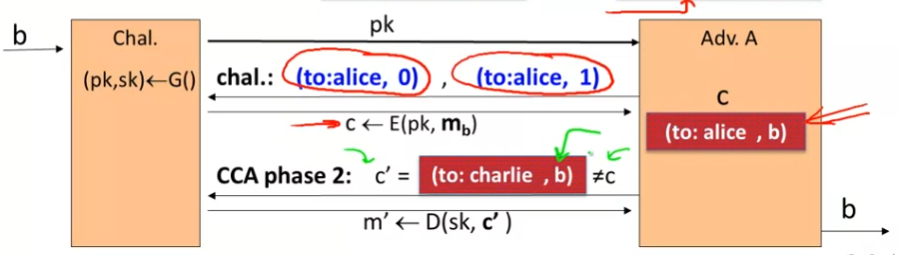
- 可见, Adv.能够轻易地从CCA phase 2中获得b
Public-key CCA security的神奇之处:
- 即便the attacker有能力decrypt除了challenge ciphertext外的任何密文,它也就是没办法decrypt challenge ciphertext!
This and next module:
- Constructing CCA secure pub-key systems
- 每次不是CCA secure 的public key systems都会出现安全问题
6.1.2 Constructions
Last segment:
- What a pubic key encryption system is
- What it means for a public key encrypion system to be secure
- defined CCA security
This segment:
- start by constructing public key encryptions from
trapdoor permutation
Trapdoor functions (TDF)
-
Def: a trapdoor func. X → Y X\rightarrow Y X→Y is a triple of efficient algs. (G, F, F − 1 F^{-1} F−1)
- G(): randomized alg. outputs a key pair (pk,sk)
- 产生密钥对
- F(pk, ⋅ \cdot ⋅): det. alg. that defines a function X → Y X \rightarrow Y X→Y
- F − 1 ( s k , ⋅ ) F^{-1}(sk,\cdot) F−1(sk,⋅): defines a function Y → X Y\rightarrow X Y→X that inverts F ( p k , ⋅ ) F(pk, \cdot) F(pk,⋅)
- G(): randomized alg. outputs a key pair (pk,sk)
-
More precisely:
-
∀
\forall
∀ (pk,sk) output by G
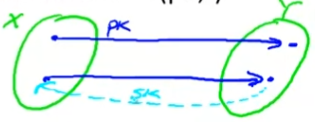
- ∀ x ∈ X \forall x \in X ∀x∈X: F − 1 ( s k , F ( p k , x ) ) = x F^{-1}(sk, F(pk,x)) = x F−1(sk,F(pk,x))=x
- 如下图所示
-
∀
\forall
∀ (pk,sk) output by G
Secure Trapdoor Functions (TDFs)
- (G,F,
F
−
1
F^{-1}
F−1) is secure if
F
(
p
k
,
⋅
)
F(pk, \cdot)
F(pk,⋅) is a “one-way” function:
- can be evaluated, but cannot be inverted without sk!
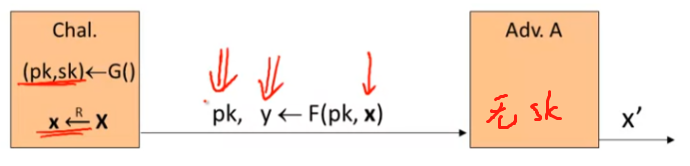
- Def: (G, F,
F
−
1
F^{-1}
F−1) is a secure TDF if for all efficient A:
- A d v O W [ A , F ] = P r [ x = x ′ ] Adv_{OW}[A,F] = Pr[x = x'] AdvOW[A,F]=Pr[x=x′] < negligible
- 无sk, 无法求逆
Public-key encryption from TDFs
-
构建Public-key encryption system 需要的工具:
- (G,F, F − 1 F^{-1} F−1): secure TDF X → Y X \rightarrow Y X→Y
- ( E s , D s ) (E_s, D_s) (Es,Ds): symmetric auth. encryption defined over ( K , M , C ) (K,M,C) (K,M,C)
- H: X → K X \rightarrow K X→K: a hash function
-
We construct a pub-key enc. system (G,E,D):
- Part1: Key generation G
- same as G for TDF
- 得到了key pair: (pk, sk)
- Part2: Encryption:
- E(pk,m):
- x ← R X x \leftarrow ^{R} X x←RX
- y ← F ( p k , x ) y \leftarrow F(pk,x) y←F(pk,x)
- k ← H ( x ) k \leftarrow H(x) k←H(x)
- x ← E s ( k , m ) x \leftarrow E_s(k,m) x←Es(k,m)
- output (y,c)
- E(pk,m):
- Part3: Decryption
- D(sk, ciphertext) = D(sk, (y,c))
- x ← F − 1 ( s k , y ) x \leftarrow F^{-1}(sk,y) x←F−1(sk,y)
- k ← H ( x ) k \leftarrow H(x) k←H(x)
- m ← D s ( k , c ) m \leftarrow D_s(k,c) m←Ds(k,c)
- output m
- Part1: Key generation G
-
In pictures:

- Security Theorem:
- If (G,F,
F
−
1
F^{-1}
F−1) is a secure TDF
- ( E s , D s ) (E_s, D_s) (Es,Ds) provides auth. enc.
- and
H
:
X
→
K
H: X \rightarrow K
H:X→K is a “random oracle”
- oracle 预告,甲骨文
- 意味着H是从X到K的随机映射
- 如SHA-256
- then (G,E,D) is
C
C
A
r
o
CCA^{ro}
CCAro secure
- ro: denote the fact that security is set in
random oracle model
- ro: denote the fact that security is set in
- If (G,F,
F
−
1
F^{-1}
F−1) is a secure TDF
- There is an ISO standard that defines this mode of encryption!
- 这种加密体制是一个标准 fine to use
Incorrect use of a Trapdoor Function (TDF)
- Never encrypt by applying F directly to plaintext!
- 直接使用F 进行加密是错误的!!!!
- 例如直接使用RSA进行加密是错误的!
- 即 E(pk,m): output
c
←
F
(
p
k
,
m
)
c\leftarrow F(pk,m)
c←F(pk,m)
- D(sk,c): output F − 1 ( s k , c ) F^{-1}(sk,c) F−1(sk,c)
- 直接使用F 进行加密是错误的!!!!
- Problems:
- Deterministic: cannot be semantically secure!
- 杨波老师现代密码学中说的是determinsitic public key encryption不可能是语义安全的!
- 从CPA game中即可得到
- Many attacks exist! (next segment!)
- Deterministic: cannot be semantically secure!
- Lesson:
- we should use public key encryption system like the ISO standard
- 而不是直接用TDF进行加密!!
现在:
- 了解了public key encryption system的构造
下面:
- 真正建立系统
- 以及介绍可能的attacks
6.2 Public Key Encryption from Trapdoor Permutations: RSA
6.2.1 The RSA Trapdoor Permutation
This segment:
- build a classic trapdoor function: RSA
Review: Trapdoor permutations
-
Def: a trapdoor func. X → Y X\rightarrow Y X→Y is a triple of efficient algs. (G, F, F − 1 F^{-1} F−1)
- G(): randomized alg. outputs a key pair (pk,sk)
- 产生密钥对
- F(pk, x): det. alg. that defines a function
X
→
X
X \rightarrow X
X→X
- Permutation: 所以是 X → X X \rightarrow X X→X
- F − 1 ( s k , y ) F^{-1}(sk,y) F−1(sk,y): inverts the function at y using sk
- G(): randomized alg. outputs a key pair (pk,sk)
-
Secure trapdoor permutation:
- The function F ( p k , ⋅ ) F(pk, \cdot) F(pk,⋅) is one-way without the trapdoor sk
Review: arithmetic mod composites
- Notation:
- Let N =
p
⋅
q
p \cdot q
p⋅q, where p, q are prime
- 意味着p, q ≈ \approx ≈ N \sqrt{N} N
- Z N = 0 , 1 , 2 , . . . , N − 1 \mathcal{Z}_{N} = {0,1,2, ..., N-1} ZN=0,1,2,...,N−1;
- Z N ∗ \mathcal{Z}^*_{N} ZN∗ = {invertible elements in Z N \mathcal{Z}_{N} ZN}
- Let N =
p
⋅
q
p \cdot q
p⋅q, where p, q are prime
- Facts:
- x ∈ x \in x∈ Z N \mathcal{Z}_{N} ZN is invertible ↔ \leftrightarrow ↔ gcd(x,N) = 1
- number of elements in
Z
N
∗
\mathcal{Z}^{*}_{N}
ZN∗ is
ϕ
(
N
)
\phi(N)
ϕ(N) = (p-1)(q-1) = N-p - q +1
- 当N很大时, ϕ ( N ) \phi(N) ϕ(N)与N非常接近
- 意味着从0~N随机选一个数,属于 Z N ∗ \mathcal{Z}^{*}_{N} ZN∗的概率非常大!
- Euler’s thm:
- ∀ x ∈ \forall x \in ∀x∈ ( Z N ∗ \mathcal{Z}^{*}_{N} ZN∗): x ϕ ( N ) = 1 x^{\phi(N)} = 1 xϕ(N)=1
The RSA trapdoor permutation
-
First published:
- Scientific American, Aug. 1977
- RSA: Rivest, Shamir, and Adleman
- From MIT
-
应用极广 very widely used:
- SSL/TLS: certificates and key-exchange
- Secure e-mail and file systems
- many others
-
由3部分组成: G, F, F − 1 F^{-1} F−1
- G():
- choose random primes
- p,q ≈ \approx ≈ 1024 bits
- Set N = pq
- Choose integers:
- e,d
- 满足ed = 1 mod ( ϕ ( N ) \phi(N) ϕ(N))
- output:
- pk = (N,e)
- e: encryption component
- sk = (N,d)
- d: decryption component
- pk = (N,e)
- choose random primes
- F(pk,x):
- Z N ∗ → Z N ∗ \mathcal{Z}^{*}_{N} \rightarrow \mathcal{Z}^{*}_{N} ZN∗→ZN∗
- RSA(x) = x e x^e xe (in Z N \mathcal{Z}_{N} ZN)
-
F
−
1
F^{-1}
F−1
- F − 1 ( s k , y ) = y d F^{-1}(sk,y) = y^d F−1(sk,y)=yd
-
y
d
y^d
yd = RSA(x)
d
^d
d =
x
e
d
x^{ed}
xed =
x
k
ϕ
(
N
)
+
1
x^{k\phi(N)} + 1
xkϕ(N)+1 = (
x
ϕ
(
N
)
x\phi(N)
xϕ(N))
k
^k
k
⋅
x
\cdot x
⋅x = x (in
Z
N
\mathcal{Z}_{N}
ZN)
- 原因:
- ed = 1 mod ( ϕ ( N ) \phi(N) ϕ(N));
- 欧拉theorem
- 原因:
The RSA assumption
-
RSA assumption:
- RSA is one-way permutation
-
For all efficient alg. A:
-
P
r
[
A
(
N
,
e
,
y
)
=
y
1
/
e
]
Pr[A(N,e,y) = y^{1/e}]
Pr[A(N,e,y)=y1/e] < negligible
- 即d (private key)未知时无法decryption
- where p,q
←
R
\leftarrow ^ R
←R n-bit primes
- N ← \leftarrow ← pq
- $y \leftarrow ^R $ Z N ∗ \mathcal{Z}^{*}_{N} ZN∗
-
P
r
[
A
(
N
,
e
,
y
)
=
y
1
/
e
]
Pr[A(N,e,y) = y^{1/e}]
Pr[A(N,e,y)=y1/e] < negligible
Review: RSA pub-key encryption
-
构建Public-key encryption system 需要的工具:
- (G,F, F − 1 F^{-1} F−1): secure TDF X → Y X \rightarrow Y X→Y
- ( E s , D s ) (E_s, D_s) (Es,Ds): symmetric auth. encryption defined over ( K , M , C ) (K,M,C) (K,M,C)
- H: X → K X \rightarrow K X→K: a hash function
-
We construct a pub-key enc. system (G,E,D):
- Part1: Key generation G
- generate RSA params
- pk = (N,e), sk = (N,d)
- Part2: Encryption:
- (1) choose random x in Z N Z_N ZN
- (2) y ← R S A ( x ) = x e y \leftarrow RSA(x) = x^e y←RSA(x)=xe, k ← H ( x ) k \leftarrow H(x) k←H(x)
- (3) output (y, E s ( k , m ) E_s(k,m) Es(k,m))
- Part3: Decryption
- D(sk, (y,c)):
- output D s ( H ( R S A − 1 ( y 0 ) ) , c ) D_s(H(RSA^{-1}(y0)), c) Ds(H(RSA−1(y0)),c)
- D(sk, (y,c)):
- Part1: Key generation G
Textbook RSA is insecure
警告: RSA不能直接用来作为加密框架!
- Textbook RSA encryption:
- public key: (N,e); secret key (N,d)
- Encryption: c ← m e \leftarrow m^e ←me (in Z N \mathcal{Z}_{N} ZN)
- Decryption: c d → m c^d \rightarrow m cd→m
- Insecure cryptosystem!!!
- is not semantically secure and many attacks exist!
-
⇒
\Rightarrow
⇒ The RSA trapdoor permutation is not an encryption scheme!
- 仅仅是一个trapdoor permutation
- 很多教科书没有区分RSA加密框架和RSA陷门置换!!
- 实际上绝对不能用RSA陷门置换直接加密!!(如下例 ↓ \downarrow ↓)
A simple attack on textbook RSA
-
Web browser 和 Web Server通过RSA对一个session key进行加密交换
-
直接使用RSA加密会不安全!
- suppose k is 64 bits:
k
∈
k \in
k∈ {0,1,2, …,
2
64
2^{64}
264}
- 转换为一个integer
- Eve sees: c = k e c = k^e c=ke is Z N \mathcal{Z}_{N} ZN
- 攻击方法:
- If
k
=
k
1
⋅
k
2
k = k_1 \cdot k_2
k=k1⋅k2 where
k
1
,
k
2
<
2
34
k_1 ,k_2 < 2^{34}
k1,k2<234 (概率约为20%)
- then c / k 1 e = k 2 e c/k_1^{e} = k^{e}_2 c/k1e=k2e in Z N \mathcal{Z}_{N} ZN
- Meet in the middle attack 中间相遇攻击
- Step 1: build table:
c
/
1
e
c/1^e
c/1e,
c
/
2
e
c/2^e
c/2e,
c
/
3
e
c/3^e
c/3e, … ,
c
/
(
2
34
)
e
c/(2^{34})^e
c/(234)e.
- time: 2 34 2^{34} 234
- step 2: for
k
2
=
0
,
.
.
.
,
2
34
k_2 = 0, ..., 2^{34}
k2=0,...,234, test if
k
2
e
k^{e}_2
k2e is in table:
- time: 2 34 2^{34} 234
- Step 1: build table:
c
/
1
e
c/1^e
c/1e,
c
/
2
e
c/2^e
c/2e,
c
/
3
e
c/3^e
c/3e, … ,
c
/
(
2
34
)
e
c/(2^{34})^e
c/(234)e.
- Output matching ( k 1 , k 2 ) (k_1, k_2) (k1,k2)
- If
k
=
k
1
⋅
k
2
k = k_1 \cdot k_2
k=k1⋅k2 where
k
1
,
k
2
<
2
34
k_1 ,k_2 < 2^{34}
k1,k2<234 (概率约为20%)
- Total attack time:
- ≈ 2 40 < < 2 64 \approx 2^{40} << 2^{64} ≈240<<264
- suppose k is 64 bits:
k
∈
k \in
k∈ {0,1,2, …,
2
64
2^{64}
264}
-
Never never use RSA directly to encrypt!!!
- 要使用标准的框架,如ISO定义的框架
6.2.2 PKCS 1
How RSA is used in practice
RSA encryption in practice
-
Never use textbook RSA
-
RSA in practice:
- (since ISO standard is not often used)
- 在使用RSA之前必须进行preprocessing!
- 例如:
- 输入的msg (要交换的key): AES key (128 bits)
- 将其扩展为 2048 bits
- 之后再使用RSA进行encryption
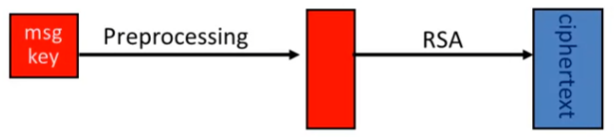
-
Main questions:
- How should the preprocessing be done?
- Can we argue about security of resulting system
PKCS 1 V1.5
- PKCS 1 mode 2:
- mode 2: encryption
- mode 1: signatures
- FF: 16 bits of 1
- 02: 表示mode
- 加密:
- the string (2048 bits) 输入到RSA function中
- raised to the power of e mod N
- 最终得到ciphertext
- the string (2048 bits) 输入到RSA function中
- 解密:
- 1 RSA解密
- 2 根据02, 确定是encryption mode
- 3 删除FF及之前的部分,得到的即为msg
- mode 2: encryption
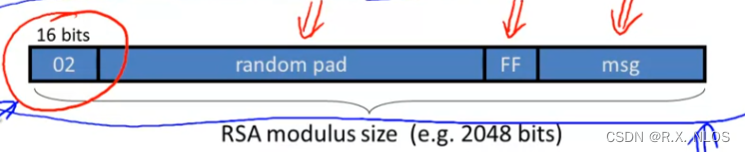
- Resulting value is RSA encrypted
- Widely deployed. e.g., in HTTPS
该方法并没有security proof
- 事实证明,没有security proof的算法常常会存在elegant attack!
Attack on PKCS 1 v1.5 (Bleichenbacher 1998)
- PKCS 1 used in HTTPS:

-
⇒ \Rightarrow ⇒ attacker can test if 16 MSBs of plaintext = ‘02’
- 尽管只泄露了2 bit, 但已经可以让attacker恢复全部明文!
-
Chosen-ciphertext attack:
- to decrypt a given ciphertext c, do:
- 1 Choose r ∈ r \in r∈ Z N \mathcal{Z}_{N} ZN
- 2 Compute
c
′
←
r
e
⋅
c
=
(
r
⋅
P
K
C
S
1
(
m
)
)
e
c' \leftarrow r^e \cdot c = (r\cdot PKCS1(m))^e
c′←re⋅c=(r⋅PKCS1(m))e
- just multiply plaintext by r
- the r is determined by the attacker
- 重复该步骤很多次,能够重建全部的PKCS1(m)!
- 即全部的明文
- 具体原因见next slide
- 3 send c’ to web server and use response
- to decrypt a given ciphertext c, do:
Baby Bleichenbacher
- 方便理解上一页 (Bleichenbacher) 的一个简单函数
- Compute x ← c d x\leftarrow c^d x←cd in Z N \mathcal{Z}_{N} ZN

-
Suppose N is N = 2 n N = 2^n N=2n (an invalid RSA modulus), Then:
- Sending c reveals msb(x)
- 即能够确定 m s b 1 ( x ) msb_1(x) msb1(x)
- Sending
2
e
⋅
c
=
(
2
x
)
e
2^e \cdot c = (2x) ^e
2e⋅c=(2x)e in
Z
N
\mathcal{Z}_{N}
ZN
- reveals msb(2x mod N) = m s b 2 ( x ) msb_2(x) msb2(x)
- Sending
4
e
⋅
c
4^e \cdot c
4e⋅c
- reveals msb(4x mod N) = m s b 3 ( x ) msb_3(x) msb3(x)
- 以此类推
- 即可获得entire plaintext
- Sending c reveals msb(x)
-
How to define this attack? 见下文
HTTPS Defense (RFC 5246)
-
思路
- 1 Generate a string R of 46 random bytes
- 解密后,发现Plaintext不对,这时不报错,而是直接认为plaintext就是R!
- then, the protocol will fail later on
- 2 Decrypt the message to recover the plaintext
- 3 If the PKCS #1 padding is not correct
- p r e m a s t e r s e c r e t = R pre_master_secret = R premastersecret=R
- 1 Generate a string R of 46 random bytes
-
Most web servers today implement this version!
但这上述bug也引发了一个思考:
- PKCS 是否应该全盘改动?
PKCS v 2.0: OAEP
- New preprocessing function: OAEP
- check pad on encryption
- reject CT if invalid
- 补全长度:与RSA算法一致,如2047 bits
- 最后将整个concate的text 进行RSA加密
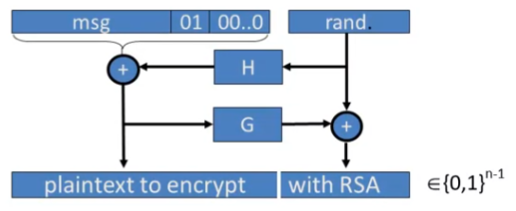
-
OAEP: Optimal Asymmetric Encryption Padding
- optimal: 是指the ciphertext的长度是最短的!
- ciphertext的长度就是RSA输出的长度
- no trailing values that are appended to the ciphertext
- 但ISO就需要额外的padding
-
Thm [FOPS’01]:
- RSA is a trap-door permutation
-
⇒
\Rightarrow
⇒ RSA-OAEP is CCA secure when H,G are random oracles
- 需要依赖于RSA! 如果是一个普通的trap-door permutation, 怎么办?
- 见下一页
- 需要依赖于RSA! 如果是一个普通的trap-door permutation, 怎么办?
-
in practice: use SHA-256 for H and G
OAEP Improvements
- OAEP+: [Shoup’ 01]
-
∀
\forall
∀ trap-door permutation F
- F-OAEP is CCA secure when H,G,W are random oracles
- During decryption, validate W(m,r) field
-
∀
\forall
∀ trap-door permutation F

- SAEP+: [B’ 01]
- RSA (e=3) is a trap-door perm
- ⇒ \Rightarrow ⇒ RSA-SAEP+ is CCA secure when H,W are rnadom oracle
- 解密:
- ( x , r ) ⟵ R S A − 1 ( s k , c t ) , ( m , w ) ⟵ x ⊕ H ( r ) , (x, r) \longleftarrow RSA^{-1}(s k, c t), \quad(m, w) \longleftarrow x \oplus H(r), \quad (x,r)⟵RSA−1(sk,ct),(m,w)⟵x⊕H(r), output m m m if w = W ( m , r ) w=W(m, r) w=W(m,r)
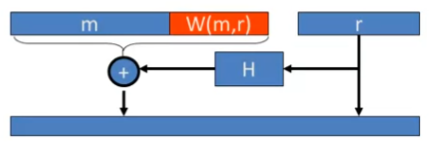
Subtleties in implementing OAEP
- 解码技巧:
OAEP-decrypt(ct):
error = 0
...
if (RSA^{-1} (ct) > 2^{n-1}) # 取值范围约束
{error = 1; goto exit;}
...
if (pad(OAEP^{-1}(RSA^{-1}(ct))) != "01000") # padding 约束
{error = 1; goto exit;}
-
但应注意采取措施防止计时攻击
- Problem: timing information leaks type of error
- ⇒ \Rightarrow ⇒ Attacker can decrypt any ciphertext
- Problem: timing information leaks type of error
-
Lesson: Do not implement RSA-OAEP yourself!
Next segment:
- The security of RSA trapdoor permutation
6.3 Public Key Encryption from Trapdoor Permutations: Attacks
6.3.1 Is RSA a One-Way Function?
注意:RSA 不是对数运算!!!!所以不基于离散对数!!
- 离散对数: 已知 g x ( m o d N ) g^x (mod \quad {N}) gx(modN) 和 g, 求x
- RSA, 已知 x e ( m o d N ) x^e (mod \quad {N}) xe(modN) 和 e, 求x
- RSA更像是开方运算
This segment:
- Is RSA a one-way permutation?
- 不知道secret key时,是否无法求逆
Is RSA a one-way permutation?
- To invert the RSA one-way function (without d), attacker must compute:
- x from c = x e ( m o d N ) c = x^e (mod \quad {N}) c=xe(modN)
- How hard is computing e’th roots modulo N?
- Best known algorithm:
- Step 1: factor N (hard)
- Step 2: compute e’th roots modulo p and q
Shortcuts?
- Must one factor N in order to compute e’th roots?
- To prove no shortcut exists show a reduction:
- Efficient algorithm for e’th roots mod N
- ⇒ \Rightarrow ⇒ efficient algorithm for factoring N
- 改为证明(已reduction):能够求解RSA的算法必然能够进行大数分解
- 意味着 不存在比大数分解更快的RSA算法
- Oldest problem in public key cryptography
- 该问题尚无定论!
-
e
=
3
⇒
e = 3 \Rightarrow
e=3⇒ Factor N??
- 尚无定论
-
e
=
2
⇒
e = 2 \Rightarrow
e=2⇒ Factor N
- YEs ! 但是RSA中的e 不可能是偶数
- e ⋅ d e \cdot d e⋅d = 1 ( m o d N ) (mod \quad {N}) (modN)
- ⇒ \Rightarrow ⇒ g c d ( e , ϕ ( N ) ) = 1 gcd(e, \phi(N)) = 1 gcd(e,ϕ(N))=1
- ϕ ( N ) = ( p − 1 ) ( q − 1 ) \phi(N) = (p-1)(q-1) ϕ(N)=(p−1)(q−1)为偶数
- 因此e不是偶数!
- YEs ! 但是RSA中的e 不可能是偶数
-
e
=
3
⇒
e = 3 \Rightarrow
e=3⇒ Factor N??
- Efficient algorithm for e’th roots mod N
- 目前公认:
- 要破解RSA,就要对大数进行分解!
- 这一点是目前公认的、SOTA的方法!
- 尽管无法证明
How Not to improve RSA’s performance
- “Not”:
- 意思是很多方法试图提高RSA的性能
- 但是他们都错了,反而成了Not 的方法
- To speed up RSA decryption use small private key d
- d ≈ 2 128 d\approx 2^{128} d≈2128
- c d = m ( m o d N ) c^d = m (mod \quad {N}) cd=m(modN)
- 但事实上:
- Wiener’87: if
d
<
N
0.25
d < N^{0.25}
d<N0.25, then RSA is insecure
- 例如N = 2 2 048 2^2048 22048
- d就不能小于 2 5 12 2^512 2512
- 理由in the next slide
- BD’98: if d < N 0.292 d < N^{0.292} d<N0.292, then RSA is insecure
- Wiener’87: if
d
<
N
0.25
d < N^{0.25}
d<N0.25, then RSA is insecure
- Insecure: private key d can be found from (N,e)
Wiener’s attack
- Recall:
-
e
⋅
d
=
1
(
m
o
d
ϕ
(
N
)
)
e\cdot d = 1(mod \quad {\phi(N)})
e⋅d=1(modϕ(N))
- ⇒ \Rightarrow ⇒ ∃ k ∈ Z \exist k \in Z ∃k∈Z: e ⋅ d = k ⋅ ϕ ( N ) + 1 e\cdot d = k \cdot \phi(N) + 1 e⋅d=k⋅ϕ(N)+1
- ⇒ \Rightarrow ⇒ ∣ N − φ ( N ) ∣ ≤ p + q ≤ 3 N |N-\varphi(N)| \leq p+q \leq 3 \sqrt{N} ∣N−φ(N)∣≤p+q≤3N
-
⇒
\Rightarrow
⇒ if
d
≤
N
0.25
/
3
d\leq N^{0.25}/3
d≤N0.25/3, then:
- |e/N - k/d| ≤ \leq ≤ 1 2 d 2 \frac{1}{2d^2} 2d21
- 证明见视频
- e/N: 已知
- 而k/d又与e/N非常非常接近
-
e
⋅
d
=
1
(
m
o
d
ϕ
(
N
)
)
e\cdot d = 1(mod \quad {\phi(N)})
e⋅d=1(modϕ(N))
- Continued function expansion of e/N gives k/d
- 能够推导出log(N)种可能的k/d值
- 再进行遍历尝试
- 即可破解k/d
- 然后:
- c ⋅ d = 1 ( m o d k ) ⇒ gcd ( d , k ) = 1 ⇒ c \cdot d=1(\bmod k) \Rightarrow \operatorname{gcd}(d, k)=1 \Rightarrow c⋅d=1(modk)⇒gcd(d,k)=1⇒ can find d d d from k / d k / d k/d
- 即可得到d
6.3.2 RSA in Practice
This segment:
- How RSA is used in practice
- to conclude this module
RSA with Low public exponent
- To speed up RSA encryption use a small e:
- c = m e ( m o d N ) c = m^e (mod \quad {N}) c=me(modN)
- Minimum value: e = 3
- gcd(e, ϕ ( N ) \phi(N) ϕ(N)) = 1
- Recommended value:
- e = 65537 = 2 16 + 1 e = 65537 = 2^{16} + 1 e=65537=216+1
- Encryption: 17 multiplications
- Asymmetry of RSA:
- Fast enc. / slow dec.
- decryption:
X
65537
(
m
o
d
N
)
X^{65537} (mod \quad {N})
X65537(modN)
- need the order of 2000 multiplications
- a speed-up method: RSA-CRT, but still much slower than the encryption
- decryption:
X
65537
(
m
o
d
N
)
X^{65537} (mod \quad {N})
X65537(modN)
- EIGammal (next module) approx. same time for both
- Fast enc. / slow dec.
Key Lengths
- Security of public key system should be comparable to security of symmetric cipher:

Implementation attacks
-
Timing attack: (Kecher 97)
- The time it takes to compute c d ( m o d N ) c^d (mod \quad {N}) cd(modN) can expose d
-
Power attack: (Kocher 99)
- The power consumption of a smartcard while it is computing c d ( m o d N ) c^d (mod \quad {N}) cd(modN) can expose d
-
Faults attack: (BDL 97)
- A computer error during c d ( m o d N ) c^d (mod \quad {N}) cd(modN) can expose d
- just one error completely reveals the secret key
- A common defense: check output (e = c mod N ??)
- take less time: 10% slowdown
-
Lesson:
- 按照RSA定义去实现仍无法避免诸多攻击!
- 应尽量避免使用未经验证的实现方法
An example Fault Attack on RSA (CRT)
- A common implementation of RSA decryption:
-
x
=
c
d
x = c^d
x=cd in
Z
N
\mathcal{Z}_{N}
ZN
- 通常的解密方法:先浸塑p上的,再计算q上的,合到一起就能得到最后结果
- decrypt mod p: x p = c d x_p = c^d xp=cd in Z p \mathcal{Z}_{p} Zp
- decrypt mod q: x q = c d x_q = c^d xq=cd in Z q \mathcal{Z}_{q} Zq
- combine them to get x = c d x = c^d x=cd Z N \mathcal{Z}_{N} ZN
- 这样可以把解密加速四倍, 但会受到Fault Attack!
-
x
=
c
d
x = c^d
x=cd in
Z
N
\mathcal{Z}_{N}
ZN
- Suppose error occurs when computing
x
q
x^q
xq, but no error in
x
p
x_p
xp
- 处理器运算时出现了错误
- Then:
- output is x’ where x ′ = c d x' = c^d x′=cd in Z p \mathcal{Z}_{p} Zp
- but x ′ ≠ c d x' \not ={c^d} x′=cd in Z q \mathcal{Z}_{q} Zq
-
⇒
\Rightarrow
⇒:
- ( x ′ ) e (x')^e (x′)e in Z p \mathcal{Z}_{p} Zp
- but ((x’)^e) ≠ c \not ={c} =c in Z q \mathcal{Z}_{q} Zq
-
⇒
\Rightarrow
⇒:
- gcd(
(
x
′
)
e
−
c
,
N
(x')^e -c, N
(x′)e−c,N) = p
- 因为p能够整除 ( x ′ ) e − c (x')^e -c (x′)e−c,但是q不能整除 ( x ′ ) e − c (x')^e -c (x′)e−c
- 得到q,意味着完成了因式分解!!!
- gcd(
(
x
′
)
e
−
c
,
N
(x')^e -c, N
(x′)e−c,N) = p
- 从而完成密钥的恢复
- 解决方法:验证输出的正确性
RSA Key Generation Trouble [Heninger et al. / Lenstra et al.]
-
如果RSA产生密钥时熵很小,就会产生问题
-
OpenSSL RSA key generation (abstract):
# 若随机数生成器的熵很小,就会出问题!
prng.seed(seed)
p = prng.generate_random_prime()
prng.add_randomness(bits)
q = prng.generate_random_prime()
N = p*q
- Suppose poor entropy at startup:
- same p will be generated by multiple devices
- but different q
- N 1 , N 2 N_1, N_2 N1,N2: RSA keys from different devices ⇒ \Rightarrow ⇒ gcd( N 1 N_1 N1, N 2 N_2 N2) = p
- 相当于完成了因式分解
- 因此不安全
- same p will be generated by multiple devices
Experiment: factors 0.4% of public HTTP keys!!!
Lesson:
- Make sure random number generator is properly seeded when generating keys
- 事实上,不管是RSA, EIGammal, 还是对称密码,这一点都需要满足!
Further reading
- 1998, Why chosen ciphertext security matters
- 密码必须是chosen ciphertext security的
- 1999, Twenty years of attacks on the RSA cryptosystem
- 一个survey
- 2001, OAEP reconsidered
- 2004, Key lengths
- 如何为密码系统选择密钥长度
6.4 Public Key Encryption From Diffie-Hellman: EIGamal
6.4.1 The EIGamal Public-key system
This segment
- 另一种加密框架 EIGamal
- are built from Diffie-Hellman protocol
Recap: public key encryption (Gen, E, D) & Applications
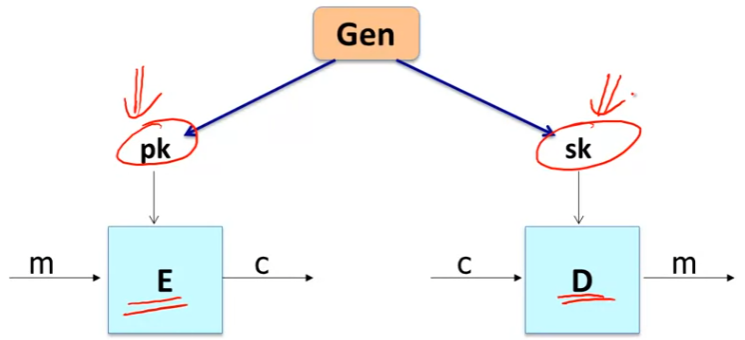
Applications:
- Key exchange:
- e.g., in HTTPS
- Encryption in non-interactive settings:
- Secure Email:
- Bob has Alice’s Pub-Key and Sends her an email
- Encrypted File Systems
- 例如下图是Bob 加密文件,但A也可以访问的情况
- A只需要用自己的secret key解密即可
- A和B之间不需要交互
- Key escrow: data recovery without Bob’s key
- 密钥第三方(如公司)托管
- 把Alice换成escrow即可
- Secure Email:
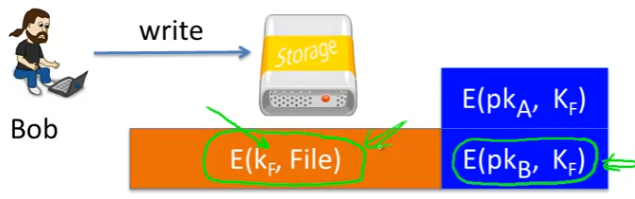
Constructions
- This week: two families of public-key encryption schemes
- Previous lecture:
- based on trapdoor functions
- such as RSA
- Schemes: ISO standard, OAEP+
- based on trapdoor functions
- This lecture:
- based on Diffie-Hellman protocol
- Schemes: EIGamal encryption and variants (e.g., used in GPG)
- GPG: an email encryption system (GNU privacy guard)
- Security goals:
- chosen ciphertext security
Review: the Diffie-Hellman protocol
-
Fix a finite cyclic group G of order n
- e.g., G = Z p ∗ \mathcal{Z}^{*}_{p} Zp∗
- 或者是the points of an 椭圆曲线
- order n: means g n = 1 g^n = 1 gn=1
-
Fix a generator g in G:
- 即 G = { 1 , g , g 2 , g 3 , … , g n − 1 } \mathrm{G}=\left\{1, g, \mathrm{~g}^{2}, \mathrm{~g}^{3}, \ldots, \mathrm{g}^{\mathrm{n}-1}\right\} G={1,g, g2, g3,…,gn−1}
-
Step:
- Alice: choose random a in {1,2, …, n}
- Bob: choose random b in {1,2, …, n}
- generated session key: g a b g^{ab} gab
- 注意:
- A = g a A = g^a A=ga 和 B = g b B = g^b B=gb 均是 G中的元素!
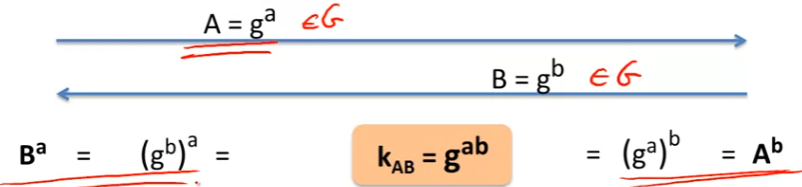
EIGamal: converting to pub-key enc.
-
Fix a finite cyclic group of order n
- e.g., G = Z p ∗ \mathcal{Z}^{*}_{p} Zp∗
-
Fix a generator g in G:
- 即 G = { 1 , g , g 2 , g 3 , … , g n − 1 } \mathrm{G}=\left\{1, g, \mathrm{~g}^{2}, \mathrm{~g}^{3}, \ldots, \mathrm{g}^{\mathrm{n}-1}\right\} G={1,g, g2, g3,…,gn−1}
-
Step:
- 1 Key generation:
- Alice: choose random a in {1,2, …, n} and compute A = g a A = g^a A=ga
- public key: A
- private key: a
- 从A得到a的过程是一个离散对数问题!
- 2 Bob 希望加密消息m,并发送给A (E)
- Bob: choose random b in {1,2, …, n}
- Bob compute g a b = A b g^{ab} = A^b gab=Ab
- Bob derive symmetric key k
- 根据 g a b g^{ab} gab
- ct = [ B = g b B = g^b B=gb, encrypt message m with k]
- 3 Alice 解密消息:
- Alice compute g a b = B a g^{ab} = B^a gab=Ba
- Alice derive k
- 根据 g a b g^{ab} gab
- 即可用k完成对m的解密
- 1 Key generation:
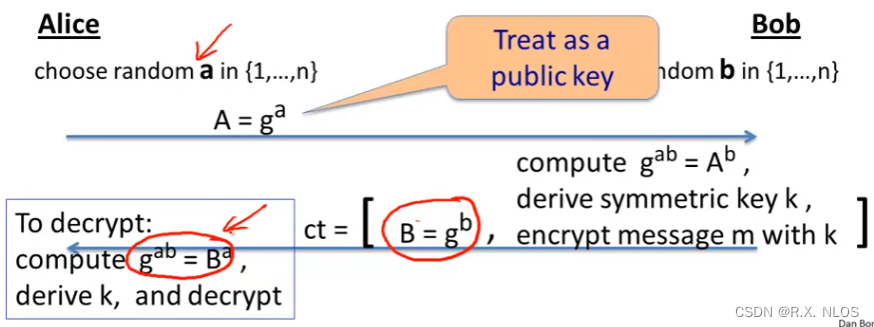
- 注意: EI Gammal每次的加密结果并不同
- 因为Bob每次加密时都会随机选取一个b
- 与RSA不一样
更加细节的描述: ↓ \downarrow ↓
The EIGamal system (a modern view)
- G: finite cyclic group of order n
- ( E s , D s ) (E_s, D_s) (Es,Ds): symmetric auth. encryption defined over (K,M,C)
- H: G 2 → K G^2 \rightarrow K G2→K: a hash function
The pub-key enc. system (Gen, E, D):
- 1 Key generation Gen:
- choose random generator g in G and random a in Z n Z_n Zn
- output sk = a; pk = (g, h = g a g^a ga)
- 2 Encryption E(pk=(g,h), m):
-
b
←
Z
n
,
u
⟵
g
b
,
v
⟵
h
b
b \leftarrow Z_{n}, u \longleftarrow g^{b}, v \longleftarrow h^{b}
b←Zn,u⟵gb,v⟵hb
- u相当于 B = g b B = g^b B=gb, v相当于 g a b g^{ab} gab
- k ⟵ H ( u , v ) , c ⟵ E s ( k , m ) \mathrm{k} \longleftarrow \mathrm{H}(\mathrm{u}, \mathrm{v}), \mathrm{c} \longleftarrow \mathrm{E}_{\mathrm{s}}(\mathrm{k}, \mathrm{m}) k⟵H(u,v),c⟵Es(k,m)
- output (u,c)
-
b
←
Z
n
,
u
⟵
g
b
,
v
⟵
h
b
b \leftarrow Z_{n}, u \longleftarrow g^{b}, v \longleftarrow h^{b}
b←Zn,u⟵gb,v⟵hb
- 3 Decryption D(sk = a, (u,c)):
- v ← u a v \leftarrow u^a v←ua
- k ← H ( u , v ) k\leftarrow H(u,v) k←H(u,v)
- m ← D s ( k , c ) m \leftarrow D_s(k,c) m←Ds(k,c)
- output m

EIGamal performance

- Encryption: 2 exp (fixed basis) (计算u, 计算v)
- Can pre-compute [ g ( 2 ∧ i ) , h ( 2 ∧ i ) \left[g^{\left(2^{\wedge} i\right)}, h^{\left(2^{\wedge} i\right)}\right. [g(2∧i),h(2∧i) for i = 1 , … , log 2 n ] \left.i=1, \ldots, \log _{2} n\right] i=1,…,log2n]
- 3X speed-up (or more)
- 如果g和h不固定,那就没办法加速
- 如果encryption是瓶颈,那就选择RSA
- Decryption: 1 exp. (variable basis)
Next segment:
- Why is EIGamal system chosen ciphertext secure?
- under what assumpetions?
6.4.2 EIGamal Security
Computational Diffie-Hellman Assumption
- G: finite cuclic group of order n
假设1: 最弱的假设 CDH 假设
- computational DH假设
- Comp. DH (CDH) assumpation holds in G if:
- g , g a , g b ⇏ g a b g, g^{a}, g^{b} \not \Rightarrow g^{a b} g,ga,gb⇒gab
- 更专业的描述 (more precisely):
- for all efficient algs. A:
- Pr [ A ( g , g a , g b ) = g a b ] < [A(g,g^a,g^b) = g^{ab}]< [A(g,ga,gb)=gab]< negligible
- where $g\leftarrow $ {generators of G}, a,b ← \leftarrow ← Z N \mathcal{Z}_{N} ZN
- for all efficient algs. A:
但CDH假设尚不足以证明EIGamal的semantic security, 下面引入更强的假设 HDH
Hash Diffie-Hellman Assumption
-
G: finite cyclic group of order n
-
H: G 2 → K G^2 \rightarrow K G2→K
- a hash function
-
Def: Hash-DH (HDH) assumption holds for (G,H) if:
-
(
g
,
g
a
,
g
b
,
H
(
g
b
,
g
a
b
)
)
≈
p
(
g
,
g
a
,
g
b
,
R
)
\left(g, g^{a}, g^{b}, H\left(g^{b}, g^{a b}\right)\right) \approx_{p}\left(g, g^{a}, g^{b}, R\right)
(g,ga,gb,H(gb,gab))≈p(g,ga,gb,R)
- where g ← g\leftarrow g← {generators of G}, a , b ← a,b \leftarrow a,b← Z N \mathcal{Z}_{N} ZN, R ← K R\leftarrow K R←K
- 也就是说新增了H必须是理想Hash的条件
-
(
g
,
g
a
,
g
b
,
H
(
g
b
,
g
a
b
)
)
≈
p
(
g
,
g
a
,
g
b
,
R
)
\left(g, g^{a}, g^{b}, H\left(g^{b}, g^{a b}\right)\right) \approx_{p}\left(g, g^{a}, g^{b}, R\right)
(g,ga,gb,H(gb,gab))≈p(g,ga,gb,R)
-
注意: HDH假设比CDH假设更强!
- 有些系统满足CDH假设,但是不满足HDH假设!
Example: 一个是符合CDH但不符合HDH的system
- Suppose K =
{
0
,
1
}
128
\{0,1 \}^{128}
{0,1}128 and
- H:
G
2
←
K
G^2 \leftarrow K
G2←K only outputs strings in K that begins with 0
- 即 for all x,y: msb(H(x,y)) = 0
- H:
G
2
←
K
G^2 \leftarrow K
G2←K only outputs strings in K that begins with 0
- Can Hash-DH hold for (G,H)?
ANs: No, Hash-DH is easy to break in this case!!
- 满足CDH假设,但是不满足HDH假设!
EIGamal is sem. secure under Hash-DH
首先回顾EIGamal加密系统
The pub-key enc. system (Gen, E, D):
- 1 Key generation Gen:
- choose random generator g in G and random a in Z n Z_n Zn
- output sk = a; pk = (g, h = g a g^a ga)
- 2 Encryption E(pk=(g,h), m):
-
b
←
Z
n
,
u
⟵
g
b
,
v
⟵
h
b
b \leftarrow Z_{n}, u \longleftarrow g^{b}, v \longleftarrow h^{b}
b←Zn,u⟵gb,v⟵hb
- u相当于 B = g b B = g^b B=gb, v相当于 g a b g^{ab} gab
- k ⟵ H ( u , v ) , c ⟵ E s ( k , m ) \mathrm{k} \longleftarrow \mathrm{H}(\mathrm{u}, \mathrm{v}), \mathrm{c} \longleftarrow \mathrm{E}_{\mathrm{s}}(\mathrm{k}, \mathrm{m}) k⟵H(u,v),c⟵Es(k,m)
- output (u,c)
-
b
←
Z
n
,
u
⟵
g
b
,
v
⟵
h
b
b \leftarrow Z_{n}, u \longleftarrow g^{b}, v \longleftarrow h^{b}
b←Zn,u⟵gb,v⟵hb
- 3 Decryption D(sk = a, (u,c)):
- v ← u a v \leftarrow u^a v←ua
- k ← H ( u , v ) k\leftarrow H(u,v) k←H(u,v)
- m ← D s ( k , c ) m \leftarrow D_s(k,c) m←Ds(k,c)
- output m
下面证明语义安全:
- 上下两个等号:
- 基于Hash函数的理想性
- 左边的等号:
- 基于对称加密的语义安全
- 密文不体现关于密文的任何信息
- 基于对称加密的语义安全
- 因此即可证明HDH下的语义安全

但这样仍无法证明CCA security!
- 需要更强的假设 – IDH
EIGamal chosen ciphertext security?
- To prove chosen ciphertext security need stronger assumption
- Interactive Diffie-Hellman (IDH) in group G:
- 再ODH的基础上赋予了Adv. 更强的一个能力:
- Adv. 可以询问挑战者 (u,v)是否满足 ( u ) a = v (u)^a = v (u)a=v.
- 添加该能力的原因仅仅是为了满足CCA security
- 再ODH的基础上赋予了Adv. 更强的一个能力:
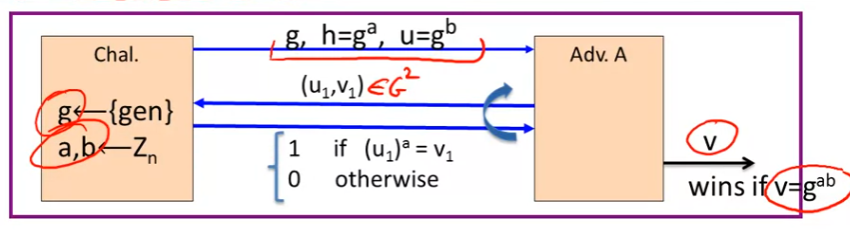
- IDH holds in G if Pr [ \operatorname{Pr}[ Pr[ A outputs g a b g^{ab} gab] < < < negligible
EIGamal chosen ciphertext security
-
Security theorem:
- If
- IDH holds in the group G:
- ( E s , D s ) (E_s, D_s) (Es,Ds) provides auth. enc.
- H: G 2 ← G^2\leftarrow G2← K is a “random oracle”
- Then
- EIGamal is
C
C
A
r
o
CCA^{ro}
CCAro secure
- ro: means random oracle model
- EIGamal is
C
C
A
r
o
CCA^{ro}
CCAro secure
- If
-
Questions: 待解决的问题
- 1 Can we prove CCA security based on HDH
- 即避免IDH中奇怪的询问能力
- 2 Can we prove CCA security based on CDH (without random oracle)
- 即使用具体的Hash函数即可证明
- 1 Can we prove CCA security based on HDH
6.4.3 EIGamal Variants With Better Security
Last segment:
- 在有些奇怪的假设下说明了EIGamal CCA Security
This segment:
- Look at variants of EIGamal that have a much better CCA security analysis
Review: EIGamal Encryption
The pub-key enc. system (Gen, E, D):
- 1 Key generation Gen:
- choose random generator g in G and random a in Z n Z_n Zn
- output sk = a; pk = (g, h = g a g^a ga)
- 2 Encryption E(pk=(g,h), m):
- b ← Z n , u ⟵ g b , v ⟵ h b b \leftarrow Z_{n}, u \longleftarrow g^{b}, v \longleftarrow h^{b} b←Zn,u⟵gb,v⟵hb
- k ⟵ H ( u , v ) , c ⟵ E s ( k , m ) \mathrm{k} \longleftarrow \mathrm{H}(\mathrm{u}, \mathrm{v}), \mathrm{c} \longleftarrow \mathrm{E}_{\mathrm{s}}(\mathrm{k}, \mathrm{m}) k⟵H(u,v),c⟵Es(k,m)
- output (u,c)
- 3 Decryption D(sk = a, (u,c)):
- v ← u a v \leftarrow u^a v←ua
- k ← H ( u , u a ) k\leftarrow H(u,u^a) k←H(u,ua)
- m ← D s ( k , c ) m \leftarrow D_s(k,c) m←Ds(k,c)
- output m
EIGamal Chosen Ciphertext Security
-
Security Theorem:
- If IDH holds in the group G:
- ( E s , D s ) (E_s, D_s) (Es,Ds) provides auth. enc.
- and H : G 2 → K H: G^2 \rightarrow K H:G2→K is a “random oracle”
- Then
- EIGamal is C C A r o CCA^{ro} CCAro secure
- If IDH holds in the group G:
-
Question: Can we prove CCA security based on CDH g , g a , g b ⇏ g a b g, g^{a}, g^{b} \nRightarrow g^{a b} g,ga,gb⇏gab
-
Answer: 有两种方法实现:
- 方法1 Use Group G where CDH = IDH (a.k.a, bilibear group)
- 方法2 Change the EIGamal system
-
下面介绍方法2中的一个
Variants: twin EIGamal [CKS’ 08]
-
KeyGen: g ← g \leftarrow g← {generators of G}
- a 1 , a 2 ← Z n a1, a2 \leftarrow Z_n a1,a2←Zn
- Output
- pk = ( g , h 1 = g a 1 , h 2 = g a 2 g, h_{1}=g^{a 1}, h_{2}=g^{a 2} g,h1=ga1,h2=ga2)
- sk = (a1,a2)
-
Encryption: E(pk=(g, h1, h2), m):
- $b \leftarrow $ Z N \mathcal{Z}_{N} ZN
- k ← H ( g b , h 1 b , h 2 b ) k \leftarrow H(g^b, h_1 ^b, h_2 ^b) k←H(gb,h1b,h2b)
- c ← E S ( k , m ) c \leftarrow E_S(k,m) c←ES(k,m)
- output ( g b , c ) (g^b, c) (gb,c)
-
Decryption: D(sk = (a1,a2), (u,c))
- k ⟵ H ( u , u a 1 , u a 2 ) \mathrm{k} \longleftarrow \mathrm{H}\left(\mathrm{u}, \mathrm{u}^{\mathrm{a} 1}, \mathrm{u}^{\mathrm{a} 2}\right) k⟵H(u,ua1,ua2)
- m ← D s ( k , c ) m \leftarrow D_{s}(k, c) m←Ds(k,c)
- output m
-
下面说明 twin EIGamal 的CCA security
Chosen ciphertext security
-
Security Theorem:
- If CDH holds in the group G:
- ( E s , D s ) (E_s, D_s) (Es,Ds) provides auth. enc.
- H:
G
3
→
K
G^3 \rightarrow K
G3→K is a “random oracle”
- ideal hash function (“random oracle”)
- then:
- Twin EIGamal is C C A r o CCA^{ro} CCAro secure
- If CDH holds in the group G:
-
去掉那个奇怪的假设的Cost
- One more exponentiation during enc/dec
- enc: 从2变成了3
- dec: 从1变成了2
- 这样值得吗?
- 不知道!这取决于是否存在满足上面If的那些条件(CDH, 加密认证、random oracle),但并不CCA secure的系统
- 或者说取决于是否有满足CDH但不满足IDH的groups
- 如果有的话,那就值得;否则,不值得。答案未知
- 不知道!这取决于是否存在满足上面If的那些条件(CDH, 加密认证、random oracle),但并不CCA secure的系统
- One more exponentiation during enc/dec
EIGamal security without random oracles
继续去掉random oracles!
Can we prove CCA Security without random oracles?
- Option 1: use Hash-DH assumption in “bilinear groups”
- special elliptic curve with more structure
- [CHK’04 + BB’04]
- special elliptic curve with more structure
- Option 2: Use Decision-DH assumption in any group [CS’98]
本课程不进行详细介绍,可参考论文
Further reading
- The Decision Diffie-Hellman problem, 1998
- Decision-DH assumption
- Universal hash proofs and a paradigm for chosen ciphertext secure public key encryption, 2002
- 如何使用Decision-DH assumption等建立CCA secure的公钥加密系统
- Chosen-ciphertext security from Identity-Based Encryption, 2007
- 如何从Bilinear Group中建立CCA secure的系统
- The twin Diffie-Hellman problem and applications, 2008
- twin Diffie-Hellman construction
- Efficient chosen-ciphertext security via extractable hash proofs, 2010
- a very general framework for building CCA secure systems
- using extractable hash proofs
- a very general framework for building CCA secure systems
Next segment:
- 将RSA和EIGamal统一到general principle
6.5 Public Key Encryption: Summary
6.5.1 A unifying Theme
到目前为止,见过两类public key:
- 1 RSA: 基于trapdoor function
- 2 EIGamal: 基于Diffie-Hellman
接下来:
- 说明它们其实都follow from a more general principle
One-way function
A function f : x → y f: x\rightarrow y f:x→y is one-way if
- There is an efficient algorithm to evaluate f ( cot ) f(\cot) f(cot)
- 但,Inverting f is hard
- 这里的意思是,给定y, 找到对应的原像x非常困难
- 即 for all efficient A and
x
←
X
x \leftarrow X
x←X:
- Pr[f (A(f(x))) = f(x)] < negligible
- 给定f(x) ,找到对应的原像x (满足f(A(f(x))) = f(x)),非常困难
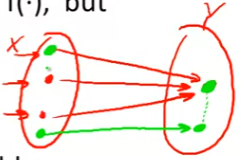
-
Functions that are not one-way:
- f(x) = x: 可逆
- f(x) = 0: 很容易找到原像: 任何x都是原像
-
(待查证)但是,证明一个函数f是one-way function非常困难
- NP 难问题
下面通过例子,以One-way function统一 public key encryption
Ex. 1: Generic one-way functions
- Let
f
:
x
→
Y
f: x\rightarrow Y
f:x→Y be a secure PRG
- where |Y| >> |X|
- e.g., f built using det. counter mode
- Lemma: f a secure PRG ⇒ \Rightarrow ⇒ f is one-way
- Proof sketch: 反证法 contra positive
- 假如A inverts f
⇒
\Rightarrow
⇒ 可构造下面的B,B能够对来自y的输入全部输出A,对于真的随机数全部输出0
- 意味着可以区分,意味着f不是a secure PRG
- 证毕!
- 因此,f是一个one-way function
- 假如A inverts f
⇒
\Rightarrow
⇒ 可构造下面的B,B能够对来自y的输入全部输出A,对于真的随机数全部输出0
- Generic: no special properties
- 但PRG没有特殊的性质,因此无法用于公钥密码学, 如key exchange
Ex 2: The DLOG one-way function
-
Fix a finite cyclic group G (e.g G = ( Z p ) ∗ ) \left.G=\left(Z_{p}\right)^{*}\right) G=(Zp)∗) of order n
-
g: a random generator in G
- i.e. G = {1,g , g 2 g^2 g2, … , g n − 1 g^{n-1} gn−1}
-
Define:
- f: Z n → G Z_n \rightarrow G Zn→G as f ( x ) = g x ∈ G f(x)=g^{x} \in G f(x)=gx∈G
-
Lemma: Dlog hard in G ⇒ \Rightarrow ⇒ f is one-way
-
Properties:
- 不同的是,离散对数满足有些性质:
- 已知f(x), f(y), 则 可计算 f(x+y) = f(x) f(y)
- ⇒ \Rightarrow ⇒ 能够被用于key-exchange 和 public-key encryption
Ex.3 The RSA one-way function
-
choose random prime p,q ≈ 1024 \approx 1024 ≈1024 bits, Set N = pq
-
choose integers e,d s.t., e ⋅ d = 1 ( m o d φ ( N ) ) e \cdot d=1(\bmod \varphi(N)) e⋅d=1(modφ(N))
-
Define: f: Z N ∗ → Z N ∗ \mathbb{Z}_{N}^{*} \rightarrow \mathbb{Z}_{N}^{*} ZN∗→ZN∗ as f ( x ) = x e f(x)=x^{e} \quad f(x)=xe in Z N \mathbb{Z}_{N} ZN
-
Lemma:
- f is one-way under the RSA assumption
- RSA assumption 就是说它是一个One-way function
- f is one-way under the RSA assumption
-
Properties:
- f ( x ⋅ y ) = f ( x ) ⋅ f ( y ) f(x \cdot y)=f(x) \cdot f(y) f(x⋅y)=f(x)⋅f(y)
- f has a trapdoor
- 这个性质使RSA能够非常方便地用于数字签名
Summary
- Public key encryption:
- 基于one-way functions with special properties!
- properties例如:
- homomorphic properties
- 给定f(x)和f(y)就能计算f(x+y)或者f(xy)
- trapdoors
- homomorphic properties
密码学2:
- 将会继续介绍数字签名
6.5.2 Farewell (For Now)
6 周课程结束,本节进行总结
Quick Review: primiteves
- Week 1: PRG
- Week 2: PRF and PRP
- Week 3: Data integrity
- MAC 各种MAC地构造
- Hash 函数
- Collision Resistance 生日悖论等
- Week 4: Authenticated Encryption
- 认证 + 加密
- Week 5: 开始一个新的topic- 公钥密码
- Trapdoor functions
- Diffie-Hellman groups
- Week 6: 具体方法
- RSA
- EIGamal
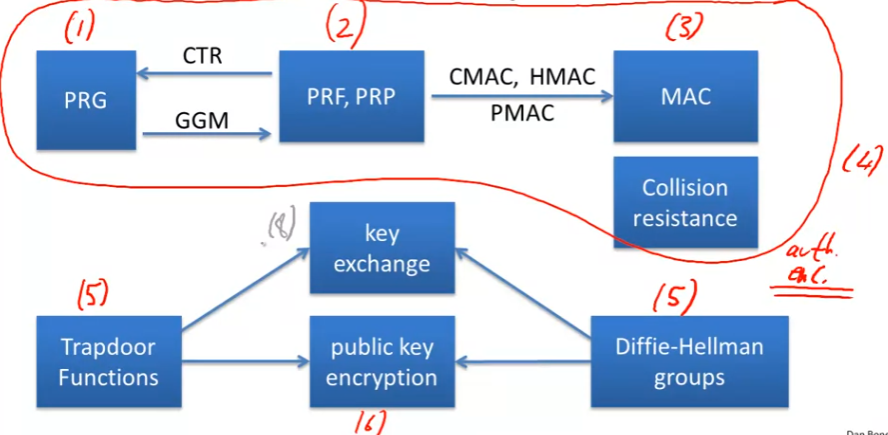
Remaining Core Topics (Part 2)
密码学2的内容包括:
- Digital signatures and certificates
- Authenticated key exchange
- User authentication
- Passwords
- one-time passwords
- challenge-response
- Privacy mechanism
- Zero-knowledge protocols
Many more topics to cover
密码学中更多的领域
- Elliptic Curve Crypto
- Quantum Computing
- New key management paradigms
- identity based encryption and functional encryption
- Anonymous digital cash
- Private voting and auction systems
- Computing on ciphertexts: fully homomorphic encryption
- Lattice-based crypto
- Two party and multi-party computation
Final Words: 不要轻易尝试使用自己实现的密码
- Be careful when using crypto
- A tramendous tool, but if incorrectly implemented:
- 系统能够工作,但可能会遭受意想不到的easy attack!
- A tramendous tool, but if incorrectly implemented:
- Make sure to have others review your designs and code
#密码学1结束























 31万+
31万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










