激光三角测量法 原理、优点和不足

目录

引言

激光三角测量法的原理

正入射

斜入射

正入射与斜入射的对比

激光三角测量法测距的特点

主要误差来源

激光抖动

被测物体表面颜色

激光光斑检测精度

入射光束的景深限制

参考文献

---

引言

激光测距是LCT等主动非视距成像的基础，因此熟悉激光测距方法还是很有必要的。激光测距主要包括干涉法、脉冲ToF法和三角测量法。本文参考几篇文献，说明激光三角测量法的原理。

 

激光三角测量法的原理

激光三角测量法的设置与双目立体视觉很像，只是将其中的一个LCD换成了laser。

激光三角测量法是利用光线空间传播过程中的光学反射规律和相似三角形原理，在接收透镜的物空间与像空间构成相似关系，同时利用边角关系计算出待测位移。根据入射激光和待测物体表面法线之间的夹角，可以将激光三角法测量分为正入射和斜入射两种情况：

正入射：入射光线与待测物体表面法线夹角为0；

斜入射：入射光线与待测物体表面法线夹角为α>0.

 

正入射

原理图如下图所示：

 

激光器发射的光束正入射到参考平面M处、测量平面N处，并分别在CCD上的M'和N'处成像，夹角等如图所示。

则根据几何光路，可知：

进而即可求解得到m.

在已知参考平面的情况下，通过m即可完成测距。

 

斜入射

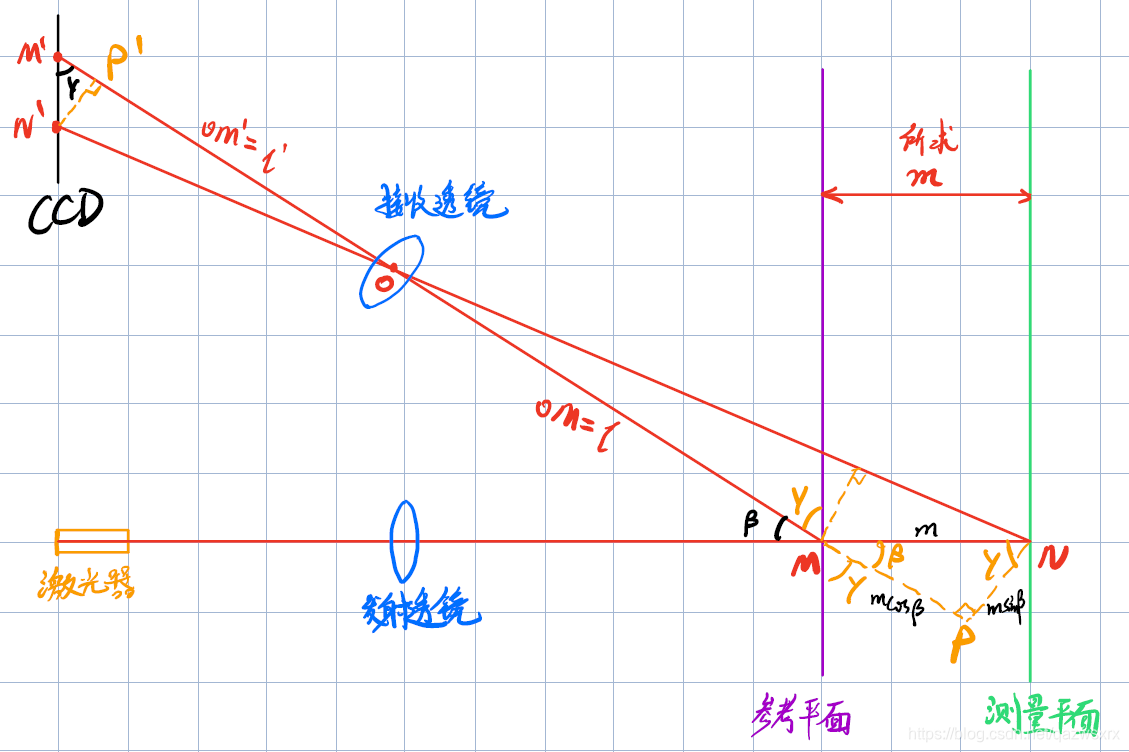
原理图如下图所示：

[注：本图有误，N点需上移，暂未更改，下述三角形相似关系和求解原理不变]

仍有三角形OPN和三角形OP‘N’相似，科得：

进而求解出m.

 

正入射与斜入射的对比

正入射：

• 可以看作是斜入射的一个特例；
• 具有更好的测量精度和测量稳定性；
• 但对复杂测量场景容易出现不适用的情况。

 

斜入射：

• 对复杂场景更易应用；
• 激光倾斜入射会导致物体表面激光光斑增大，且能量分布不均匀，导致光斑中心检测难度加大，降低检测精度；
• 斜入射的光斑位置会随位移m的改变而改变，难以完成对某固定点的测距。

激光三角测量法测距的特点

• 非接触式测距，高精度；
• 大的测量范围，对待测表面要求较低；
• 结构简单，性价比高；

 

主要误差来源

激光抖动

激光器常常会因为自身或外界原因抖动，尽管抖动角一般只有±1°，但对测量结果影响很大；

被测物体表面颜色

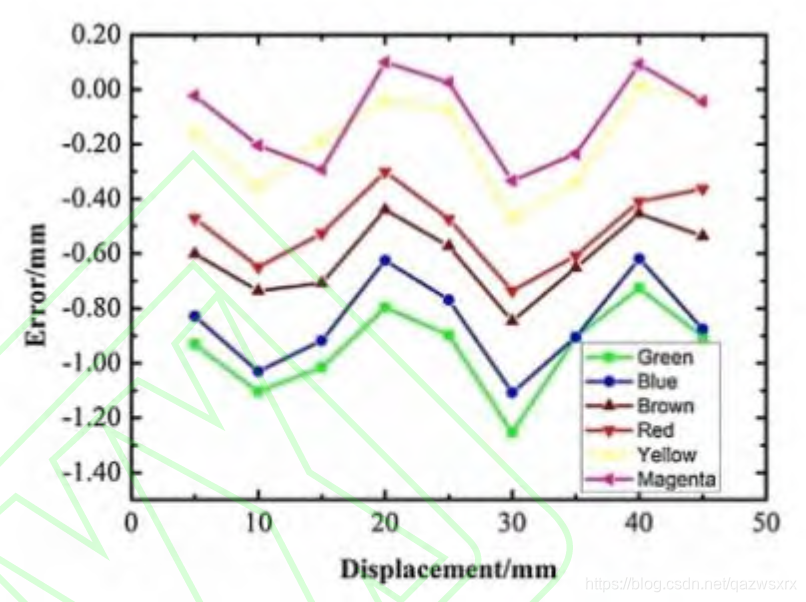
不同颜色的被测物体-->不同的反射和散射特定-->探测器CCD接收到不同的光强-->影响精度。

颜色误差测量结果如下：

激光光斑检测精度

激光光斑检测精度会对角度、l等值都会产生影响，从而影响测量精度。

入射光束的景深限制

一般的高斯光束聚焦为入射光时，会出现光斑尺寸随测量范围变大而离焦、变大的现象，使系统很难满足高分辨率和大测量范围的要求。

 

 

参考文献

[1]孙有春;庞亚军;白振旭;王雨雷;吕志伟; 激光三角测量法应用技术[J]. 激光杂志, : 1–10.

[2]https://wenku.baidu.com/view/1187afeb551810a6f524868e.html

 

==================================================================================================================

原载于 我的博客

如有错误，可联系 rxnlos@126.com

=================================================================================================================