cf708D(循环流+费用流)

最新推荐文章于 2021-09-28 11:01:04 发布

qkoqhh

最新推荐文章于 2021-09-28 11:01:04 发布

阅读量628

点赞数

分类专栏：网络流

本文链接：https://blog.csdn.net/qkoqhh/article/details/81779417

版权

网络流专栏收录该内容

34 篇文章 0 订阅

订阅专栏

这个题算是比较经典了。。

首先要解决流量不平衡的问题，这个可以用循环流解决，对于那些流量不平衡的点，分别向S和T连边获取额外的流量，然后跑满流就可以解决不平衡的问题了。。

然后对边，如果没超容量就向普通边一样连边，容量为还可以流的流量，费用为1；再设一条容量无限的边，费用为2，代表容量和流量同时更改；对流量减少的操作，可以连反向边，容量为原流量，费用为1，代表撤销操作

如果超容量，就先手动扩容量，并累加代价，这种操作可以撤销，代价为0（此时容量增加的代价转化为流量减少的代价），故连反向边，容量为超容量的部分，费用为0；然后其他的像上面一样，连正向费用为2的边和连方向费用为1的边。。

建图方式还是非常骚的。。还是要花点时间理解。。

/**
 *　　　　　　  　　┏┓　　 　┏┓
 * 　　　　　  　　┏┛┗━━━━━━━┛┗━━━┓
 * 　　　　　  　　┃　　　　　　　┃ 　
 * 　　　　　  　　┃　　　━　　 　┃
 * 　　　　　  　　┃　＞　　　＜　┃
 * 　　　　　  　　┃　　　　　　　┃
 * 　　　　　  　　┃...　⌒　... 　┃
 * 　　　　　　  　┃              ┃
 * 　　　　　　  　┗━┓          ┏━┛
 * 　　　　　　　　　┃          ┃　Code is far away from bug with the animal protecting　　　　　　　　　　
 * 　　　　　　　　　┃          ┃   神兽保佑,代码无bug
 * 　　　　　　　　　┃          ┃　　　　　　　　　　　
 * 　　　　　　　　　┃          ┃  　　　　　　
 * 　　　　　　　　　┃          ┃
 * 　　　　　　　　　┃          ┃　　　　　　　　　　　
 * 　　　　　　　　　┃          ┗━━━┓
 * 　　　　　　　　　┃              ┣┓
 * 　　　　　　　　　┃              ┏┛
 * 　　　　　　　　　┗┓┓┏━━━━━━━━┳┓┏┛
 * 　　　　　　　　　　┃┫┫       ┃┫┫
 * 　　　　　　　　　　┗┻┛       ┗┻┛
 */
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<queue>
#include<cmath>
#include<map>
#include<stack>
#include<set>
#include<bitset>
#include<assert.h>
#define inc(i,l,r) for(int i=l;i<=r;i++)
#define dec(i,l,r) for(int i=l;i>=r;i--)
#define link(x) for(edge *j=h[x];j;j=j->next)
#define mem(a) memset(a,0,sizeof(a))
#define ll long long
#define eps 1e-8
#define succ(x) (1LL<<(x))
#define lowbit(x) (x&(-x))
#define sqr(x) ((x)*(x))
#define mid (x+y>>1)
#define NM 200005
#define nm 400005 
#define N 1000005
#define M(x,y) x=max(x,y)
const double pi=acos(-1);
const int inf=998244353;
using namespace std;
ll read(){
    ll x=0,f=1;char ch=getchar();
    while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
    while(isdigit(ch))x=x*10+ch-'0',ch=getchar();
    return f*x;
}



struct edge{int t,v,w;edge*next,*rev;}e[nm],*h[NM],*o=e,*p[NM];
void _add(int x,int y,int w,int v){o->t=y;o->v=v;o->w=w;o->next=h[x];h[x]=o++;}
void add(int x,int y,int w,int v){_add(x,y,w,v);_add(y,x,0,-v);h[x]->rev=h[y];h[y]->rev=h[x];}
int n,m,_x,_y,_v,_t,a[NM],d[NM],b[NM],ans;
bool v[NM];
queue<int>q;


int spfa(){
    inc(i,1,n)d[i]=inf;mem(b);
    q.push(0);b[0]=inf;d[0]=0;v[0]++;
    while(!q.empty()){
	int t=q.front();q.pop();v[t]=false;
	link(t)if(j->w&&d[j->t]>d[t]+j->v){
	    d[j->t]=d[t]+j->v;p[j->t]=j;b[j->t]=min(b[t],j->w);
	    if(!v[j->t])q.push(j->t),v[j->t]++;
	}
    }
    return b[n];
}

int main(){
    n=read();m=read();
    inc(i,1,m){
	_x=read();_y=read();_v=read();_t=read();
	a[_x]-=_t;a[_y]+=_t;
	if(_v>=_t){
	    add(_x,_y,_v-_t,1);
	    add(_x,_y,inf,2);
	    add(_y,_x,_t,1);
	}else{
	    ans+=_t-_v;
	    add(_y,_x,_t-_v,0);
	    add(_y,_x,_v,1);
	    add(_x,_y,inf,2);
	}
    }
    add(n,1,inf,0);
    inc(i,1,n)if(a[i]>0)add(0,i,a[i],0);else if(a[i]<0)add(i,n+1,-a[i],0);
    n++;
    while(spfa()){
	ans+=b[n]*d[n];
	for(int x=n;x;x=p[x]->rev->t)p[x]->w-=b[n],p[x]->rev->w+=b[n];
    }
    return 0*printf("%d\n",ans);
}

D. Incorrect Flow

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

At the entrance examination for the magistracy of the MSU Cyber-Mechanics Department Sasha got the question about Ford-Fulkerson algorithm. He knew the topic perfectly as he worked with it many times on programming competition. As the task for the question he was given a network with partially build flow that he had to use in order to demonstrate the workflow of the algorithm. He quickly finished to write the text and took a look at the problem only to understand that the given network is incorrect!

Suppose you are given a directed graph G(V, E) with two special nodes s and t called source and sink. We denote as n the number of nodes in the graph, i.e. n = |V| and m stands for the number of directed edges in the graph, i.e. m = |E|. For the purpose of this problem we always consider node 1 to be the source and node n to be the sink. In addition, for each edge of the graph e we define the capacity function c(e) and flow function f(e). Function f(e) represents the correct flow if the following conditions are satisfied:

For each edge 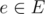the flow is non-negative and does not exceed capacity c(e), i.e. 0 ≤ f(e) ≤ c(e).
For each node 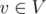, that is not source or sink (v ≠ s and v ≠ t) the sum of flows of all edges going in v is equal to the sum of the flows among all edges going out from v. In other words, there is no flow stuck in v.

It was clear that as the exam was prepared last night and there are plenty of mistakes in the tasks. Sasha asked one of the professors to fix the network or give the correct task, but the reply was that the magistrate student should be able to fix the network himself. As the professor doesn't want the task to become easier, he asks Sasha to fix the network in a such way that the total number of changes is minimum possible. Sasha is not allowed to remove edges, add new ones or reverse the direction of existing edges. The only thing he is able to do is to change capacity function c(e) and flow function f(e). Moreover, all the values should remain non-negative integers. There is no requirement on the flow to be maximum in any sense.

Find the minimum possible total change of the functions f(e) and c(e) that Sasha has to make in order to make the flow correct. The total change is defined as the sum of absolute differences, i.e. if new functions are f * (e) and c * (e), then the total change is .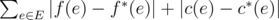

Input

The first line of the input contains two integers n and m (2 ≤ n ≤ 100, 0 ≤ m ≤ 100) — the number of nodes and edges in the graph respectively. Each of the following m lines contains the description of the edges, consisting of four integers ui, vi, ci and fi (1 ≤ ui, vi ≤ n, ui ≠ vi, 0 ≤ ci, fi ≤ 1 000 000) — index of the node the edges starts from, the index of the node the edge goes to, current capacity and flow value.

Node number 1 is the source, and node number n is the sink. It's guaranteed that no edge goes to the source, and no edges starts in the sink.

Given graph contains no self-loops but may contain multiple edges.

Output

Print one integer — the minimum total sum of changes that Sasha has to do in order to get the correct flow description.

Examples

Input

Copy

2 1
1 2 2 1

Output

Copy

Input

Copy

2 1
1 2 1 2

Output

Copy

Input

Copy

Output

Copy

Input

Copy

4 2
2 3 1 1
3 2 1 1

Output

Copy

Note

In the first sample, the flow is initially correct. Note, that the flow is not maximum, but this is not required.

In the second sample, the flow value of the only edge is greater than its capacity. There are two ways to fix this: either increase the capacity up to 2 or reduce the flow down to 1.

In the third sample, there is only 1 unit of flow coming to vertex 2, but there are 2 units going out of it. One of the possible solutions is to reduce the value of the flow on the second edge by 1.

In the fourth sample, there is isolated circulation of flow, but this description is correct by definition.