我们最终所需要的算法名字是:Contrast Limited Adaptive Histogram Equalization限制对比度自适应直方图均衡化,每个单词取首字母可以缩写为:CLAHE
直方图的原理以及作用可以参考这里,总之就是,算最终的均衡化是经历过计算直方图以及累积分布直方图两个过程,其理论基础在参考的文献里解释的非常清楚.但是从原始的HE到CLAHE中间经历了多个优化算法,网上很少有直观的代码实现,好不容易在这篇文章里找到.下面的介绍主要是结合代码,进行部分解释说明.
直方图均衡化,HE:
这个是最基础版本,代码表现的很清楚
Mat eaualizeHist_GO(Mat src){
int width = src.cols;
int height= src.rows;
Mat HT_GO = src.clone();
int tmp[256] ={0};
float C[256] = {0.0};
int total = width*height;
for (int i=0 ;i<src.rows;i++){
for (int j=0;j<src.cols;j++){
int index = src.at<uchar>(i,j);
tmp[index] ++;
}
}
//计算累积函数
for(int i = 0;i < 256 ; i++){
if(i == 0)
C[i] = 1.0f * tmp[i] / total;
else
C[i] = C[i-1] + 1.0f * tmp[i] / total;
}
//这里的累积函数分配的方法非常直观高效
for(int i = 0;i < src.rows;i++){
for(int j = 0;j < src.cols;j++){
int index = src.at<uchar>(i,j);
HT_GO.at<uchar>(i,j) = C[index] * 255 ;
}
}
return HT_GO;
}自适应直方图均衡化,AHE:
把整个大图分成8X8=64份,当然,这里的举例图像的长宽正好是8的倍数.写入到存储直方图的数组的顺序是按照没一行的从左到右, 一共八行.
Mat aheGO(Mat src,int _step = 8){
Mat AHE_GO = src.clone();
int block = _step;
int width = src.cols;
int height = src.rows;
int width_block = width/block; //每个小格子的长和宽
int height_block = height/block;
//存储各个直方图
int tmp2[8*8][256] ={0};
float C2[8*8][256] = {0.0};
//分块
int total = width_block * height_block;
for (int i=0;i<block;i++){
for (int j=0;j<block;j++){
int start_x = i*width_block;
int end_x = start_x + width_block;
int start_y = j*height_block;
int end_y = start_y + height_block;
int num = i+block*j;
//遍历小块,计算直方图
for(int ii = start_x ; ii < end_x ; ii++) {
for(int jj = start_y ; jj < end_y ; jj++) {
int index =src.at<uchar>(jj,ii);
tmp2[num][index]++;
}
}
//计算累积分布直方图
for(int k = 0 ; k < 256 ; k++){
if( k == 0)
C2[num][k] = 1.0f * tmp2[num][k] / total;
else
C2[num][k] = C2[num][k-1] + 1.0f * tmp2[num][k] / total;
}
}
}
//将统计结果写入
for (int i=0;i<block;i++){
for (int j=0;j<block;j++){
int start_x = i*width_block;
int end_x = start_x + width_block;
int start_y = j*height_block;
int end_y = start_y + height_block;
int num = i+block*j;
//遍历小块,计算直方图
for(int ii = start_x ; ii < end_x ; ii++){
for(int jj = start_y ; jj < end_y ; jj++){
int index =src.at<uchar>(jj,ii);
//结果直接写入AHE_GO中去
AHE_GO.at<uchar>(jj,ii) = C2[num][index] * 255 ;
}
}
}
}
return AHE_GO;
}限制对比度直方图均衡化:CLHE.
对比度指的是一副图片中最亮的白和最暗的黑之间的反差大小=(max-min)/(max+min).对比度增强可以使用线性拉伸的方式,即,直接将(min1,max1)的范围扩大到(min2,max2).但是对于比较复杂的图片没有什么效果.直方图均衡化,也是一种拉伸对比度的方式.
HE算法在一种情况下,效果不好,如果一个图片中有大块的暗区或者亮区的话,效果非常不好。这个的原因,也非常好理解,因为HE其实要求一个图片中必须有10%的最亮的像素点,必须有10%第二亮的像素点,必须有10%第三亮的像素点……假设有一张纯黑的图片,你想想经过HE处理之后,会出现什么情况?答案就是一部分黑的像素也会被强行搞成白的.来自.
因此单纯的直方图均衡化,AH比较适合一副图像整体偏暗或者亮.如果局部有个比较亮或者暗的,就会多出很多干扰信息.因此进行对比度限制,可以减弱带来的不利影响.

主要体现在:
假如左图为原图的直方图,在计算累积函数的时候,先转换成右图.这样可以达到限制对比度的功能.即进行削峰,并将削下来的量均匀的分配给每个色阶(或者亮度值).
Mat clheGO(Mat src,int _step = 8)
{
int width = src.cols;
int height= src.rows;
Mat CLHE_GO = src.clone();
int tmp[256] ={0};
float C[256] = {0.0};
int total = width*height;
for (int i=0 ;i<src.rows;i++){
for (int j=0;j<src.cols;j++){
int index = src.at<uchar>(i,j);
tmp[index] ++;
}
}
/限制对比度计算部分,注意这个地方average的计算不一定科学
int average = width * height / 255/64;
int LIMIT = 4 * average;
int steal = 0;
for(int k = 0 ; k < 256 ; k++){
if(tmp[k] > LIMIT){
steal += tmp[k] - LIMIT;
tmp[k] = LIMIT;
}
}
int bonus = steal/256;
//hand out the steals averagely
for(int k = 0 ; k < 256 ; k++){
tmp[k] += bonus;
}
///
//计算累积函数
for(int i = 0;i < 256 ; i++){
if(i == 0)
C[i] = 1.0f * tmp[i] / total;
else
C[i] = C[i-1] + 1.0f * tmp[i] / total;
}
//这里的累积函数分配的方法非常直观高效
for(int i = 0;i < src.rows;i++){
for(int j = 0;j < src.cols;j++){
int index = src.at<uchar>(i,j);
CLHE_GO.at<uchar>(i,j) = C[index] * 255 ;
}
}
return CLHE_GO;
}
CLAHE
将上面的AHE结合就是不带有插值算法的CLAHE:
Mat claheGoWithoutInterpolation(Mat src, int _step = 8)
{
Mat CLAHE_GO = src.clone();
int block = _step;//pblock
int width = src.cols;
int height= src.rows;
int width_block = width/block; //每个小格子的长和宽
int height_block = height/block;
//存储各个直方图
int tmp2[8*8][256] ={0};
float C2[8*8][256] = {0.0};
//分块
int total = width_block * height_block;
for (int i=0;i<block;i++){
for (int j=0;j<block;j++){
int start_x = i*width_block;
int end_x = start_x + width_block;
int start_y = j*height_block;
int end_y = start_y + height_block;
int num = i+block*j;
//遍历小块,计算直方图
for(int ii = start_x ; ii < end_x ; ii++){
for(int jj = start_y ; jj < end_y ; jj++){
int index =src.at<uchar>(jj,ii);
tmp2[num][index]++;
}
}
//裁剪和增加操作,也就是clahe中的cl部分
//这里的参数 对应《Gem》上面 fCliplimit = 4 , uiNrBins = 255
int average = width_block * height_block / 255;
int LIMIT = 4 * average;
int steal = 0;
for(int k = 0 ; k < 256 ; k++){
if(tmp2[num][k] > LIMIT){
steal += tmp2[num][k] - LIMIT;
tmp2[num][k] = LIMIT;
}
}
int bonus = steal/256;
//hand out the steals averagely
for(int k = 0 ; k < 256 ; k++){
tmp2[num][k] += bonus;
}
//计算累积分布直方图
for(int k = 0 ; k < 256 ; k++){
if( k == 0)
C2[num][k] = 1.0f * tmp2[num][k] / total;
else
C2[num][k] = C2[num][k-1] + 1.0f * tmp2[num][k] / total;
}
}
}
//计算变换后的像素值
//将统计结果写入
for (int i=0;i<block;i++){
for (int j=0;j<block;j++){
int start_x = i*width_block;
int end_x = start_x + width_block;
int start_y = j*height_block;
int end_y = start_y + height_block;
int num = i+block*j;
//遍历小块,计算直方图
for(int ii = start_x ; ii < end_x ; ii++){
for(int jj = start_y ; jj < end_y ; jj++){
int index =src.at<uchar>(jj,ii);
//结果直接写入AHE_GO中去
CLAHE_GO.at<uchar>(jj,ii) = C2[num][index] * 255 ;
}
}
}
}
return CLAHE_GO;
}这样的结果会有严重的网格感觉,需要使用插值的方式进行解决:
Mat claheGO(Mat src,int _step = 8)
{
Mat CLAHE_GO = src.clone();
int block = _step;//pblock
int width = src.cols;
int height= src.rows;
int width_block = width/block; //每个小格子的长和宽
int height_block = height/block;
//存储各个直方图
int tmp2[8*8][256] ={0};
float C2[8*8][256] = {0.0};
//分块
int total = width_block * height_block;
for (int i=0;i<block;i++)
{
for (int j=0;j<block;j++)
{
int start_x = i*width_block;
int end_x = start_x + width_block;
int start_y = j*height_block;
int end_y = start_y + height_block;
int num = i+block*j;
//遍历小块,计算直方图
for(int ii = start_x ; ii < end_x ; ii++)
{
for(int jj = start_y ; jj < end_y ; jj++)
{
int index =src.at<uchar>(jj,ii);
tmp2[num][index]++;
}
}
//裁剪和增加操作,也就是clahe中的cl部分
//这里的参数 对应《Gem》上面 fCliplimit = 4 , uiNrBins = 255
int average = width_block * height_block / 255;
//关于参数如何选择,需要进行讨论。不同的结果进行讨论
//关于全局的时候,这里的这个cl如何算,需要进行讨论
int LIMIT = 40 * average;
int steal = 0;
for(int k = 0 ; k < 256 ; k++)
{
if(tmp2[num][k] > LIMIT){
steal += tmp2[num][k] - LIMIT;
tmp2[num][k] = LIMIT;
}
}
int bonus = steal/256;
//hand out the steals averagely
for(int k = 0 ; k < 256 ; k++)
{
tmp2[num][k] += bonus;
}
//计算累积分布直方图
for(int k = 0 ; k < 256 ; k++)
{
if( k == 0)
C2[num][k] = 1.0f * tmp2[num][k] / total;
else
C2[num][k] = C2[num][k-1] + 1.0f * tmp2[num][k] / total;
}
}
}
//计算变换后的像素值
//根据像素点的位置,选择不同的计算方法
for(int i = 0 ; i < width; i++)
{
for(int j = 0 ; j < height; j++)
{
//four coners
if(i <= width_block/2 && j <= height_block/2)
{
int num = 0;
CLAHE_GO.at<uchar>(j,i) = (int)(C2[num][CLAHE_GO.at<uchar>(j,i)] * 255);
}else if(i <= width_block/2 && j >= ((block-1)*height_block + height_block/2)){
int num = block*(block-1);
CLAHE_GO.at<uchar>(j,i) = (int)(C2[num][CLAHE_GO.at<uchar>(j,i)] * 255);
}else if(i >= ((block-1)*width_block+width_block/2) && j <= height_block/2){
int num = block-1;
CLAHE_GO.at<uchar>(j,i) = (int)(C2[num][CLAHE_GO.at<uchar>(j,i)] * 255);
}else if(i >= ((block-1)*width_block+width_block/2) && j >= ((block-1)*height_block + height_block/2)){
int num = block*block-1;
CLAHE_GO.at<uchar>(j,i) = (int)(C2[num][CLAHE_GO.at<uchar>(j,i)] * 255);
}
//four edges except coners
else if( i <= width_block/2 )
{
//线性插值
int num_i = 0;
int num_j = (j - height_block/2)/height_block;
int num1 = num_j*block + num_i;
int num2 = num1 + block;
float p = (j - (num_j*height_block+height_block/2))/(1.0f*height_block);
float q = 1-p;
CLAHE_GO.at<uchar>(j,i) = (int)((q*C2[num1][CLAHE_GO.at<uchar>(j,i)]+ p*C2[num2][CLAHE_GO.at<uchar>(j,i)])* 255);
}else if( i >= ((block-1)*width_block+width_block/2)){
//线性插值
int num_i = block-1;
int num_j = (j - height_block/2)/height_block;
int num1 = num_j*block + num_i;
int num2 = num1 + block;
float p = (j - (num_j*height_block+height_block/2))/(1.0f*height_block);
float q = 1-p;
CLAHE_GO.at<uchar>(j,i) = (int)((q*C2[num1][CLAHE_GO.at<uchar>(j,i)]+ p*C2[num2][CLAHE_GO.at<uchar>(j,i)])* 255);
}else if( j <= height_block/2 ){
//线性插值
int num_i = (i - width_block/2)/width_block;
int num_j = 0;
int num1 = num_j*block + num_i;
int num2 = num1 + 1;
float p = (i - (num_i*width_block+width_block/2))/(1.0f*width_block);
float q = 1-p;
CLAHE_GO.at<uchar>(j,i) = (int)((q*C2[num1][CLAHE_GO.at<uchar>(j,i)]+ p*C2[num2][CLAHE_GO.at<uchar>(j,i)])* 255);
}else if( j >= ((block-1)*height_block + height_block/2) ){
//线性插值
int num_i = (i - width_block/2)/width_block;
int num_j = block-1;
int num1 = num_j*block + num_i;
int num2 = num1 + 1;
float p = (i - (num_i*width_block+width_block/2))/(1.0f*width_block);
float q = 1-p;
CLAHE_GO.at<uchar>(j,i) = (int)((q*C2[num1][CLAHE_GO.at<uchar>(j,i)]+ p*C2[num2][CLAHE_GO.at<uchar>(j,i)])* 255);
}
//双线性插值
else{
int num_i = (i - width_block/2)/width_block;
int num_j = (j - height_block/2)/height_block;
int num1 = num_j*block + num_i;
int num2 = num1 + 1;
int num3 = num1 + block;
int num4 = num2 + block;
float u = (i - (num_i*width_block+width_block/2))/(1.0f*width_block);
float v = (j - (num_j*height_block+height_block/2))/(1.0f*height_block);
CLAHE_GO.at<uchar>(j,i) = (int)((u*v*C2[num4][CLAHE_GO.at<uchar>(j,i)] +
(1-v)*(1-u)*C2[num1][CLAHE_GO.at<uchar>(j,i)] +
u*(1-v)*C2[num2][CLAHE_GO.at<uchar>(j,i)] +
v*(1-u)*C2[num3][CLAHE_GO.at<uchar>(j,i)]) * 255);
}
//最后这步,类似高斯平滑
CLAHE_GO.at<uchar>(j,i) = CLAHE_GO.at<uchar>(j,i) + (CLAHE_GO.at<uchar>(j,i) << 8) + (CLAHE_GO.at<uchar>(j,i) << 16);
}
}
return CLAHE_GO;
}插值的方式就是根据一个点周围四个点的值来确定.只是说其值为累积分布直方图的值.分成64个块.每个块又分成四个小块.整个图像的四个顶点所在的小块不用插值.除此之外的四个边采用'单'线性插值.剩下的为双线性插值.因此可以简单的理解为,只有相邻的小块才会进行插值.
整体来讲上面遗留了两个问题:
int average = width_block * height_block / 255;
int LIMIT = 40 * average;
int steal = 0; 1、在进行CLAHE中CL的计算,也就是限制对比度的计算的时候,参数的选择缺乏依据。在原始的《GEMS》中提供的参数中, fCliplimit = 4 , uiNrBins = 255.但是在OpenCV的默认参数中,这里是40.就本例而言,如果从结果上反推,我看10比较好。这里参数的选择缺乏依据;
2、CLHE是可以用来进行全局直方图增强的,那么这个时候,这个average 如何计算,肯定不是width * height/255,这样就太大了,算出来的LIMIT根本没有办法获得。
优化
该博主的图像处理系列很值得细细品味。这里也结合他对直方图均衡化系列的文章,提取出比较新颖的观点进行总结。
一:三通道联合处理:
for (Y = 0; Y < Height; Y++){
Pointer = Scan0 + Y * Stride; // 定位到每个扫描行的第一个像素,以避免溶于数据的影响
for (X = 0; X < Width; X++){
HistGram[*Pointer]++; // Blue
HistGram[*(Pointer + 1)]++; // Green
HistGram[*(Pointer + 2)]++; // Red
Pointer += 3; // 移向下一个像素
}
}
Num = 0;
for (Y = 0; Y < 256; Y++){
Num = Num + HistGram[Y];
Lut[Y] = (byte)((float)Num / (Width * Height * 3) * 255); // 计算映射表
}
for (Y = 0; Y < Height; Y++){
Pointer = Scan0 + Y * Stride;
for (X = 0; X < Width * 3; X += 3){
Pointer[X] = Lut[Pointer[X]];
Pointer[X + 1] = Lut[Pointer[X + 1]];
Pointer[X + 2] = Lut[Pointer[X + 2]];
}
}二:强化的基于局部直方图裁剪均衡化的对比度调节算法
比如说该篇中除了提到了局部直方图和全局直方图以及亮度分量的融合方法,也对累积分布直方图中(局部均衡化后映射表)的平滑思想做了介绍:
第一种思想就是,将色阶(bins,比如256)均匀分成K(比如说是32)份,每份的开始的值和索引(原始像素值)构成二维序列点。这样根据这K个点可以拟合出一条平滑曲线。这个曲线插值成离散的后即可成为新的映射表。这样的累积分布直方图就会更加的平滑。
第二种思想就是,将映射表(累计分布直方图)中的值,进行一维的均值或者高斯滤波,同样也可以达到平滑的作用。
三:自动色阶
这篇是基于自动色阶的算法来实现的图像增强,首先,自动色阶是另外一种裁剪直方图的方式,通过设置lowcut和highcut两个参数来确定裁剪直方图两头的程度,裁剪的两端设置为极端值(比如说0或者1),中间的在重新映射到0-1(0-255)的范围,使像素值进行拉伸(可以线性,即拉伸时的系数为1,也可以gamma曲线的方式),从而达到对比度增强的效果。
# 裁剪
PixelAmount = Width * Height '所有像素的数目
Sum = 0
For Y = 0 To 255
Sum = Sum + HistBlue(Y)
If Sum >= PixelAmount * LowCut * 0.01 Then '注意PS界面里的那个百分号
MinBlue = Y '得到蓝色分量的下限
Exit For '退出循环
End If
Next
Sum = 0
For Y = 255 To 0 Step -1
Sum = Sum + HistBlue(Y)
If Sum >= PixelAmount * HighCut * 0.01 Then '注意PS界面里的那个百分号
MaxBlue = Y '得到蓝色分量的上限
Exit For '退出循环
End If
Next
# 映射
For Y = 0 To 255
If Y <= MinBlue Then
BlueMap(Y) = 0
ElseIf Y >= MaxBlue Then
BlueMap(Y) = 255
Else
BlueMap(Y) = (Y - MinBlue) / (MaxBlue - MinBlue) * 255 '线性映射
End If
Next自动对比度与自动色阶稍有不同的地方是自动色阶各通道(对于多通道,如果是灰度图这种单通道,两者算法一样),动对比度算法首先获取三个通道下限值的最小值,以及上限值的最大值,然后以此为新的上下限,计算映射表。
上面提到,在拉伸过程中,也可以使用gamma矫正的方式,即在这里:
((Y - Min) / (Max - Min)) * 255
线性拉伸为1,gamma的方式可以为:
pow((float)(Y - Min) / (Max - Min), Gamma) * 255
gamma的值可以根据如下求得:
float Avg = 0, Mean = 0, Sum = 0;
for (int Y = 0; Y < 256; Y++)
{
Sum += Histgram[Y];
Avg += Y * Histgram[Y];
}
Mean = Avg / Sum;
float Gamma = log(0.5f) / log((float)(Mean - Min) / (Max - Min));
if (Gamma < 0.1f)
Gamma = 0.1f;
else if (Gamma > 10)
Gamma = 10;局部自适应自动色阶除了上面介绍的自动色阶方法还结合了CLAHE,当然这里的自适应限制对比度直方图均衡话中的限制就不需要了,因为限制也是一种裁剪方式。在计算最后的裁剪位置后,还可以通过设置一个参数来进行调整对比度的程度。
void MakeMapping(int* Histgram,float CutLimit=0.01,float Contrast = 1){
int I, Sum = 0, Amount = 0;
const int Level = 256;
for (I = 0; I < Level; I++) Amount += Histgram[I];
int MinB =0 ,MaxB=255;
int Min = 0,Max=255;
for (I = 0; I < Level; I++){
if (Histgram[I]!=0){
Min = I ;
break;}
}
for(I = Level-1; I >= 0; I--){
if (Histgram[I]!=0){
Max = I ;
break;}
}
for (I = 0; I < Level; I++){
Sum = Sum + Histgram[I];
if (Sum >= Amount * CutLimit){
MinB = I;
break;}
}
Sum = 0;
for(I = Level-1; I >= 0; I--){
Sum = Sum +Histgram[I];
if (Sum >= Amount * CutLimit ){
MaxB = I ;
break;}
}
int Delta = (Max - Min) * Contrast * 0.5 ;
Min = Min - Delta;
Max = Max + Delta ;
if (Min < 0) Min = 0;
if (Max > 255) Max = 255;
if (MaxB!=MinB){
for (I = 0; I < Level; I++){
if (I<MinB) Histgram[I] =Min;
else if(I>MaxB) Histgram[I]=Max;
else
Histgram[I] = (Max-Min)* (I - MinB) / (MaxB - MinB) + Min ;
}
}
else{
for (I = 0; I < Level; I++) Histgram[I]=MaxB; // 必须有,不然会有一些图像平坦的部位效果出错
}
}图像增强
整理上面提到博主的一些其他图像增强的方法。
这里提到的增强平时常用的一种锐化方法,过程即是将图像分为高低频,然后高频部分的乘以一个大于1的系数。这样得到的原图的边缘部分就会放大,达到了锐化或对比度增强的效果。

系数的选择可以使用动态的方法,这样可以避免某些地方过大的锐化造成的震铃现象。D可以使用全局平均值或者全局均方差。
这里提到的是(多尺度视网膜增强算法)MSRCR的色彩增强算法。主要是根据下面的公式来:
Log[R(x,y)] = Log[I(x,y)]-Log[L(x,y)]
I是原始图像,R是增强后的图像,L为原图经过高斯或者均值模糊后的图片。后面提到的尺度也就是模糊核的半径。
通过上式反推出R,即增强后的图像。文章中提到的量化算法比较新颖。本来求解中涉及到的log函数需要通过exp才能的出R,但是可以通过求解log[R(x,y)](value)的最大(max)最小(min)值后,线性方法的方式得到量化结果。不知道为什么这样做,难道只是为了提速?
R(x,y) = ( Value - Min ) / (Max - Min) * (255-0)
所谓的多尺度就是进行多个尺度的模糊,然后进行权重求和。
Log[R(x,y)] = Log[R(x,y)] + Weight(i)* ( Log[Ii(x,y)]-Log[Li(x,y)])
其中Weight(i)表示每个尺度对应的权重,要求各尺度权重之和必须为1,经典的取值为等权重。
但是,SSR(单尺度)和MSR(多尺度)在最大尺度相同的时候效果谁好谁坏不太好说。
这种方式会导致色差,解决的方式一般可以通过一下过程:
(1)分别计算出 Log[R(x,y)]中R/G/B各通道数据的均值Mean和均方差Var(注意是均方差)。
(2)利用类似下述公式计算各通道的Min和Max值。
Min = Mean - Dynamic * Var;
Max = Mean + Dynamic * Var;
(3) 对Log[R(x,y)]的每一个值Value,进行线性映射:
R(x,y) = ( Value - Min ) / (Max - Min) * (255-0) ,同时要注意增加一个溢出判断,即:
if (R(x,y) > 255) R(x,y) =255; else if (R(x,y) < 0) R(x,y)=0;Dynamic取值越小,图像的对比度月想,一般为2-3能取得比较好的效果。
这里是一种gamma矫正的方式进习惯你对比度增强的算法。主要是进行一个动态的gamma值。使得小于128的像素使用gamma值为0-1的范围,从而使原来的元素值变大。反之,亦然。并且距离中心128越远,gamma值的变化会越剧烈。
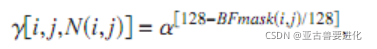

其中,BFmask是双边滤波或者均值滤波模糊后的图像。 α一般取2。也可以动态矫正,比如说,对于低对比度的图像,应该需要较强烈的校正,因此α值应该偏大,而对于有较好对比度的图,α值应该偏向于1,从而产生很少的校正量。
对于三种通道RGB的的处理方式,除了三通道分别处理外,也可以使用如下方式:
一:原图转换到YUV或者HSV这中带亮度的颜色空间中,然后用新得到的luminance值代替Y通道或V通道,然后在转换会RGB空间
二:新的luminance值和原始luminance值的比值作为三通到的增强系数,这样三通道可以得到同样程度的增强。
三:可以根据该公式:

第一种方法容易出现结果图色彩偏淡,第二种每个分量易出现过饱和,第三种可能要稍微好一点,建议使用第三种。
























 9096
9096

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








