平滑滤波是光谱分析中常用的预处理方法之一。用Savitzky.Golay方法进行平滑滤波,可以提高光谱的平滑性,并降低噪音的干扰。S-G平滑滤波的效果,随着选取窗宽不同而不同,可以满足多种不同场合的需求。
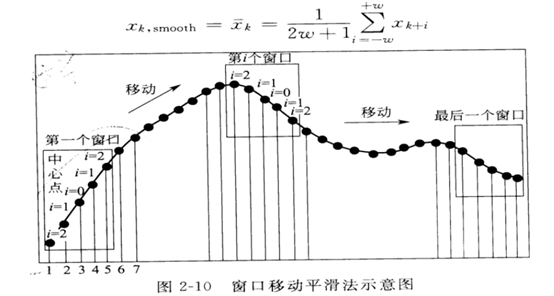
Savitzky-Golay卷积平滑算法是移动平滑算法的改进。
每一测量值以平滑系数的目的是尽可能减少平滑对有用信息的影响,该烧平滑去噪算法的劣势,可基于最小二乘原理,用于多项式拟合求的。
Savitzky-Golay卷积平滑关键在于矩阵算子的求解。
设滤波窗口的宽度为n=2m+1,各测量点为x=(-m,-m+1,0,,,,0,1,…m-1,m)采用k-1次多项式对窗口内的数据点进行拟合
于是就有了n个这样的方程,扣成了k元线性方程组。要使方程组有解则n应大于等于k,一般选择n>k,通过最小二乘法拟合确定拟合参数A。由此得到
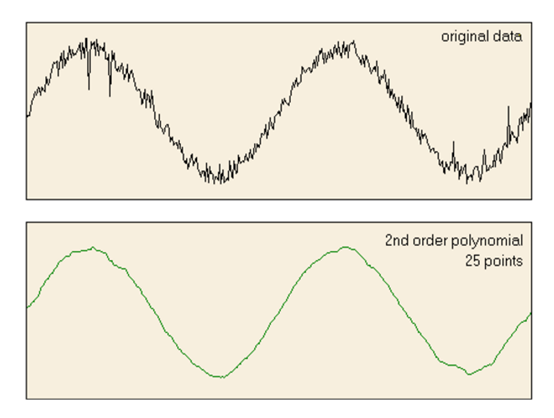
最后我自己得到的效果不是很明显,因为曲线本身的噪声不多,所以借用一张很清晰的曲线来表达,这个效果更让人接受。








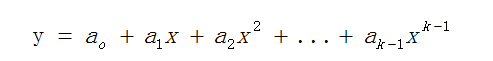

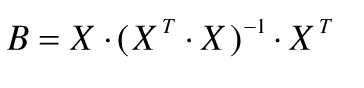
















 497
497

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








