地图投影中的墨卡托投影

地图投影中的墨卡托投影

1、基础和定义

• $R$ 地球半径
• 弧长公式 $l=R\alpha$

2、地图投影的定义

地图投影: 一种将球面上的点转换为平面上的点的方法。

目标是建立平面上的点(平面直角坐标系)和球面上的点(经纬度)之间的函数关系。
$$\begin{gathered} x=f1(\varphi ,\gamma ) \\ y=f2(\varphi ,\gamma ) \end{gathered}$$

2、地图投影变形

投影变形分为: 长度变形, 面积变形, 角度变形。

1) 长度变形

$$长度比:\mu =d{s}^{\prime }/ds=\frac{A^{\prime }{B}^{\prime }}{AB}$$

2) 面积变形

$$面积比:P=d{F}^{\prime }/dF=\frac{S_{A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }}}{S_{ABCD}}$$

3) 角度变形
$$\begin{array}{rl}\Delta u& =\mu -{\mu }^{\prime }\\ & =(180-2\alpha )-(180-2{\alpha }^{\prime })\\ & =2(\alpha -{\alpha }^{\prime })\end{array}$$

A点的坐标为(x, y)
A’点的坐标为(x’, y’)

$$tan\alpha =\frac{y}{x},tan{\alpha }^{\prime }=\frac{y^{\prime }}{x^{\prime }}$$

a极大经度长度比, b极大纬度长度比,有:
$$a=\frac{y}{x},b=\frac{y^{\prime }}{y}$$

有:
$$tan{\alpha }^{\prime }=\frac{by}{ax}=\frac{b}{a}tan\alpha$$

将上式两边用 $tan\alpha$ 各减和加 即:
$$tan\alpha -tan{\alpha }^{\prime }=tan\alpha -\frac{b}{a}tan\alpha =tan\alpha (1-\frac{b}{a})$$

$$tan\alpha +tan{\alpha }^{\prime }=tan\alpha +\frac{b}{a}tan\alpha =tan\alpha (1+\frac{b}{a})$$

因为:
$$\begin{array}{rl}tana+tanb& =\frac{sina}{cosa}+\frac{sinb}{cosb}\\ & =\frac{sinacosb+sinbcosa}{cosacosb}\\ & =\frac{sin(a+b)}{cosacosb}\end{array}$$

所以:
$$\frac{sin(\alpha -{\alpha }^{\prime })}{cos\alpha cos{\alpha }^{\prime }}=\frac{a-b}{a}tan\alpha$$

$$\frac{sin(\alpha +{\alpha }^{\prime })}{cos\alpha cos{\alpha }^{\prime }}=\frac{a+b}{a}tan\alpha$$

将上面两个式子相除有:
$$\frac{sin(\alpha -{\alpha }^{\prime })}{sin(\alpha +{\alpha }^{\prime })}=\frac{a-b}{a+b}$$

有:
$$sin(\alpha -{\alpha }^{\prime })=\frac{a-b}{a+b}sin(\alpha +{\alpha }^{\prime })$$

那么任意角度变形 $\Delta u$:
$$sin(\frac{\Delta u}{2})=\frac{a-b}{a+b}sin(\alpha +{\alpha }^{\prime })$$

那么最大度变形 $\omega$:
$$sin(\frac{\omega }{2})=\frac{a-b}{a+b}$$

等角变换
如果是等角变换,那么 $\Delta u=\omega =0$, 那么 $a=b$。

4) 变形椭圆
上面三种变形都可以使用变形椭圆来刻画。

在球面上取一个微分圆,投影到球面上会变成一个椭圆。这种方法叫变形椭圆。

图片出处-新编地图学教程第二章

$m$经线长度比, $n$纬线长度比。
$$\frac{X^{\prime }}{X}=m\frac{Y^{\prime }}{Y}=n$$

带入到圆公式$x^2+y^2=1$, 有:
$$\frac{X^{\prime 2}}{m^2}+\frac{Y^{\prime 2}}{n^2}=1$$

因此说明, 地球面上的微小圆,投影后通常会变为椭圆。

3、圆柱投影

当圆柱的中心轴与地球自转轴重合时, 称为正圆柱投影。
当圆柱的中心轴与地球自转轴垂直时, 横为正圆柱投影。

正圆柱投影特点:

• 纬线是一组彼此平行的直线。
• 经线是一组垂直于纬线的直线，且经线间隔相等

4、墨卡托投影

等角正轴圆柱投影。由荷兰地图学家墨卡托（Mercator Gerardus,1512—1594）于1569年所创设，故又名墨卡托投影。

推导方式1

参考

其中 $R$ 是地球半径, 经度 $\lambda$,纬度 $\varphi$:
$$\varphi \in (-\frac{\pi }{2},\frac{\pi }{2})$$

$$\lambda \in (-\pi ,\pi )$$

B、C所在纬线圈的半径:
$$r=Rcos\varphi$$

BC的弧长为纬线圈半径与两点经度差之积:
$$BC=r\Delta \lambda =Rcos\varphi \Delta \lambda$$

$$AB=R\Delta \varphi$$

投影到平面后:
$$\begin{gathered} B^{\prime }{C}^{\prime }=\Delta x \\ {A}^{\prime }{B}^{\prime }=\Delta y \end{gathered}$$

因为投影后将每一个纬线圈都放大到与赤道圆相同大小，所以投影后$\Delta x$长度就是A’D’经度夹角与赤道圆半径的乘积，即：
$$\Delta x=R\Delta \lambda$$

由于投影后需要保证航线角相同，所以:
$$\frac{BC}{AB}=\frac{B^{\prime }{C}^{\prime }}{A^{\prime }{B}^{\prime }}$$

带人有:
$$\frac{Rcos\varphi \Delta \lambda }{R\Delta \varphi }=\frac{\Delta x}{\Delta y}$$

$$\Rightarrow \frac{\Delta y}{\Delta \varphi }=\frac{\Delta x}{\Delta \lambda \cos \varphi }$$

$$\Rightarrow \frac{\Delta y}{\Delta \varphi }=\frac{R\Delta \lambda }{\Delta \lambda \cos \varphi }=\frac{R}{cos\varphi }$$

根据导数定义，上式即:
$$y^{\prime }(\varphi )=\frac{R}{\cos \varphi }$$

下面积分求$y(\varphi )$就可以了:
$$\begin{array}{rl}y(\varphi )& =\int y^{\prime }(\varphi )d\varphi =R\int \frac{1}{\cos \varphi }d\varphi \\ & =R\int \frac{1}{{\cos }^2\varphi }d\sin \varphi =R\int \frac{1}{1-{\sin }^2\varphi }d\sin \varphi \end{array}$$

设$t=\sin \varphi$:
$$y(\varphi )=R\int \frac{1}{1-t^2}dt=\frac{R}{2}\int (\frac{1}{1+t}+\frac{1}{1-t})dt$$

易得:
$$y(\varphi )=\frac{R}{2}\ln |\frac{1+t}{1-t}|=\frac{R}{2}\ln |\frac{1+\sin \varphi }{1-\sin \varphi }|$$

$$y(\varphi )=\frac{R}{2}\ln |\frac{(1+\sin \varphi {)}^2}{1-{\sin }^2\varphi }|=R\ln \frac{1+\sin \varphi }{\cos \varphi }$$

推导方式2

参考1

参考2
纬度使用 $\theta $ 表示。

$$\begin{array}{rl}x& =\lambda \\ y& =f(\varphi )\end{array}$$

投影后的 $y$ 坐标是关于纬度 $\varphi$ 的函数。

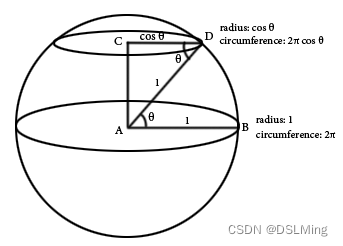
赤道的周长:
$$2\pi R$$

D点所在纬度圆的周长:
$$2\pi R\cos \theta$$

因为所有纬度投影后都与赤道长度相同, 所以纬度处的任何线 $\theta$ 最终都会水平拉伸$1/\cos \theta$

最后，为了满足等角的性质, 地图中水平拉伸某个因子的任何部分，例如 $k$ ，必须由相同的因子 $k $垂直拉伸。这样做可以保留地图该部分的角度：

因此, 水平方向(x)被拉伸了$1/\cos \theta$, 那么垂直方向(x)也会被拉伸 $1/\cos \theta$。

但是 $kx$ 和 $ky$ 这种线性等比缩放只有在这个面积非常小的情况小才成立。用极限表示就是:
$$li{m}_{\Delta \theta \to 0}\frac{\Delta y}{\Delta \theta }=\frac{dy}{d\theta }=\frac{1}{cos\theta }$$

实现代码

//方法一
  //[114.32894, 30.585748]
function latLng2WebMercator(lng, lat) {
    var earthRad = 6378137.0;
    var x = lng * Math.PI / 180 * earthRad;
    var a = lat * Math.PI / 180;
    var y = earthRad / 2 * Math.log((1.0 + Math.sin(a)) / (1.0 - Math.sin(a)));

    //[12727039.383734727, 3579066.6894065146]
    return [x, y];
}

//方法二
function latLng2WebMercator2 (lng, lat)
{
    var x = lng *20037508.34/180;
    var y = Math.log(Math.tan((90+lat)*Math.PI/360))/(Math.PI/180);
    y = y *20037508.34/180;
    return [x, y];
}