2D Convex Collision Detection Algorithm

落羽归尘

已于 2023-08-18 17:56:09 修改

阅读量1.2k

点赞数 1

文章标签：其他

于 2021-11-10 18:04:33 首次发布

本文链接：https://blog.csdn.net/qq_21933647/article/details/121246880

版权

1. Separating Axis Theorem (SAT)

2. Gilbert Johnson Keerthi (GJK)

2.5 自行迭代求取方向 2D Convex GJK：

1. Separating Axis Theorem (SAT)

1. 1 凸多边形

如果一个多边形内部任意两点（包含顶点）间的线段位于多边形的内部或边上，那这种多边形是凸多边形。

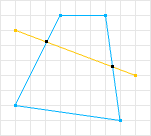
非凸多边形的实例：

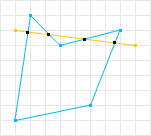
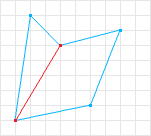
通常一个非凸多边形可以划分为两个以上的凸多边形：

1.2 投影（Projection）

一般地，用光线照射物体，在某个平面（地面、墙壁等）上得到的影子叫做物体的投影。

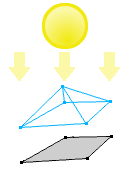
通常一个立体的在某一个平面的投影为一个多边形。而在这里，我们主要关注2D的碰撞检测，所以接下来我们需要清楚在多边形在直线上的投影，下图中右下方独立的蓝色和粉红色线段即为多边形在直线（灰色虚线）上的投影。

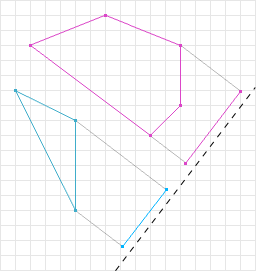
多边形在轴上投影的伪代码如下所示：

function Projection(Convex shape, Axis axis){
  double min = axis.dot(shape.vertices[0]);
  double max = min;
  for (int i = 1; i < shape.vertices.length; i++) {
    // NOTE: the axis must be normalized to get accurate projections
    double p = axis.dot(shape.vertices[i]);
    if (p < min) {
       min = p;
    } else if (p > max) {
       max = p;
    }
  }
  Projection proj = new Projection(min, max);
  return proj;
}

1.3 分离轴定理

若两个凸多边形没有发生碰撞，则总会存在一条直线，两个多边形在这条直线上的投影没有重叠，如图6右侧图所示，蓝色线段和粉红色线段没有重叠部分，其中右侧图中灰色线就是一条分离轴（主观理解是下图左侧图的虚线应该叫分离轴，但是这是错误的）。

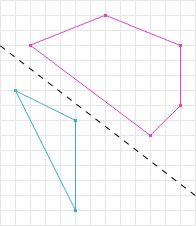
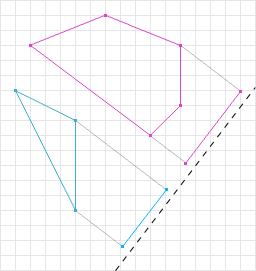
若两个多边形碰撞，则无法找到这样一条分离轴，能使两个多边形在直线上的投影不重叠，这种情况的实例如图7所示，两个多边形在任何一条轴上的投影都有重叠部分。

通常情况下，SAT需要测试很多条轴（下文将解释如何获取这些轴axes），但是只要可以找到一条轴，使多边形投影不重叠，即可判断两多边形不碰撞，SAT算法伪代码如下，true 为碰撞，false为不碰撞：

function SAT(Convex shape1,Convex shape2,Axis[] axises){
// loop over the axes
for (int i = 0; i < axises.length; i++) {
  Axis axis = axises[i];
  // project both shapes onto the axis
  Projection p1 = shape1.project(axis);
  Projection p2 = shape2.project(axis);
  // do the projections overlap?
  if (!p1.overlap(p2)) {
    // then we can guarantee that the shapes do not overlap
    return false;
  }
}
return true;
}

1.4 分离轴获取

这个部分我们将如何获取分离轴，即上方伪代码中的Axis[] axises 的获取方式。SAT算法作者提出了一个非常棒的想法：选取多边形每条边的垂线。

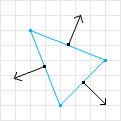
对于一个多边而言，根据其各条边，可以确定的分离轴伪代码如下：

function GetAxises(Convex shape){
  Vector[] axes = new Vector[shape.vertices.length];
  // loop over the vertices
  for (int i = 0; i < shape.vertices.length; i++) {
    // get the current vertex
    Vector p1 = shape.vertices[i];
    // get the next vertex
    Vector p2 = shape.vertices[i + 1 == shape.vertices.length ? 0 : i + 1];
    // subtract the two to get the edge vector
    Vector edge = p1.subtract(p2);
    // get either perpendicular vector
    Vector normal = edge.perp();
    // the perp method is just (x, y) =&gt; (-y, x) or (y, -x)
    axes[i] = normal;
  }
}

获取分离轴、再根据分离轴确认两多边形是否碰撞的流程如下：

function SATCollisionDetection(Convex shape1, Convex shape2){

   Axis[] axes1 = shape1.GetAxises();
   Axis[] axes2 = shape2.GetAxises();
   // loop over the axes1
   for (int i = 0; i < axes1.length; i++) {
     Axis axis = axes1[i];
     // project both shapes onto the axis
     Projection p1 = shape1.Projection(axis);
     Projection p2 = shape2.Projection(axis);
     // do the projections overlap?
     if (!p1.overlap(p2)) {
       // then we can guarantee that the shapes do not overlap
       return false;
     }
   }
   // loop over the axes2
   for (int i = 0; i < axes2.length; i++) {
     Axis axis = axes2[i];
     // project both shapes onto the axis
     Projection p1 = shape1.Projection(axis);
     Projection p2 = shape2.Projection(axis);
     // do the projections overlap?
     if (!p1.overlap(p2)) {
       // then we can guarantee that the shapes do not overlap
       return false;
     }
   }
   // if we get here then we know that every axis had overlap on it
   // so we can guarantee an intersection
   return true;
}

2. Gilbert Johnson Keerthi (GJK)

2.1 Minkowski sum 介绍

给定向量集合 A、B，定义他们的Minkowski sum为：

$A + B = \{\vec{a} + \vec{b} \: \mid \: \vec{a} \in A, \vec{b} \in B\}$

定义向量集合 A、B的Minkowski Difference 为：

$A - B = \{\vec{a} - \vec{b} \: \mid \: \vec{a} \in A, \vec{b} \in B\}$

2.2 GJK 算法核心思想

本质就是利用Minkowski差来判断2个几何体有没碰撞。因为如果碰撞了，那么2个几何体至少包含了同一个点，也就意味着它们的Minkowski差（第二幅图）必然包含原点：

2.3 单纯形 Simplex

通常情况下，我们使用GJK 算法核心思想去判断两个凸多边形是否碰撞，不会直接去求两个多边形的Minkowski差。GJK算法告诉我们需要在Minkowski差多边形内构建单纯形，然后判断单纯形是否包含原点，如果包含原点，则发生碰撞。接下来，我们将介绍什么是单纯形，以及如何“在Minkowski差多边形内”构建单纯形（见2.4）。

单纯形或者n-单纯形是和三角形类似的n维几何体。精确的讲，单纯形是某个n维以上的欧几里得空间中的（n+1）个仿射无关（也就是没有m-1维平面包含m+1个点；这样的点集被称为处于一般位置）的点的集合的凸包。

示例：

0 阶单纯形：

1 阶单纯形：

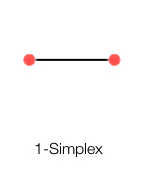
2阶单纯形：

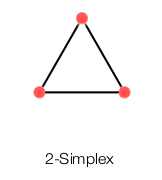
3阶单纯形：

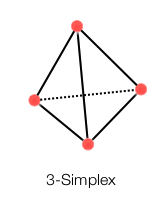
2.4 Support Function

接下来阐述一下怎么构建单纯形，单纯形的构建过程为迭代过程，每一步都会调用support function （公用叫法）。support function 返回值为Minkowski差多边形内的一个点。

support function ：

假设初始方向为 $\vec{a}$ ，任选其中一个多边形的所有顶点投影到这个方向上，求出最大点。
再将初始方向取反，即 $-\vec{a}$ 。然后将另外一个多边形的所有顶点投影到这个方向上，求出最大点。
获得的两个点相减，即可得到单纯形上的一点。

Point support(Convex shape1, Convex shape2, Vector a) {
  // d is a vector direction (doesn't have to be normalized)
  // get points on the edge of the shapes in opposite directions
  Point p1 = shape1.getFarthestPointInDirection(d);
  Point p2 = shape2.getFarthestPointInDirection(d.negative());
  // perform the Minkowski Difference
  Point p3 = p1.subtract(p2);
  // p3 is now a point in Minkowski space on the edge of the Minkowski Difference
  return p3;
}

举个栗子：

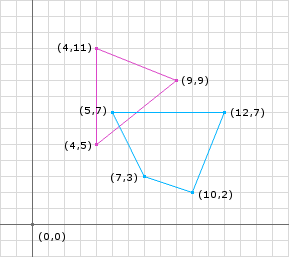
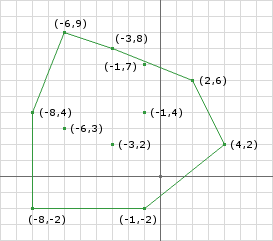
创建单纯形：

iteration 1: 取 $\vec{a}=(1,0)$ ，粉色多边形在 $\vec{a}$ 上投影最远的点为 $p_{1}(9,9),$ 蓝色多边形在- $\vec{a}$ 上投影的最大点为 $p_{2}(5,7)$ ，他们的差值为 $p_{3}(4,2)$

p1 = (9, 9)
p2 = (5, 7)
p3 = p1 - p2 = (4, 2)

iteration 2: 取 $\vec{a}=(-1,0)$ ，粉色多边形在 $\vec{a}$ 上投影最远的点为 $p_{1}(4,5)$ 蓝色多边形在- $\vec{a}$ 上投影的最大点为 $p_{2}(12,7)$ ，他们的差值为 $p_{3}(-8,-2)$

p1 = (4, 5)
p2 = (12, 7)
p3 = p1 - p2 = (-8, -2)

iteration 3：取 $\vec{a}=(0,1)$ ，粉色多边形在 $\vec{a}$ 上投影最远的点为 $p_{1}(4,11)$ 蓝色多边形在- $\vec{a}$ 上投影的最大点为 $p_{2}(10,2)$ ，他们的差值为 $p_{3}(-6,9)$

p1 = (4, 11)
p2 = (10, 2)
p3 = p1 - p2 = (-6, 9)

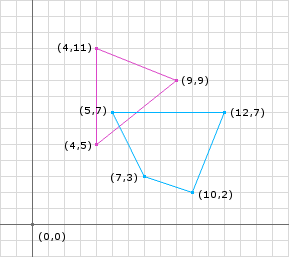
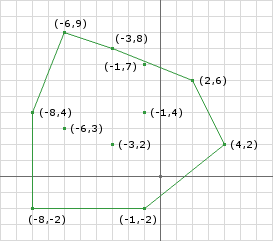
至此我们获得的单纯形为如图所示：

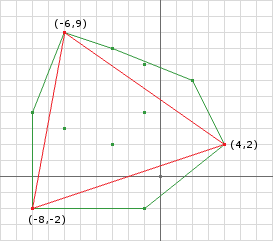
此刻构建的单纯形，并不包含原点，但是我们如果对iteration3 中的 $\vec{a}$ 重新选取，选取 $\vec{a}=(0,-1)$ ,则有：

p1 = (4, 5)
p2 = (5, 7)
p3 = p1 - p2 = (-1, -2)

重新选取 $\vec{a}$ 之后的单纯形为：

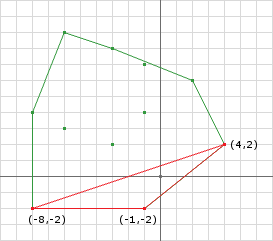
事实证明方向 $\vec{a}$ 的选择会影响结果。那我们如何更好地选取 $\vec{a}$ 呢，或者如何改进迭代算法呢？

2.5 自行迭代求取方向 2D Convex GJK：

迭代方向的求取如下伪代码第六行：

d = ...   /// initial direction
a = support(..., d)   /// first point 
b = support(..., -d)  /// second point
AB = b - a
AO = ORIGIN - a
d = (AB x AO) x AB  /// new direction ！！！！！
c = support(..., d)  /// final point for 2D simplex

那么引入迭代方向之后的GJK思路为：

1. 判断当前构建的单纯形是否包含原点；

2. 我们是否能逼近原点.（迭代构建新单纯形的过程中尽量保留上一步中离原点近的边）

退出条件：

1. 单纯形包含原点；

2. 新的support点与迭代方向的点乘结果小于0；

具体的伪代码如下所示：

Vector d = // choose a search direction
// get the first Minkowski Difference point
Simplex.add(support(A, B, d));
// negate d for the next point
d.negate();
// start looping
while (true) {
  // add a new point to the simplex because we haven't terminated yet
  Simplex.add(support(A, B, d));
  // make sure that the last point we added actually passed the origin
  if (Simplex.getLast().dot(d) <= 0) {
    // if the point added last was not past the origin in the direction of d
    // then the Minkowski Sum cannot possibly contain the origin since
    // the last point added is on the edge of the Minkowski Difference
    return false;
  } else {
    // otherwise we need to determine if the origin is in
    // the current simplex
    if (containsOrigin(Simplex, d) {
      // if it does then we know there is a collision
      return true;
    }
  }
}

boolean containsOrigin(Simplex s, Vector d) {
  // get the last point added to the simplex
  a = Simplex.getLast();
  // compute AO (same thing as -A)
  ao = a.negate();
  if (Simplex.points.size() == 3) {
    // then its the triangle case
    // get b and c
    b = Simplex.getB();
    c = Simplex.getC();
    // compute the edges
    ab = b - a;
    ac = c - a;
    // compute the normals
    abPerp = tripleProduct(ac, ab, ab);
    acPerp = tripleProduct(ab, ac, ac);
    // is the origin in R4
    if (abPerp.dot(ao) > 0) {
      // remove point c
      Simplex.remove(c);
      // set the new direction to abPerp
      d.set(abPerp);
    } else {
      // is the origin in R3
      if (acPerp.dot(ao) > 0) {
        // remove point b
        Simplex.remove(b);
        // set the new direction to acPerp
        d.set(acPerp);
      } else{
        // otherwise we know its in R5 so we can return true
        return true;
      }
    }
  } else {
    // then its the line segment case
    b = Simplex.getB();
    // compute AB
    ab = b - a;
    // get the perp to AB in the direction of the origin
    abPerp = tripleProduct(ab, ao, ab);
    // set the direction to abPerp
    d.set(abPerp);
  }
  return false;
}

咱接着这个图结合上述伪代码继续唠：

outside of loop：

d = (1, -1);
p1 = support(A, B, d) = (9, 9) - (5, 7) = (4, 2);
Simplex.add(p1);
d.negate() = (-1, 1);

loop：

iteration1：

last = support(A, B, d) = (4, 11) - (10, 2) = (-6, 9);
proj = (-6, 9).dot(-1, 1) = 6 + 9 = 15
// we past the origin so check if we contain the origin
// we dont because we are line
// get the new direction by (AB x AO) x AB 
AB = (-6, 9) - (4, 2)  = (-10, 7);
AO = (0, 0) - (-6, 9) = (6, -9);
(AB x AO) x AB = AO(149) - AB(-123) 
               = (894, -1341) - (1230, -861) 
               = (-336, -480)
               = (-0.573, -0.819)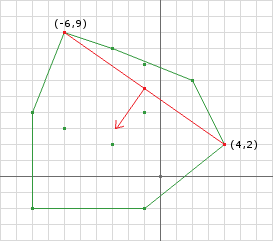

iteration2：

last = support(A, B, d) = (4, 5) - (12, 7) = (-8, -2)
proj = (-8, -2).dot(-336, -480) = 2688 + 960 = 3648
// we past the origin so check if we contain the origin
// the new direction will be the perp of (4, 2) and (-8, -2)
// and the point (-6, 9) can be removed
AB = (-8, -2) - (4, 2)  = (-12, -4);
AO = (0, 0) - (-8, -2) = (8, 2);
(AB x AO) x AB = AO(160) - AB(-104) 
               = (1280, 320) - (1248, 416) 
               = (32, -96)
               = (0.316, -0.948)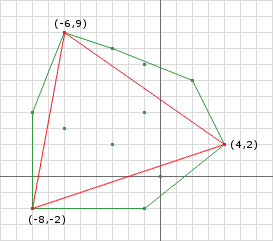

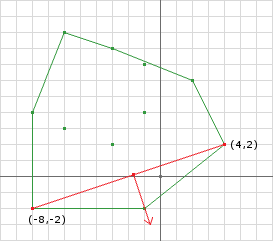
注解：在第二次循环之后，发现原点不在单纯形内。此时我们将单纯形中的点（-6,9）移除，继续迭代

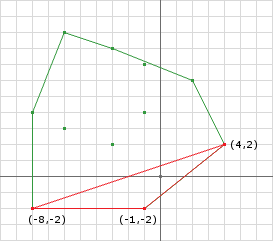
iteration3：

last = support(A, B, d) = (4, 5) - (5, 7) = (-1, -2)
proj = (-1, -2).dot(32, -96) = -32 + 192 = 160
// we past the origin so check if we contain the origin

落羽归尘

关注

1
点赞
踩
9

收藏

觉得还不错? 一键收藏
1
评论
2D Convex Collision Detection Algorithm

1. Separating Axis Theorem (SAT) 1. 1 凸多边形如果一个多边形内部任意两点（包含顶点）间的线段位于多边形的内部或边上，那这种多边形是凸多边形。图1 非凸多边形的实例：图2 通常一个非凸多边形可以划分为两个以上的凸多边形：图31.2 投影（Projection）一般地，用光线照射物体，在某个平面（地面、墙壁等）上得到的影子叫做物体的投影。图4...
复制链接

扫一扫