【Python】深度学习基础知识——梯度下降详解和示例

尽管梯度下降（gradient descent）很少直接用于深度学习，但它是随机梯度下降算法的基础，也是很多问题的来源，如由于学习率过大，优化问题可能会发散，这种现象早已在梯度下降中出现。本文通过原理和示例对一维梯度下降和多元梯度下降进行详细讲解，以帮助大家理解和使用。

一维梯度下降

理论

从公式推导变化中，可以看出，目标函数确定之后，便是一直迭代展开，如果导数不为0则继续展开，直到满足停止条件。也可以帮助理解为什么要防止梯度为0的现象出现。
此外，也可以看到初始值和步长也影响最后的结果，在深度学习中就是我们设置的初始权重和学习率。

示例

下面我们来展示如何实现梯度下降。为了简单起见，我们选用目标函数f(x)=x**2。 尽管我们知道x=0时，目标函数取得最小值。但我们仍然使用这个简单的函数来观察
x的变化。

import torch
import numpy as np
def f(x):  # 目标函数
    return x ** 2

def f_grad(x):  # 目标函数的梯度(导数)
    return 2 * x

def gd(eta, f_grad):
    x = 20.0
    results = [x]
    for i in range(20):
        x -= eta * f_grad(x)
        results.append(float(x))
    print(f'epoch 20, x: {x:f}')
    return results

results = gd(0.2, f_grad)

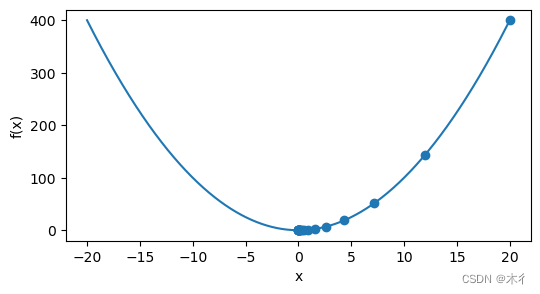
在示例中，我们使用x=20作为初始值，设置步长为0.2,。使用梯度下降法迭代x=20次。得到结果为：

epoch 20, x: 0.000731

可以看到，结果0.000731很接近真实结果0。

对于x的优化过程进行可视化，如下图所示。

import matplotlib.pyplot as plt

def show_trace(results, f):
    n = max(abs(min(results)), abs(max(results)))
    f_line = torch.arange(-n, n, 0.01)
    
    # 设置图形大小
    plt.figure(figsize=(6, 3))
    
    # 绘制 f_line 的函数图像
    plt.plot(f_line.numpy(), [f(x) for x in f_line.numpy()], '-')
    
    # 绘制 results 的散点图
    plt.scatter(results, [f(x)  for x in results], marker='o')
    
    # 设置 x 轴和 y 轴的标签
    plt.xlabel('x')
    plt.ylabel('f(x)')
    
    # 显示图形
    plt.show()


show_trace(results, f)

学习率

学习率的大小对结果的影响也很大，如果设置过小，很慢才能到达最优解，如果设置过大，可能会跳过最优解。

设置过小示例

当设置为0.02时。

def f(x):  # 目标函数
    return x ** 2

def f_grad(x):  # 目标函数的梯度(导数)
    return 2 * x

def gd(eta, f_grad):
    x = 20.0
    results = [x]
    for i in range(20):
        x -= eta * f_grad(x)
        results.append(float(x))
    print(f'epoch 20, x: {x:f}')
    return results

results = gd(0.02, f_grad)

epoch 20, x: 8.840049

可以看出，经过20次迭代，值为 8.840049，与我们可知的真实值0相差很远。
过程可视化：

import matplotlib.pyplot as plt

def show_trace(results, f):
    n = max(abs(min(results)), abs(max(results)))
    f_line = torch.arange(-n, n, 0.01)
    
    # 设置图形大小
    plt.figure(figsize=(6, 3))
    
    # 绘制 f_line 的函数图像
    plt.plot(f_line.numpy(), [f(x) for x in f_line.numpy()], '-')
    
    # 绘制 results 的散点图
    plt.scatter(results, [f(x)  for x in results], marker='o')
    
    # 设置 x 轴和 y 轴的标签
    plt.xlabel('x')
    plt.ylabel('f(x)')
    
    # 显示图形
    plt.show()


show_trace(results, f)

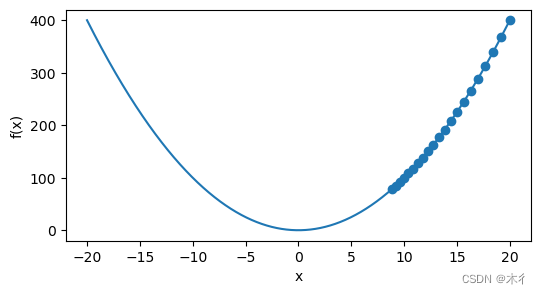
距离最小值点还有较大距离。

设置过大示例

当设置为0.9时：

def f(x):  # 目标函数
    return x ** 2

def f_grad(x):  # 目标函数的梯度(导数)
    return 2 * x

def gd(eta, f_grad):
    x = 20.0
    results = [x]
    for i in range(20):
        x -= eta * f_grad(x)
        results.append(float(x))
    print(f'epoch 20, x: {x:f}')
    return results

results = gd(0.9, f_grad)

输出结果：

epoch 20, x: 0.230584

经过20轮迭代，数值为0.230584，与我们可知的0也有一定差距，现在不确定是过拟合还是欠拟合，通过迭代过程可视化，可以看到优化过程为：

可知，在某一次迭代时已经达到最优，但没有停止，在迭代20次时，过拟合了，偏离了最优解。

局部最小值

为了演示非凸函数的梯度下降，考虑函数f(x)=x*cos(cx),其中c为常数。 这个函数有无穷多个局部最小值。 根据我们选择的学习率，我们最终可能只会得到许多解的一个。 下面的例子说明了（不切实际的）高学习率如何导致较差的局部最小值。

c = torch.tensor(0.15 * np.pi)

def f(x):  # 目标函数
    return x * torch.cos(c * x)

def f_grad(x):  # 目标函数的梯度
    return torch.cos(c * x) - c * x * torch.sin(c * x)



def show_trace(results, f):
    n = max(abs(min(results)), abs(max(results)))
    f_line = torch.arange(-n, n, 0.01)
    
    # 设置图形大小
    plt.figure(figsize=(6, 3))
    
    # 绘制 f_line 的函数图像
    plt.plot(f_line.numpy(), [f(x) for x in f_line.numpy()], '-')
    
    # 绘制 results 的散点图
    plt.scatter(results, [f(x)  for x in results], marker='o')
    
    # 设置 x 轴和 y 轴的标签
    plt.xlabel('x')
    plt.ylabel('f(x)')
    
    # 显示图形
    plt.show()
    
def gd(eta, f_grad):
    x = 20.0
    results = [x]
    for i in range(20):
        x -= eta * f_grad(x)
        results.append(float(x))
        print(f'epoch i: {i:f}, x: {x:f}')
    return results

show_trace(gd(2, f_grad), f)

输出：

epoch i: 0.000000, x: 22.000000
epoch i: 1.000000, x: 6.400991
epoch i: 2.000000, x: 9.138650
epoch i: 3.000000, x: 2.015201
epoch i: 4.000000, x: 2.395759
epoch i: 5.000000, x: 3.581714
epoch i: 6.000000, x: 7.167863
epoch i: 7.000000, x: 7.531582
epoch i: 8.000000, x: 6.554027
epoch i: 9.000000, x: 8.878934
epoch i: 10.000000, x: 2.659682
epoch i: 11.000000, x: 4.416834
epoch i: 12.000000, x: 9.026052
epoch i: 13.000000, x: 2.285584
epoch i: 14.000000, x: 3.234577
epoch i: 15.000000, x: 6.186752
epoch i: 16.000000, x: 9.443290
epoch i: 17.000000, x: 1.366405
epoch i: 18.000000, x: 0.539987
epoch i: 19.000000, x: -1.267501

可知，迭代过程中，经过了多个局部最小点，最后也错过了全局最小点。

多元梯度下降

理论

示例

import torch
import matplotlib.pyplot as plt
def train_2d(trainer, steps=20, f_grad=None):  #@save
    """用定制的训练机优化2D目标函数"""
    # s1和s2是稍后将使用的内部状态变量
    x1, x2, s1, s2 = -5, -2, 0, 0
    results = [(x1, x2)]
    for i in range(steps):
        if f_grad:
            x1, x2, s1, s2 = trainer(x1, x2, s1, s2, f_grad)
        else:
            x1, x2, s1, s2 = trainer(x1, x2, s1, s2)
        results.append((x1, x2))
    print(f'epoch {i + 1}, x1: {float(x1):f}, x2: {float(x2):f}')
    return results

def show_trace_2d(f, results):  #@save
    """显示优化过程中2D变量的轨迹"""
    plt.figure(figsize=(6, 3))
    plt.plot(*zip(*results), '-o', color='#ff7f0e')
    x1, x2 = torch.meshgrid(torch.arange(-5.5, 1.0, 0.1),
                          torch.arange(-3.0, 1.0, 0.1), indexing='ij')
    plt.contour(x1, x2, f(x1, x2), colors='#1f77b4')
    plt.xlabel('x1')
    plt.ylabel('x2')

def f_2d(x1, x2):  # 目标函数
    return x1 ** 2 + 2 * x2 ** 2

def f_2d_grad(x1, x2):  # 目标函数的梯度
    return (2 * x1, 4 * x2)

def gd_2d(x1, x2, s1, s2, f_grad):
    g1, g2 = f_grad(x1, x2)
    return (x1 - eta * g1, x2 - eta * g2, 0, 0)

eta = 0.1
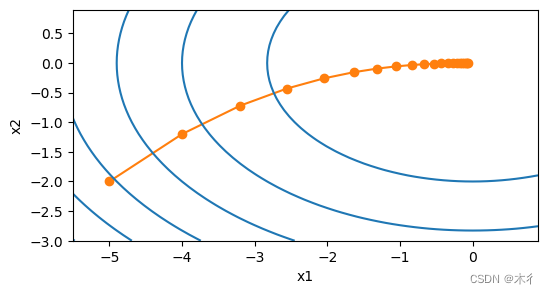
show_trace_2d(f_2d, train_2d(gd_2d, f_grad=f_2d_grad))

在示例中，我们将学习率设置为0.1，优化变量x的轨迹如下图所示。值接近其位于[0,0]的最小值。 虽然进展相当顺利，但相当缓慢。初始值为[-2,-5]

总结

如何更好更高效的选择学习率，是一件重要的事情，如果我们把它选得太小，就没有什么进展；如果太大，得到的解就会振荡，甚至可能发散。
同时，初始值的选择也会影响最终的结果。