(十) 图

1、定义：由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为：G(V,E)，G表示一个图，V是图G中顶点的集合，E是图G中边的集合。线性表中数据元素叫元素，树中叫结点，在图中数据元素叫顶点。线性表可以没有数据元素称为空表，树中可以没有结点叫空树，图结构强调顶点集合V要有穷非空。线性表中，相邻的数据元素之间具有线性关系，树结构中，相邻两层的结点具有层次关系，图结构中，任意两个顶点之间都可能有关系，顶点之间的逻辑关系用边来表示，边集可以是空的。

2、无向图：若顶点Vi到Vj之间的边没有方向，则称该边为无向边，用无序偶（Vi，Vj）来表示。顶点V1和V2互为邻接点。顶点V的度是和V相关联边的数目，记为TD(V)，顶点A与顶点B互为邻接点，边（A,B）依附于顶点A与B上，顶点A的度为3。

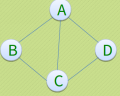
G1是一个无向图，G1={V1，E1}
V1={A,B,C,D}
E1={(A,B),(B,C),(C,D),(D,A),(A,C)}

3、有向图：若从顶点Vi到Vj的边有方向，则称该边有向边或弧。用有序偶<Vi,Vj>来表示，Vi称为弧尾，Vj称为弧头，顶点V1邻接到顶点V2,顶点V2邻接自顶点V1。以顶点V为头弧数目称为V的入度，记为ID（V），以V为尾弧的数目称为V出度，记为OD（V），因此顶点V的度为TD（V）=ID（V）+OD（V）。A入度2,出度1,A的度是3。

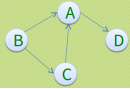
G2是一个有向图，G2={V2，E2}
V2={A，B，C，D}
E2={<B,A>,<B,C>,<C,A>,<A,D>}

4、稀疏图和稠密图：通常认为边或弧数小于n*logn（n是顶点的个数）的图称为稀疏图，反之称为稠密图。有些图的边或弧带有与它相关的数字，这种与图的边或弧相关的数叫做权，带权的图通常称为网。

5、连通图：在无向图G中，如果从顶点V1到顶点V2有路径，则称V1和V2是连通的，如果对于图中任意两个顶点Vi和Vj都是连通的，则称G是连通图。在有向图G中，如果对于每一对Vi到Vj都存在路径，则称G是强连通图。

6、邻接矩阵：对于无向图来说，用两个数组来表示图，一个一维数组存储图中顶点信息，一个二维数组（称为邻接矩阵）存储图中的边或弧的信息。判定任意两顶点是否有边无边;要知道某个顶点的度，其实就是这个顶点Vi在邻接矩阵中第i行（或第i列）的元素之和;求顶点Vi的所有邻接点就是将矩阵中第i行元素扫描一遍，arc[i][j]为1就是邻接点。

#define MAXVEX 100      // 最大顶点数
#define INFINITY 65535  // 用65535来代表无穷大
typedef struct {
  char vexs[MAXVEX];          // 顶点表
  int arc[MAXVEX][MAXVEX];    // 邻接矩阵
  int numVertexes, numEdges;  // 图中当前的顶点数和边数
} MGraph;

// 建立无向网图的邻接矩阵
void CreateMGraph(MGraph* G) {
  int i, j, k, w;
  printf("请输入顶点数和边数：\n");
  scanf("%d %d", &G->numVertexes, &G->numEdges);
  for (i = 0; i < G->numVertexes; i++) scanf("%c", &G->vexs[i]);
  for (i = 0; i < G->numVertexes; i++)
    for (j = 0; j < G->numVertexes; j++)
      G->arc[i][j] = INFINITY;  // 邻接矩阵初始化
  for (k = 0; k < G->numEdges; k++) {
    printf("请输入边(Vi,Vj)上的下标i,下标j和对应的权w:\n");
    scanf("%d %d %d", &i, &j, &w);
    G->arc[i][j] = w;
    G->arc[j][i] = G->arc[i][j];  // 是无向网图，对称矩阵
  }
}

7、邻接表：图中顶点用一个一维数组存储，图中每个顶点Vi的所有邻接点构成一个线性表，由于邻接点的个数不确定，选择用单链表来存储。

#define MAXVEX 100
typedef struct EdgeNode			// 边表结点
{
         int adjvex;					// 邻接点域，存储该顶点对应的下标
         int weight;					// 用于存储权值，对于非网图可以不需要
         struct EdgeNode *next;		// 链域，指向下一个邻接点
} EdgeNode;

typedef struct VertexNode		// 顶点表结点
{
         char data;					// 顶点域，存储顶点信息
          EdgeNode *firstEdge;		// 边表头指针
} VertexNode, AdjList[MAXVEX];

typedef struct
{
         AdjList adjList;
         int numVertexes, numEdges;	// 图中当前顶点数和边数
} GraphAdjList;

// 建立图的邻接表结构
void CreateALGraph(GraphAdjList *G)
{
	int i, j, k;
	EdgeNode *e;
	printf("请输入顶点数和边数：\n");
	scanf("%d %d", &G->numVertexes, &G->numEdges);
	
	// 读取顶点信息，建立顶点表
	for( i=0; i < G->numVertexes; i++ )
	{
	         scanf("%c", &G->adjList[i].data);
	         G->adjList[i].firstEdge = NULL;		// 初始化置为空表
	}
	for( k=0; k < G->numEdges; k++ )
	{
		printf("请输入边(Vi,Vj)上的顶点序号：\n");
		scanf("%d %d", &i, &j);
		
		e = (EdgeNode *)malloc(sizeof(EdgeNode));
		e->adjvex = j;						// 邻接序号为j
		e->next = G->adjList[i].firstEdge;
		G->adjList[i].firstEdge = e;
		
		e = (EdgeNode *)malloc(sizeof(EdgeNode));
		e->adjvex = i;						// 邻接序号为i
		e->next = G->adjList[j].firstEdge;
		G->adjList[j].firstEdge = e;
	}
}

8、邻接表（网）：对于带权值的网图，可以在边表结点定义中再增加一个数据域来存储权值即可

 9、边集数组：两个一维数组构成，一个是存储顶点的信息，另一个是存储边的信息，这个边数组每个数据元素由一条边的起点下标、终点下标和权组成。

 10、深度优先遍历：DFS，先彻底查找完一个房间再开始另一个房间的搜索。

#define TRUE 1
#define FALSE 0
#define MAX 256
typedef int Boolean;  // 这里我们定义Boolean为布尔类型，其值为TRUE或FALSE
Boolean visited[MAX];  // 访问标志的数组
void DFS(MGraph G, int i) {
  int j;
  visited[j] = TRUE;         // 访问过的顶点设置为TRUE
  printf("%c ", G.vexs[i]);  // 打印顶点
  for (j = 0; j < G.numVertexes; j++)
    if (G.arc[i][j] == 1 && !visited[j])
      DFS(G, j);  // 对为访问的邻接顶点递归调用
}

// 邻接矩阵的深度遍历操作
void DFSTraverse(MGraph G) {
  int i;
  for (i = 0; i < G.numVertexes; i++)
    visited[i] = FALSE;  // 初始化所有顶点状态都是未访问过状态
  for (i = 0; i < G.numVertexes; i++)
    if (!visited[i]) DFS(G, i);  // 若是连通图，只会执行一次
}

11、广度优先遍历：BFS，逐步扩大查找范围的方式，利用队列实现

// 邻接矩阵的广度遍历算法
void BFSTraverse(MGraph G)
{
	int i, j;
	Queue Q;
	for( i=0; i < G.numVertexes; i++ ) visited[i] = FALSE;
	initQueue( &Q );
	for( i=0; i < G.numVertexes; i++ )
	{
		if( !visited[i] )
		{
			printf("%c ", G.vex[i]);
			visited[i] = TRUE;
			EnQueue(&Q, i);
			while( !QueueEmpty(Q) )
			{
				DeQueue(&Q, &i);
				for( j=0; j < G.numVertexes; j++ )
				{
					if( G.art[i][j]==1 && !visited[j] )
					{
						printf("%c ", G.vex[j]);
						visited[j] = TRUE;
						EnQueue(&Q, j);
					}
				}
			}
		}
	}
}

12、最小生成树（普里姆算法）

以某顶点为起点，逐步找各个顶点上最小权值的边来构建最小生成树。

// Prim算法生成最小生成树
void MiniSpanTree_Prim(MGraph G)
{
	int min, i, j, k;
	int adjvex[MAXVEX];	// 保存相关顶点下标
	int lowcost[MAXVEX];	// 保存相关顶点间边的权值
	lowcost[0] = 0;			// V0作为最小生成树的根开始遍历，权值为0
	adjvex[0] = 0;			// V0第一个加入
	
	// 初始化操作
	for( i=1; i < G.numVertexes; i++ )
	{
		lowcost[i] = G.arc[0][i];	// 将邻接矩阵第0行所有权值先加入数组
		adjvex[i] = 0;		// 初始化全部先为V0的下标
	}
	
	// 真正构造最小生成树的过程
	for( i=1; i < G.numVertexes; i++ )
	{
		min = INFINITY;		// 初始化最小权值为65535等不可能数值
		j = 1;
		k = 0;
		
		// 遍历全部顶点
		while( j < G.numVertexes )
		{
			// 找出lowcost数组已存储的最小权值
			if( lowcost[j]!=0 && lowcost[j] < min )
			{
				min = lowcost[j];
				k = j;		// 将发现的最小权值的下标存入k，以待使用。
			}
			j++;
		}
		
		// 打印当前顶点边中权值最小的边
		printf("(%d,%d)", adjvex[k], k);
		lowcost[k] = 0;		// 将当前顶点的权值设置为0，表示此顶点已经完成任务，进行下一个顶点的遍历
		
		// 邻接矩阵k行逐个遍历全部顶点
		for( j=1; j < G.numVertexes; j++ )
		{
			if( lowcost[j]!=0 && G.arc[k][j] < lowcost[j] )
			{
				lowcost[j] = G.arc[k][j];
				adjvex[j] = k;	
			}
		}
	}
}

13、最小生成树（克鲁斯卡尔算法）

从边出发，权值在边上，直接去找最小权值的边来构建生成树是自然的想法。

int Find(int* parent, int f) {
  while (parent[f] > 0) f = parent[f];
  return f;
}
// Kruskal算法生成最小生成树
void MiniSpanTree_Kruskal(MGraph G) {
  int i, n, m;
  Edge edges[MAGEDGE];  // 定义边集数组
  int parent[MAXVEX];  // 定义parent数组用来判断边与边是否形成环路
  for (i = 0; i < G.numVertexes; i++) parent[i] = 0;
  for (i = 0; i < G.numEdges; i++) {
    n = Find(parent, edges[i].begin);  // 4 2 0 1 5 3 8 6 6 6 7
    m = Find(parent, edges[i].end);    // 7 8 1 5 8 7 6 6 6 7 7
    if (n != m)  // 如果n==m，则形成环路，不满足！
    {
      parent[n] =
          m;  // 将此边的结尾顶点放入下标为起点的parent数组中，表示此顶点已经在生成树集合中
      printf("(%d, %d) %d ", edges[i].begin, edges[i].end, edges[i].weight);
    }
  }
}

14、最短路径（迪杰斯特拉算法）

网图是两顶点经过的边上权值之和最少的路径。

非网图是两顶点之间经过的边数最少的路径。

#define MAXVEX	9
#define	INFINITY	65535
typedef int    Patharc[MAXVEX];		// 用于存储最短路径下标的数组
typedef int    ShortPathTable[MAXVEX];	// 用于存储到各点最短路径的权值和
void ShortestPath_Dijkstar(MGraph G, int V0, Patharc *P, ShortPathTable *D)
{
	int v, w, k, min;
	int final[MAXVEX];		// final[w] = 1 表示已经求得顶点V0到Vw的最短路径
	// 初始化数据
	for( v=0; v < G.numVertexes; v++ )
	{
		final[v] = 0;			// 全部顶点初始化为未找到最短路径
		(*D)[V] = G.arc[V0][v];		// 将与V0点有连线的顶点加上权值
		(*P)[V] = 0;			// 初始化路径数组P为0
	}
	(*D)[V0] = 0;		// V0至V0的路径为0
	final[V0] = 1;		// V0至V0不需要求路径
	// 开始主循环，每次求得V0到某个V顶点的最短路径
	for( v=1; v < G.numVertexes; v++ )
	{
		min = INFINITY;
		for( w=0; w < G.numVertexes; w++ )
		{
			if( !final[w] && (*D)[w]<min )
			{
				k = w;
				min = (*D)[w];
			}
		}
		final[k] = 1;	// 将目前找到的最近的顶点置1
		// 修正当前最短路径及距离
		for( w=0; w < G.numVextexes; w++ )
		{
			// 如果经过v顶点的路径比现在这条路径的长度短的话，更新！
			if( !final[w] && (min+G.arc[k][w] < (*D)[w]) )
			{
				(*D)[w] = min + G.arc[k][w];	// 修改当前路径长度
				(*p)[w] = k;			// 存放前驱顶点
			}
		}
	}
}

15、最短路径（弗洛伊德算法）

迪杰斯特拉算法是一个顶点到所有顶点的最短路径，但弗洛伊德算法是求所有顶点到所有顶点的最短路径。

#define MAXVEX 9
#define INFINITY 65535
typedef int Pathmatirx[MAXVEX][MAXVEX];
typedef int ShortPathTable[MAXVEX][MAXVEX];
void ShortestPath_Floyd(MGraph G, Pathmatirx* P, ShortPathTable* D) {
  int v, w, k;
  // 初始化D和P
  for (v = 0; v < G.numVertexes; v++)
    for (w = 0; w < G.numVertexes; w++) {
      (*D)[v][w] = G.matirx[v][w];
      (*P)[v][w] = w;
    }
  // 优美的弗洛伊德算法
  for (k = 0; k < G.numVertexes; k++)
    for (v = 0; v < G.numVertexes; v++)
      for (w = 0; w < G.numVertexes; w++)
        if ((*D)[v][w] > (*D)[v][k] + (*D)[k][w]) {
          (*D)[v][w] = (*D)[v][k] + (*D)[k][w];
          (*P)[v][w] = (*P)[v][k];  
        }
}

16、拓扑排序

一个无环的有相图称为无环图。

拓扑序列：设G=（V,E）是一个具有n个顶点的有向图，V中的顶点序列V1,V2，…,Vn满足若从顶点Vi到Vj有一条路径，则在顶点序列中顶点Vi必在顶点Vj之前。我们称这样的顶点序列为一个拓扑序列。

拓扑排序：所谓的拓扑排序，其实就是对一个有向图构造拓扑序列的过程。

拓扑排序算法：从AOV网中选择一个没有前驱的顶点（该顶点的入度为0）并且输出它;从网中删去该顶点，并且删去从该顶点发出的全部有向边;重复上述两步，直到剩余网中不再存在没有前驱的顶点为止。