声明: 仅个人小记
前言: 主要是引入一个新的看待矩阵乘法的角度觉得这个挺重要的,故做记录
列向量角度,矩阵左乘
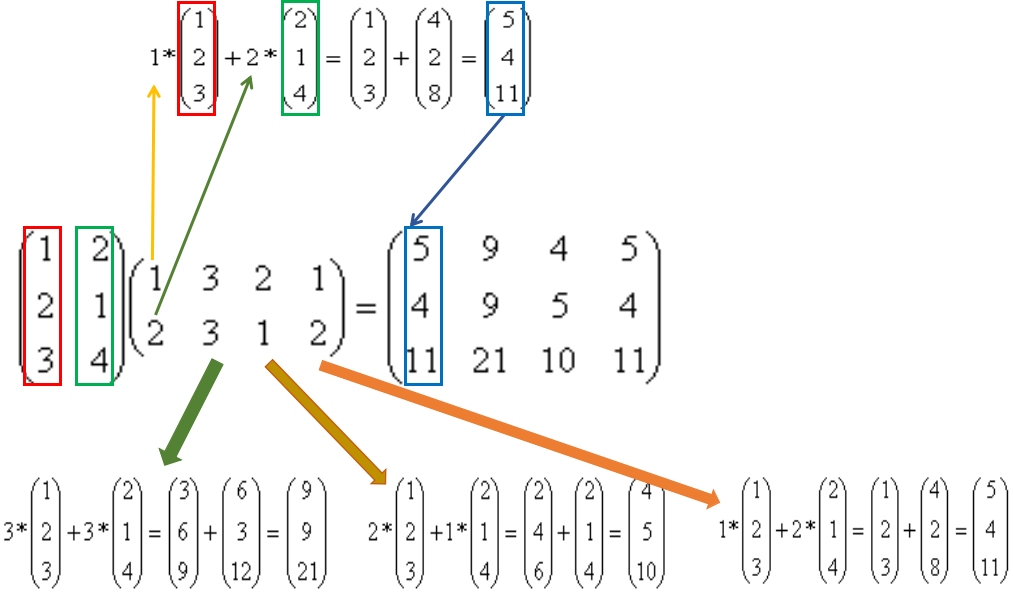
AB = C
结合上图,我们可以知道,结果矩阵C中的第 j 列完全可以表示为矩阵A中列向量的线性组合,具体怎样的线性组合完全是参看矩阵B中相应的第 j 列,与矩阵B中的其他列无关。
换言之,左侧矩阵提供基本的列向量,右侧的矩阵交代怎样的线性组合。
行向量角度,矩阵右乘
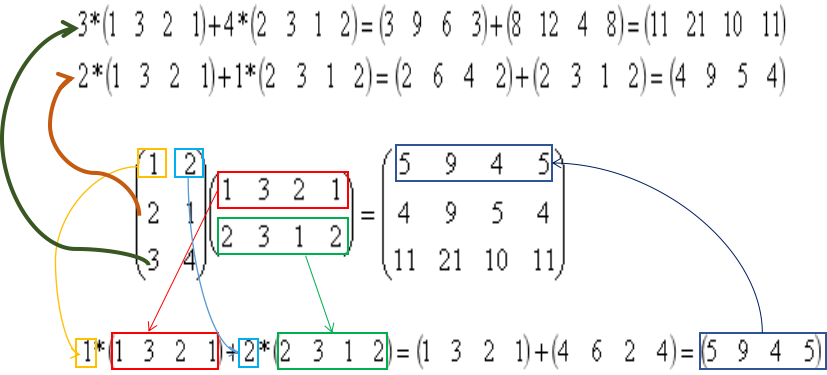
AB = C
结合上图,结果矩阵C中的第i行完全可以表达为矩阵B中的行向量的线性组合,具体如何进行线性组合,完全参看矩阵A中相应的第i行,与矩阵A中的其他行无关。
右侧矩阵提供基本的行向量,左侧矩阵交代进行怎样的线性组合,结果矩阵便是线性组合的结果。
根据上述讨论,解释两个定理
-
定理一
矩阵方程AX = B 有解的充分必要条件是R(A) = R(A,B)上面的总结可以很好的解释下面这个定理,即
R(A) : 矩阵A的秩
(A,B) :即两个矩阵水平按左右放在一起构成一个新的矩阵C。由上面知道,B中的每一列都可以表达为A中的列向量进行线性组合,所以**(A,B)中的B部分是可以通过初等变换被左边的A**完全消化,即,B的引入并没有树立新的独立的维度。
-
定理二
对于矩阵A,B , 有 R(AB) <= min{R(A),R(B)}
AB 是矩阵A和矩阵B的乘积结果,记作C。由上面的分析,可以知道,结果矩阵C中的所有向量都是可以表达为矩阵A的线性组合。我们可以进一步考虑C中能有多少个列向量呢?显然,结果矩阵C中的列向量的数目是由矩阵B的列数决定的。这里的讨论先暂停一下。
我们来讨论一下矩阵的秩,
- 矩阵的秩是可以看作是矩阵列(行)向量张成的空间的维度。
- 矩阵的秩 <= min{该矩阵行数,该矩阵列数}
- 从N维度空间中任意选出一组向量,以这组向量为基向量重新构建的空间的维度一定不会超过N。
- 从N维度空间中任意选出M个向量,以这组向量为基向量重新构建的空间的维度一定不会超过M。
所以,由于结果矩阵C中的列向量都是选自由矩阵A的列向量为基向量张成的空间。所以C中列向量张成的空间的维度一定不超过矩阵A的列向量张成的空间的维度,即矩阵A的秩。即得到 R(AB) = R© <= R(A)。
同样,我们再从行向量的角度看待AB。结果矩阵C中的行向量都是选自由矩阵B的行向量为基向量所张成的空间。所以结果矩阵C中行向量张成的空间的维度一定不超过矩阵B的行向量张成的空间的维度,即矩阵B的值。从而得到R(AB) = R© <= R(B)。
根据上述讨论,得到R(AB) <= {R(A),R(B)}








 本文提出了一种新的矩阵乘法理解方式,从列向量和行向量角度解析矩阵乘法,并通过直观的方式解释了两个关于矩阵方程解的存在性和矩阵乘积秩的重要定理。
本文提出了一种新的矩阵乘法理解方式,从列向量和行向量角度解析矩阵乘法,并通过直观的方式解释了两个关于矩阵方程解的存在性和矩阵乘积秩的重要定理。
















 3959
3959

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








