机器学习（二）概率密度分布之非参数估计

机器学习（二）概率密度估计之非参数估计

2018/2/19
by ChenjingDing

---

二.非参数估计

2.1直方图估计

直方图估计概率密度函数基本思想：
将数据空间分成许多个子空间，每一个子空间大小为$△$，在每一个子空间内计算样本出现的个数$n_i$，样本总个数为N，则概率密度函数为：

$$p(x) = \frac{n_i}{N△}；$$ 平滑因子：

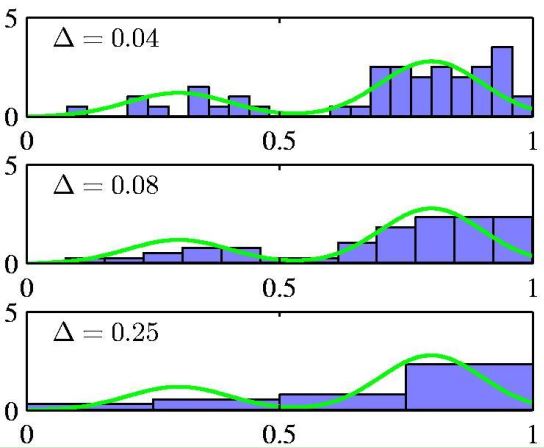
图4 不同平滑因子（上：平滑因子过小，估计的概率密度函数有很多毛刺，噪声； 中：平滑因子适合的时候，估计的概率密度函数； 下：平滑因子过大，估计的概率密度函数误差增大）

缺点：
当数据空间的维数为D，每一维划分的子空间个数为M，则所需子空间个数为$M^D$， 该个数呈指数级增长。有两种方法可以解决这个问题，它们都是针对每一个输入样本$\widehat{x}$，而并非对整个训练样本事先划分好子空间。
这两种方法有相同的思路：在一个很小的区域R内，

$$P(x) = \int _R p(x)dx \approx p(x)V \Rightarrow p(x) = \frac{P(x)}{V} = \frac{K}{NV}$$ K可以理解成V内训练样本的个数。如果固定V，则产生了核方法。如果固定K，则产生了K近邻估计的方法。

2.2核方法

引入核函数:

k(μ)⩾0,V=∫k(μ)dμ=1（积分也可不为1）则K(xˆ)=∑i=1nk(xi−xˆ)⇒p(x)=1N