矩阵
矩阵代表一个特定的线性变换
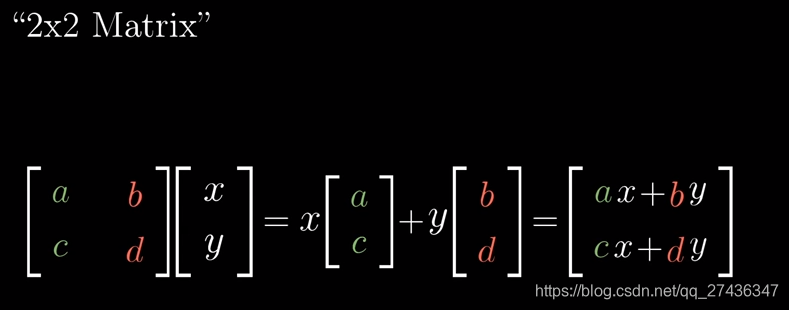
相当于用原来的scalars对新的基进行线性组合
非方阵
列空间的维数与输入空间的维数相等，即矩阵有几列说明输入空间的向量有几维（也等于基向量的个数）
行列式
数值代表面积（体积）的变化，符号代表空间是否被翻转。
行列式为0说明矩阵变换降维了，也说明矩阵不可逆，也表明会有一系列原来不是零向量的向量落到了零向量的位置，所有这些向量的集合构成了零空间
秩
列空间的维数
基变换
假设
A
A
A 为任意坐标系在正坐标系中的表示，
v
v
v为在任意坐标系中的scalars，
A
v
Av
Av得到的为正坐标系下该向量的坐标。
把正坐标系下的线性变换翻译成变换基的坐标系下的变换，比如要在新坐标系旋转90度，可进行
A
−
1
M
A
A^{-1}MA
A−1MA 线性变换，其中
M
M
M 为正坐标系下的旋转变换。
特征向量和特征值
特征向量就是经过线性变换后它仍然在经过它原先位置的直线，只是经过压缩或者拉伸，即
A
v
=
λ
I
v
Av=\lambda Iv
Av=λIv
(
A
−
λ
I
)
v
=
0
(A - \lambda I)v=0
(A−λI)v=0如果等式成立，并且有非0的v向量，则一定存在降维，所以
(
A
−
λ
I
)
(A - \lambda I)
(A−λI)的行列式应该为0，
873
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
