数学分析总复习

heine162

已于 2024-11-22 10:32:09 修改

阅读量791

点赞数 2

文章标签：算法

于 2023-10-23 11:15:02 首次发布

本文链接：https://blog.csdn.net/qq_27638851/article/details/133985015

版权

由于时间关系后续重新整理

前3章

确界存在定理，单调有界收敛（根据确界），夹逼准则，闭区间套，有界必有收敛子列（根据闭区间套），基本数列和柯西收敛原理（根据确界存在和有界必有收敛子列得出反例），压缩性原理（得出是基本数列）。海涅定理（假设不连续，取子列），函数的柯西收敛原理。闭区间连续必有界，最值定理，零点定理，中间值定理。一致收敛，一致连续的充要条件（假设非一致连续取子列），康托尔定理即闭区间连续必有一致连续（根据非一致连续），开区间一致连续的充要条件（当开区间一致连续时，取趋向端点的收敛子列，它是基本数列，同时它的函数也是基本数列根据heine定理知趋向于端点的极限存在）。复合函数的极限和反例。反函数的连续（用定义），求导。

若连续可考虑归结原则，致密性定理取子列，确界存在定理使用数列极限趋于上确界。

1.无穷远处极限存在，则一致连续

这是因为极限存在，则满足函数的柯西收敛原理（或者用趋向于无穷大时的heine定理）：

容易知道，函数在无穷大时，任意的两个点，函数值的差都趋向于0 ，那么判断一致连续时，它显然能保证缩小了点的范围，函数值的差还是趋于0的，因此肯定也是一致连续的。也就是说，函数在无穷大时极限存在，都不需要保证x1-x2的值是一个很小的范围，就能让f(x1)-f(x2)是无穷小量。

2. 最值定理

画圈的地方用到heine定理，没明说，想了好久。

3. 有限覆盖定理证明闭区间一致连续

有限个子集覆盖，意味着有限个邻域区间的交，这样取的x点也是有限个的，取区间的最小值，这样就保证该区间长度只和ξ和一个固定的点相关，固定的点看成常数，然后就能保证小于这个最小区间时，函数值相减小于ξ，同时取的领域满足 $\delta = \delta (\varepsilon )$ 而与x取哪个点无关。

4. 导函数极限定理

导数存在，导函数极限不一定存在（导函数不可能有跳跃间断点，因为有跳跃间断点的话，两边的极限值分别等于左右导数，与该点导数存在矛盾）。

函数存在原函数，但是函数不连续，如 $x^{2}sin\frac{1}{x}$ 的导数不连续，但是处处都有定义，其原函数为 $x^{2}sin\frac{1}{x}$ ， $x^{2}sin\frac{1}{x}$ 每一处都是可导的，如下图所示。

导数介值定理通过构造F(x) = f(x) + C，然后在某一点导数为0。

5. 递推公式求极限

6. 有界必有上确界，单调有界必收敛，且收敛于上确界。不收敛，则不是基本数列，则存在N，当m,n大于N时，xm-xn大于某个值

第5章微分中值定理及其应用（泰勒展开证明题合集-百度文库）

构造 $F(x) = f(x) - f(a) - \frac{f(b) -f(a)}{b-a}(x-a)$

对于泰勒公式而言，展开到一阶导数就是拉格朗日中值定理，展开到二阶导数常常用来证明二阶导数不等式，可以理解为关于二阶导数的中值定理：

此类题目常常是告诉你f(0)=0, f(1)=0，f(x0)处取最大值2这样的条件，然后让证明存在二阶导数大于等于4或者小于等于M。做法比较固定，就是在x=0，x=1处展成泰勒，然后两个等式相减，就可以得到二阶导数的范围。也就是说，证明导数的不等式，优先考虑泰勒公式，如果不等式中出现 $\frac{(a-b)^{2}}{4}$ 那么大概率是在（a+b）/2处展开，如果是3阶导数需要展开到第3阶等等。

琴森不等式：

用数学归纳法：1减去第k+1个数，然后均分给前面的k个数。

将函数 $f(x)=\sqrt{2+sinx}$ 在x=0处展开成皮亚诺余项的泰勒公式，需提取前面的2，若

$f(x)=\sqrt{2+sinx}=\sqrt{1+(1+sinx)}$ ，令u=1+sinx，然后在展开sinx时，当x趋于0时，u=1+sinx不在趋于0，这样带入到 $\sqrt{1+u}$ 时，u不趋于0，即o(u)和o(x)不是等价的，所以正确做法是：

$f(x)=\sqrt{2}\sqrt{1+\frac{sinx}{2}}$ ，这样x->0,sinx/2->0。将sinx展开和 $\sqrt{1+u}$ 分别展开，再讲sinx/2代入到 $\sqrt{1+u}$ 。

拉格朗日插值多项式：给定n+1个点x0，x1，...xn和它的函数值f(x0),...，那么可以求得一个n次多项式，它的函数值相等：

实际上，我们直接写出来更好理解，显然这样定义的pn(x)能够满足x0，x1等n个点，多项式pn(x)的函数值等于f(x0),f(x1),...

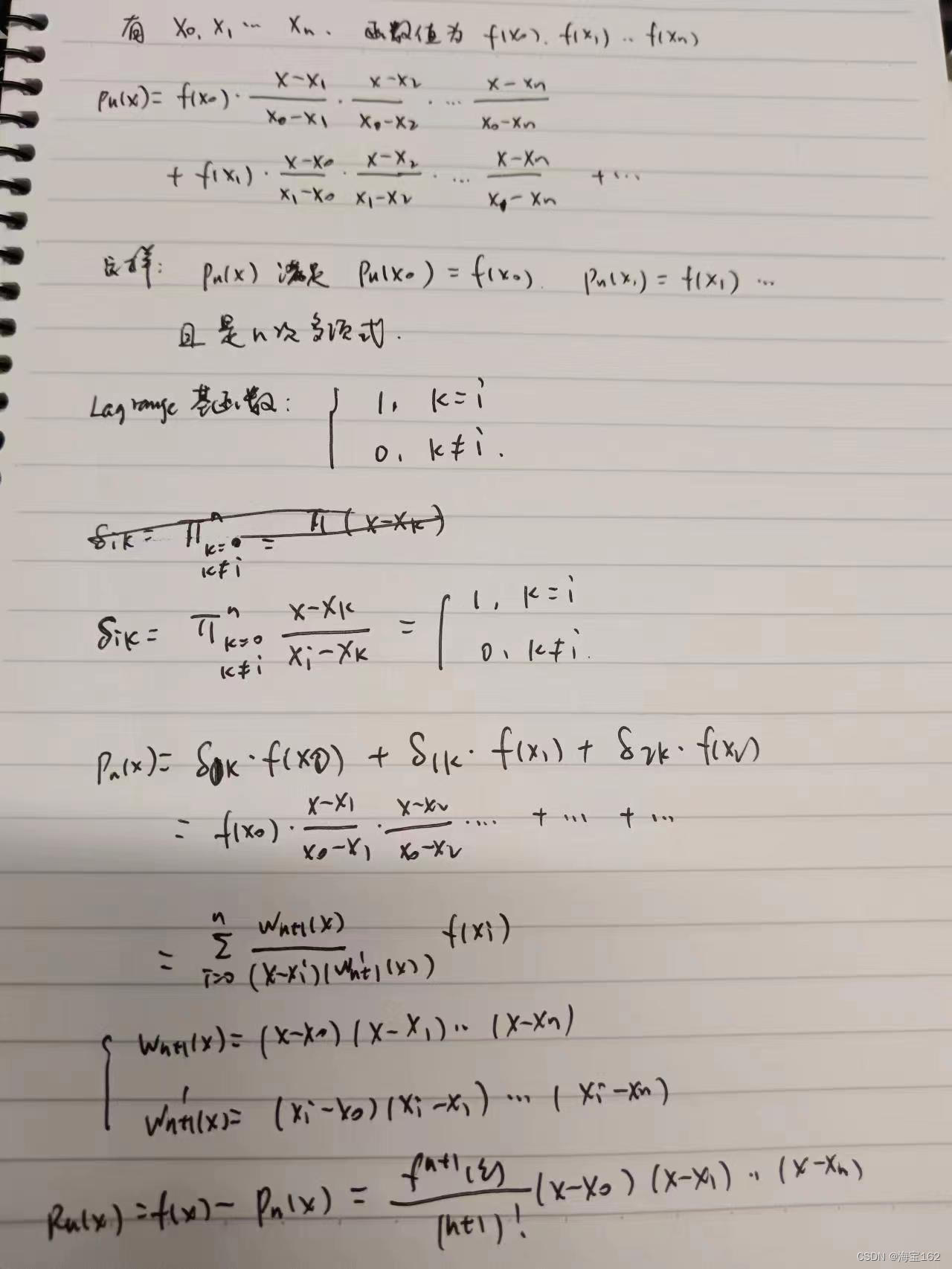
另一种是Taylor多项式，它是同一个点x0处，满足函数值和若干阶导数相等，比较简单不做叙述。

第6、7章不定积分和定积分

原函数：F(x)求导是f(x)。

可积：黎曼可积的简称，问可积，考虑的是闭区间，不要考虑反常积分。

1.函数有有限个间断点的话可积，但是没有原函数，因为这些间断点都不连续，更不可能在这些间断点处可导（可导必连续），即可积不代表有原函数。

2.函数有原函数，也不一定连续。如 $x^{2}sin\frac{1}{x}$ 的导数不连续，但是他的原函数是 $x^{2}sin\frac{1}{x}$ 。

3.f(x)连续，一定有原函数，积分上限函数就是其中的一个原函数，换一种说法就是此时积分上限函数存在连续的导函数f(x)，见课本积分上限函数。

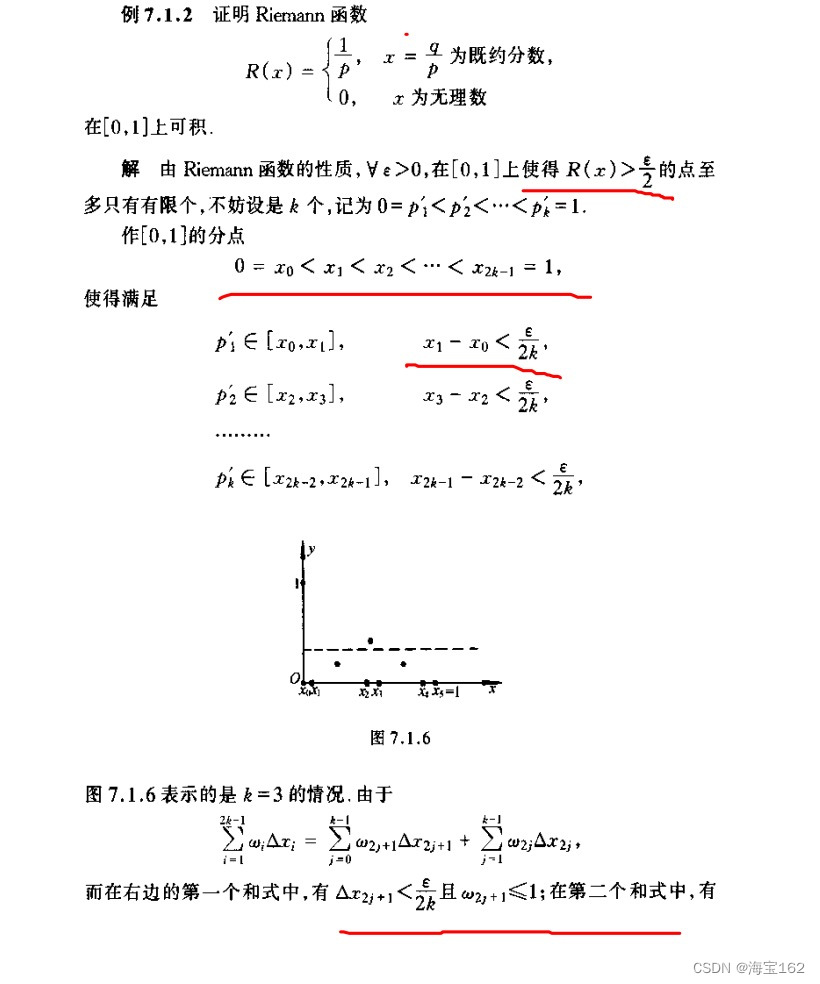
4.黎曼函数在有理点不连续，无理点连续，极限总是为0。黎曼函数是可积的：

5. 不可积，也会有原函数 ,例子暂缺

第10章函数项级数

极限和S(x)等于n趋向无穷大时，Sn(x)的极限，同时S(x)的每个点的值是每个S(x0)求出来以后，形成的曲线的值。

级数绝对收敛，则交换顺序还是收敛，收敛于同一个值，常常用来计算两个绝对收敛级数的乘积，他们等于柯西乘积。

第11章

聚点：任意领域包含属于S的无限多个点。内点和非孤立点的边界点都是聚点。

聚点都属于S，S为闭集。开集：全部是内点。

第12章曲面的法线和切平面方程（这一章要用上克莱姆法）

用两个参数(u,v)表示(x,y,z): x=x(u,v), y = y(u,v), z= z(u,v)。

z= z(u(x,y), v(x,y)), 考虑 F(x,y,z) = z(u(x,y), v(x,y)) - z = 0，F(x,y,z)=0的法向量是(Fx, Fy, Fz),从这个方向入手理解。

在求曲面面积时，曲面微元等于 $|r_{u}\times r_{v} |dudv$ ,即两个切向量的外积，来表示那块平行四边形面积，平行四边形面积等于边长a*边长b*他们的正弦值，又等于a和b外积的模，du和dv看成是长度，他们没有方向看成常数。

$r(u,v) = x(u,v)\mathbf{i} + y(u,v)\mathbf{j} + z(u,v)\mathbf{k}$

最后得到 $r_{u}\times r_{v}$ 因为垂直于这两个切向量，所以它是法向量，求出来正好也是12章参数方程求出来的法向量，它的模长再乘以dudv就是dS：

求向量积可以用行列式辅助计算：

最后计算的结果其实是需要进行转置，才能得到雅可比行列式的写法：

这个地方比较坑，差点把雅可比行列式都给弄错了，弄错了就完了，后面很多把曲面法向量写成雅可比行列式的。

当z=f(x,y)时，参数方程就是x = x,y = y

$r(x,y) = x\mathbf{i} + y\mathbf{j} + f(x,y)\mathbf{k},r_{x} = \mathbf{i} + f_{x}\mathbf{k},r_{y} = \mathbf{j} + f_{y}\mathbf{k}$

$|r_{x}\times r_{y}| = \begin{vmatrix} i & j & k \\ x _{u} & y _{u} & z_{u} \\ x _{v} & y _{v} & z _{v} \end{vmatrix} = \begin{vmatrix} i & j & k \\ 1 & 0 & f_{x} \\ 0 & 1 & f _{y} \end{vmatrix} = | -f_{x}\mathbf{i} - f_{y}\mathbf{j} + \boldsymbol{k}| = \sqrt{f_{x}^{2} + f_{y}^{2} + 1}$

第二类曲面积分：

cosa*dS = dydz而不是dxdy。dS投影到xoy面时，曲面和xoy面夹角等于法向量夹角，xoy面的法向量与z轴平行，为(0,0,1)。 dS的一个法向量为(-fx, -fy, 1)(如果是显示方程z=f(x,y))，单位向量为（cosa, cosb ,cosr）。所以dS和面xoy夹角的cos值等于dS的cosr值，所以cosr*dS = dxdy。同理cosa*dS = dydz, cosb*dS = dzdx，所以z=f(x,y)的曲面积分为：

$\iint_{\Omega }^{}P(x,y,z)dydz + Q(x,y,z)dzdx + R(x,y,z)dxdy = \iint_{\sum }^{}(P(x,y,z)cos\alpha + Q(x,y,z)cos\beta +R(x,y,z)cos\gamma )dS = \pm \iint_{\Omega }^{}(P(x,y,z)\frac{-fx}{\sqrt{fx^{2}+fy^{2}+1}} + Q(x,y,z)\frac{-fy}{\sqrt{fx^{2}+fy^{2}+1}}+R(x,y,z)\frac{1}{\sqrt{fx^{2}+fy^{2}+1}} )(fx^{2}+fy^{2}+1)dxdy$