第8章特征矩阵(矩阵相似、最小多项式、特征矩阵相似、不变因子、初等因子和若当标准型)

heine162

已于 2024-05-20 19:23:05 修改

阅读量7.6k

点赞数 10

文章标签：矩阵 1024程序员节

于 2023-09-11 10:14:33 首次发布

本文链接：https://blog.csdn.net/qq_27638851/article/details/132799949

版权

1.相似

相似有相同的特征多项式，相同的特征值，相同的迹，A的行列式即det(A)也相同，相同的最小多项式，相同的秩。

$tr(A) = tr(P^{-1}AP)$ 从而求A的迹（特征值）转化为另一个矩阵的迹（特征值）。

例：

（1）AB都正定，则tr(AB) > 0，A正定，则有可逆阵P:

$P^{T}AP = E\Rightarrow tr(AB) = tr(P^{T}AB(P^{T})^{-1}) = tr(P^{T}APP^{-1}B(P^{T})^{-1}) = tr(P^{-1}B(P^{T})^{-1}) = tr(P^{-1}B(P^{-1})^{T})$

由于B正定，所以特征值都大于0，所以AB的迹大于0。

（2）根据特征值的情况，判断矩阵可逆

若A的特征值为0和1，则|A - E| = 0，而A + E是可逆的，因为-1不是A的特征值，|A+E|不等于0，另外此时A+E特征值就是1，2，特别地，A的特征值为a则f(A)的特征值为f(a)。相应地,如果|A+aE| = 0,则 -a 就是A的一个特征值。

（3）矩阵相似于对角阵，可以求矩阵的幂：

$A^{n} = P^{-1}\Lambda PP^{-1}\Lambda PP^{-1}\Lambda P...=P^{-1}\Lambda ^{n} P$

若线性变换 $\AA$ 在一组基 $(\xi _{1},...,\xi _{n})$ 下的矩阵为A， $(\eta _{1},...,\eta _{n})$ 下的矩阵为B， $(\xi _{1},...,\xi _{n})$ 到 $(\eta _{1},...,\eta _{n})$ 的过渡矩阵为X，则 $B=X^{-1}AX$

下面讨论一下求线性变换的特征值和特征向量，如果他们选不同的基去求，结果有什么联系？

首先我们知道求特征值和特征向量的步骤如下：

如果换成另一组基的话，我们知道由于不同基下的矩阵相似，相似有相同的特征多项式，就会有相同特征值，那么特征向量还相等吗，事实上，选的基不同，那么基下的坐标可能就变了，但是线性空间的向量等于基乘以坐标，所以特征向量可能相等，下面证明，选的基不同，求的特征向量仍然是相同的：

这个书上也没有讲，主要是看到求特征向量时，书上说的是选一组基，既然是选那就是不唯一，所以就尝试证明了选不同基特征向量还是否相同。

2.最小多项式

满足 $f(A) = O$ 的最低次数的多项式。

$P^{-1}AP = B=>P^{-1}f(A)P = f(B)$

f(A)=0当且仅当f(B)=0。A和B相似，则有相同的最小多项式f(x)满足f(A)=0,f(B)=0。

根据汉密尔顿-凯莱定理：

$f(\lambda )=\left | \lambda E- A \right |=a_{n}x^{n} + ... + a_{0}\Rightarrow f(A) = a_{n}A^{n}+...+a_{0}E=0$

幂零矩阵的特征值只能是0，因为它的最小多项式满足 $\lambda ^{k}=0$ 。不过不一定可对角化，如果是对角线上的若当块的话。

最小多项式整除特征多项式。最小多项式相等不一定相似。

已知最小多项式，可以得出矩阵A若当标准型中，对角线都是A的特征值，若当标准型为对角矩阵，表示矩阵可对角化。若矩阵可对角化等价于则矩阵A的最小多项式为一次因式的乘积：

若当标准型存在若当块：

J = $\begin{pmatrix} a & & & \\ 1& \ddots & & \\ & \ddots & a & \\ & & 1 & a \end{pmatrix}$

J的特征多项式和最小多项式都为 $(\lambda - a)^{k}$ , k大于2，所以不可对角化意味着最小多项式有一个因式次数大于1。

最小多项式相同，不一定相似，如对角阵diag(1,1,2)和diag(1,2,2）。只有最小多项式可以知道若当矩阵的大概结构但需要分类讨论。特征多项式也一样，相同特征多项式也不一定相似，如上面的J和对角阵diag(a,a,a）都是 $(\lambda - a)^{k}$ ，但是一个是若当块，一个是对角阵。

3. 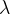$\lambda$ -矩阵

1.矩阵中的元素为 $\lambda$ 的多项式，即 $P[\lambda ]$ 的元素，称为 $\lambda$ -矩阵。

2. $A(\lambda)B(\lambda)=B(\lambda)A(\lambda)=E$ 则称 $A(\lambda )$ 可逆。

3. $A(\lambda )$ 可逆的充要条件是 $|A(\lambda )|$ 的值等于常数d：

$A(\lambda )$ 和 $B(\lambda )$ 都是多项式， $|A(\lambda )|$ 和 $|B(\lambda )|$ 相乘等于1，意味着 $A(\lambda )$ 和 $B(\lambda )$ 都是零次多项式，反过来， $|A(\lambda )|=d$ ，取 $B(\lambda )=\frac{A(\lambda )^{*}}{|A(\lambda )|}\Rightarrow \frac{A(\lambda )^{*}}{|A(\lambda )|}A(\lambda )=A(\lambda )\frac{A(\lambda )^{*}}{|A(\lambda )|}=E$ 。即 $|A(\lambda )|=d$ 可以得到 $A(\lambda )$ 可逆。

4. $A(\lambda )$ ， $B(\lambda )$ 等价，如果可以通过初等变换相互转化。

5.任意 $A(\lambda )$ 等价于标准型 $\begin{pmatrix} d_{1}(\lambda ) & & & & \\ & \ddots & & & \\ & & d_{k}(\lambda ) & & \\ & & & 0 \\ & & & & \ddots \end{pmatrix}$

其中 $d_{i}(\lambda )|d_{i+1}(\lambda ),i=1,...,k-1$ 。

证明： $A(\lambda )$ 至少有一个元素不能被 $a_{11}(\lambda )$ 元素除得尽，可以找到与 $A(\lambda )$ 等价的矩阵，左上角元素的次数低于 $a_{11}(\lambda )$ 。

由于次数最低为1，上述步骤不可能无限循环下去，因此能够将矩阵化成一个每个元素都能被 $a_{11}(\lambda )$ 元素除得尽的等价矩阵。（ $a_{ij}(\lambda )=a_{11}(\lambda ) \varphi ( \lambda )$ ）

再将第一行和第一列消去，化成一个左上角元素 $a_{11}(\lambda )$ 能除得尽 $A(\lambda )$ 中每一个元素的等价矩阵

$\begin{pmatrix} a_{11}(\lambda )& O \\ O & A_{1}(\lambda ) \end{pmatrix}$ 。

利用数学归纳法， $A_{1}(\lambda )$ 经过初等变换，可以将它的左上角 $a_{22}(\lambda )$ 能除得尽其中每个元素，且被 $a_{11}(\lambda )$ 除得尽的等价矩阵。最终变换为标准型。

6.k级子式的首相系数为1的最大公因式 $D_{k}(\lambda )$ 称为 $A(\lambda )$ 的k级行列式因子，若 $\lambda$ -矩阵等价，则具有相同的秩和各级行列式因子。

不改变的行和列，子式完全相同无须考虑。

第一种初等变换交换两行，交换的k级行列式的值只改变符号。第二种某一行乘以c倍，行列式结果相差c倍。前两种初等变换，他们的行列式因子显示是相同的。

第三种，将第j行乘以 $\varphi ( \lambda )$ 加到第i行，即 $a_{ik}(\lambda )=a_{jk}(\lambda ) \varphi ( \lambda )+a_{ik}(\lambda ),k=1,...n$ ，

不包含第j行的子式的结果为 $\begin{vmatrix} ... & & & \\ a_{i1}(\lambda ) +a_{j1}(\lambda )\varphi (\lambda ) & ... & & a_{in}(\lambda ) +a_{jn}(\lambda )\varphi (\lambda )\\ ...& & & \\ a_{k1}(\lambda ) & ... & & a_{kn}(\lambda ) \end{vmatrix}$

= $\begin{vmatrix} ... & & & \\ a_{i1}(\lambda ) & ... & & a_{in}(\lambda ) \\ ...& & & \\ a_{k1}(\lambda ) & ... & & a_{kn}(\lambda ) \end{vmatrix}$ + $\begin{vmatrix} ... & & & \\ a_{j1}(\lambda )\varphi (\lambda ) & ... & &a_{jn}(\lambda )\varphi (\lambda )\\ ...& & & \\ a_{k1}(\lambda ) & ... & & a_{kn}(\lambda ) \end{vmatrix}$

右边的都是原有矩阵的k级子式，它们的和都能除得尽k阶子式的公因式，所以第三种初等变换得到的矩阵k级行列式因子相等，k取遍1到n，各级行列式因子都相等。

由 $A(\lambda )$ 等价的标准型 $\begin{pmatrix} d_{1}(\lambda ) & & & & \\ & \ddots & & & \\ & & d_{k}(\lambda ) & & \\ & & & 0 \\ & & & & \ddots \end{pmatrix}$ 和初等变换不改变k级行列式因子，我们可以根据标准型的行列式因子计算 $A(\lambda )$ 的行列式因子，0能够被任何多项式除得尽，所以只需计算对角线上的k级子式的公因式，即行列式因子：

$D_{k}(\lambda )=d_{1}(\lambda )\cdots d_{k}(\lambda )$ ，反过来由 $d_{k}(\lambda )=\frac{ D_{k}(\lambda )}{ D_{k-1}(\lambda )}$ ，公因式是唯一的，所以 $D_{k}(\lambda )$ 都是唯一的，所以 $d_{1}(\lambda ),...d_{k}(\lambda )$ 都是唯一的。即标准型唯一， $d_{1}(\lambda ),...d_{k}(\lambda )$ 称为不变因子。

7.矩阵A与B相似的充要条件是 $\lambda E- A$ 和 $\lambda E- B$ 等价

若 $\lambda E- A=P_{0}(\lambda E- B)Q_{0}$ ，比较多项式的系数，可知 $P_{0}Q_{0}=E$ ， $A=P_{0}BQ_{0}$ 从而相似。

引理，看成多项式相除即可，即考虑多项式 $U(x)$ 除以 $x-a_{0}$ ,要么除尽，要么它的余数次数小于1，即余数为常数，商为次数小于 $U(x)$ 的多项式：

8.矩阵相似充要条件是特征矩阵 $\lambda E- A$ 和 $\lambda E- B$ 等价（即能够初等变换相互转化），特征矩阵相似的充要条件是行列式因子和不变因子完全相同（充分性是因为初等变换不改变行列式因子，必要性：若不变因子相同，说明两个特征矩阵都能初等变换为同一个标准型，实际上标准型也能初等变换为矩阵A,B，因为A和B标准型相同也就等价，等价有传递性）。

因此，矩阵相似的充要条件也可以认为它们的特征矩阵有相同的不变因子。

特征矩阵 $|\lambda E- A|$ 的值为多项式不为0，因此秩为n，标准型中一定有n个不变因子，它们的乘积等于 $|\lambda E- A|$ 。等价相当于乘以初等矩阵，所以 $\lambda E- A=P_{1}...P_{s}\Lambda Q_{1}...Q_{k}$ ， $\Lambda$ 为标准型 $\lambda$ 矩阵，即特征矩阵和标准型等价由于初等矩阵的秩全为1，所以 $|\lambda E- A|=|\Lambda |$

显然特征多项式也等于n级行列式因子因此给出不变因子 $D_{n}(\lambda )=d_{1}(\lambda )\cdots d_{n}(\lambda )$ ，有了不变因子就可以求得特征多项式。

9.初等因子

次数大于0的不变因子，分解成首项系数为1的一次因式方幂的乘积，这些一次因式方幂是初等因子，相同按次数计算。

根据定义，不变因子确定了，初等因子就确定了。反过来，初等因子相同，将相同因式按照升幂的方式填入标准型中（初等因子是从其中一个不变因子的因式分解中取出来的，所以每一个初等因子一定在某一个不变因子里），考虑这些初等因子在标准型矩阵的位置：

最高次在最后一个不变因子中，次高次数在倒数第二个位置，往后类推，数量不够的因式补适当个1，所有的初等因子填完，就能够唯一确定标准型和不变因子。

所以不变因子相同等价于初等因子相同，因此矩阵和矩阵相似又等价于和这个矩阵有相同初等因子。这里的矩阵是数字矩阵，数字矩阵的行列式是特征多项式，所以最高次数出现在对应的特征矩阵的右下角，但并不是任何 $\lambda$ -矩阵可以认为初等因子相同能唯一确定标准型：

10、求若当矩阵的初等因子，若已知矩阵A的初等因子，则可以确定A相似于有相同初等因子的若当矩阵。

对角形矩阵将相邻位置的相同因式交换位置，得到的矩阵和对角矩阵等价：

1. f1(x)和g1(x)互素，则(f1(x),f2(x))和(g1(x),g2(x))的公因式d1(x),d2(x)互素。

这是因为假如d1(x),d2(x)不互素(d1(x)整除f1(x),f2(x)，d2(x)整除g1(x),g2(x))，就存在一个次数大于0的多项式d3(x),它整除d1(x),d2(x)，当然也整除f1(x),f2(x),g1(x),g2(x)。即d3(x)是f1(x)和g1(x)的公因式。与f1(x)和g1(x)矛盾。

2. d1(x)互素和d2互素，又能整除d(x),则d1(x)d2(x) | d(x)用到了多项式中的性质二。

3. d(x) | f1(x)g1(x)则可以找到f(x)和g(x)使d(x)=f(x)g(x),且f(x) | f1(x), g(x) | g1(x)

对角矩阵的某一个相邻子式等价，则两个矩阵也等价（和矩阵正定的充要条件为顺序主子式都大于0证明过程差不多）：

最后得到的等价的对角阵，主对角线上的相同一次因式的方幂是升幂排序,为其标准型。这些一次因式都是标准型的初等因子，也是原来的对角形矩阵的初等因子。

求矩阵的初等因子：

1.求和它相似的若当矩阵或者对角阵的初等因子，对角线上的一次因式的方幂就是所求的初等因子。反过来，已知矩阵的初等因子，可求得若当矩阵。

2. 特征矩阵化成标准型，从不变因子中找出初等因子，推算出若当矩阵的每个若当块，这样他们有相同初等因子，意味着矩阵总是可以相似于若当矩阵。若当矩阵中按照特征值划分，若当块为k阶方阵时，有一个k-1级行列式因子为1，k级行列式为 $(\lambda - a)^{k}$ ，k全部等于1，意味着矩阵就可以对角化，即初等因子的一次因式的次数全部为1。这样矩阵由于相似于该若当矩阵，他们特征值就相同。因此a就是其中一个特征值。