Locating and Editing Factual Associations in GPT翻译

摘要

我们分析了自回归transformer语言模型中事实相关的存储和召回，发现了这些相关事实能够被定位，且可以直接编辑计算的证据。我们首先提出了一种因果干预方法来识别模型中对事实预测具有决定性的神经元激活。这揭示了中层前馈模块中的一组独特步骤，这些模块在处理主观字符时处理了事实预测。为了测试我们的假设，即这些计算对应于事实相关的召回，我们使用Rank-One Model Editing (ROME)修改了前馈模块的权重，以更新特定的事实。我们发现ROME在标准的zero-shot关系提取（zsRE）模型编辑任务上是有效的。我们还在一个具有较难的反事实断言的新数据集中评估了ROME，表明该方法保持特异性和泛化性，而其他方法则会牺牲其中一种。我们的结果证实了中层前馈模块存储事实的重要作用，并表明直接操纵计算机制可能是进行模型编辑的可行方法。代码，数据集，可视化和交互式演示笔记可在https://rome.baulab.info/上找到。

1.介绍

　　大型语言模型将事实存储在哪里？在本文中，我们报告的证据表明，GPT中的事实对应于可以直接编辑的局部计算。
　　大型语言模型可以预测世界相关的事实描述。例如，给定“The Space Needle is located in the city of”的前缀，GPT能可靠地预测出真正的答案：“Seattle”（图1a）。已经观察到在自回归GPT模型和屏蔽BERT模型中都出现了事实知识。
　　在本文中，我们研究了这些种事实是如何存储在类似GPT的自回归transformer模型中的。尽管目前使用的许多大型神经网络都是自回归的，但他们存储知识的方式仍然未被探索。目前一些研究主要针对针对屏蔽语言模型，但是GPT这种结构差异，例如单向注意力和生成能力，为新的观点提供了方向。
　　我们使用了两种方法：
　　首先，我们使用因果干预分析来追踪GPT中隐藏状态激活的因果关系，以识别与主题事实相关的具体模块（图1）。我们的分析表明，在处理主题名称的最后一个字符时，一系列中间层的前馈MLP具有决定性作用（图1b,2b,3）。
　　其次，我们通过引入Rank-One Model Editing方法（ROME）来改变模型权重以测试这一发现，以更改确定决定性字符的前馈层行为的参数。尽管干预很简单，但我们发现ROME与标准zero-shot关系提取基准的其他建模方法相似（第3.2节）。
　　为了评估ROME对更困难案例的影响，我们引入了一个反事实断言的数据集（第3.3节），这是在训练集中尚未出现的。我们的评估（第3.4节）证明，中间层MLP模块可以存储具有较强泛化能力的事实，同时仍然和特定主题相关联。与以前的微调，基于可解释性和元学习方法相比，ROME同时实现了良好的泛化性和特异性，而先前的方法总会牺牲了其中一种。

2.Interventions on Activations for Tracing Information Flow

为了在较大预训练自回归transformer的参数中定位事实，我们首先分析和识别对单个事实预测具有强烈因果影响的特定隐藏状态。我们将每个事实表示为一个知识元组$t=(s,r,o)$，其中包含主题$s$，目标$o$和连接两者的关系$r$。然后，为了引出GPT中的事实，我们提供了一个自然语言提示$P$来描述$(s,r)$并检查模型的预测$o$。
　　自回归transformer语言模型$G:\mathcal{X}\to \mathcal{Y}$在词汇$\mathcal{V}$上映射一个字符序列$x=[x_1,...,x_T]\in \mathcal{X}$，其中$x_i\in \mathcal{V}$变换到$x$中下一个连续字符的概率分布$y\in \mathcal{Y}\subset {\mathbb{R}}^{|V|}$。在transformer中，第$i$个token被嵌入为一系列隐藏状态向量$h_i^{(l)}$，并从$h_i^{(0)}=emb(x_i)+pos(i)\in {\mathbb{R}}^H$开始。最终的输出$y=decode(h_T^{(L)})$是从最后一个隐藏状态读取的。
　　我们将$G$内部隐藏状态$h_i^{(l)}$的计算可视化为网格（图1a），其中每一层$l(left\to right)$添加了全局注意力$a_i^{(l)}$和局部MLP $M_i^{(l)}$，用于对上一层的输出进行计算。回想一下，在自回归情况下，当前字符仅从历史字符获取信息：
$$\begin{array}{c}{h}_i^{(l)}=h_i^{(l-1)}+a_i^l+m_i^{(l)}\\ a_i^l=att{n}^{(l)}(h_1^{(l-1)},h_2^{(l-1)},...,h_i^{(l-1)})\\ m_i^{(l)}=W_{proj}^{(l)}\sigma (W_{fc}^{(l)}\gamma (a_i^{(l)}+h_i^{(l-1)})).\end{array}\text{\hspace{1em}(1)}$$
每一层的MLP是由矩阵$W_{proj}^{(l)}$和$W_f^{(l)}c$参数化的双层神经网络，且具有修正非线性$\sigma$和非线性归一化$\gamma$。有关transformers的详细背景，请参考Vaswani et al. (2017)。

2.1 Causal Tracing of Factual Associations

状态网格（图1）构成了一个因果图，描述了隐藏变量之间的依赖性。该图包含许多从左侧的输入到右下输出的路径，我们希望了解到是否有特定的隐藏状态变量在召回事实时比其他变量更重要。
　　如Vig et al. (2020b) 所表明的，这是因果干预分析（causal mediation analysis）的自然场景，它量化了因果图中中间变量的贡献。为了计算每个状态对正确事实预测的贡献，我们进行三次运行以观察$G$中的所有内部激活：（1）clean run，（2）corrupted run，（3）corrupted-with-restoration run。

• 在clean run中，我们将事实提示$x$传递到$G$中，并收集所有隐藏的激活 { h i ( l ) ∣ i ∈ [ 1 , T ] } \{h^{(l)}_i|i\in [1,T]\} {hi(l)​∣i∈[1,T]}。图1a提供了一个提示的样例：“The Space Needle is in downtown __”，期望的输出是$o=$“Seattle”。
• 在基线corrupted run中，该主题在运行网络$G$之前需要进行混淆。具体地，将$x$嵌入为$[h_1^{(0)},h_2^{(0)},...,h_t^{(0)}]$后，我们对主题实体所对应索引$i$上的嵌入设置$h_i^{(0)}:=h^{(0)}i+ϵ$，其中$ϵ\sim \mathcal{N}(0;v)$。 然后正常运行$G$，从而得到一组破坏的激活 { h i ∗ ( l ) ∣ i ∈ [ 1 , L ] , l ∈ [ 1 , L ] } \{h^{(l)}_{i*}|i\in[1,L],l\in[1,L]\} {hi∗(l)​∣i∈[1,L],l∈[1,L]}。由于G失去了一些有关主题的信息，因此它可能会返回错误的答案（图1b）。
• 在corrupted-with-restoration run中，类似于corrupted run，除了一些token $\hat{i}$和层$\hat{l}$，令$G$在噪声嵌入上进行计算。在那里，我们勾住G，以迫使它后续输出干净的状态$h_{\hat{i}}^{(l)}$。未来的计算的执行则无需进一步干预。直观地，尽管有许多其他状态被混淆的主题破坏了，但少数干净状态对恢复正确事实的能力将表明它们在计算图中的因果重要性。

令$\mathbb{P}[o]$，${\mathbb{P}}_{\ast }[o]$以及${\mathbb{P}}_{\ast ,clean{h}_i^{(l)}}[o]$分别表示在干净，破坏和破坏加恢复情况下输出$o$的概率。上述表示为了简单，省略了输入$x$的符号。total effect (TE)是这些值之间的差异：$TE=\mathbb{P}[o]-{\mathbb{P}}_{\ast }[o]$。特定干预状态$h_i^{(l)}$的indirect effect(IE) 被定义为破坏版本下$o$的概率与该状态设置为干净版本时$o$概率之间的差异，同时该主题仍然被破坏：$IE={\mathbb{P}}_{\ast ,clean{h}_i^{(l)}}[o]-{\mathbb{P}}_{\ast }[o]$。对语句样本进行平均，我们就获得了每个隐藏状态变量的平均总效应（ATE）和平均间接效应（AIE）。

2.2 Causal Tracing Results

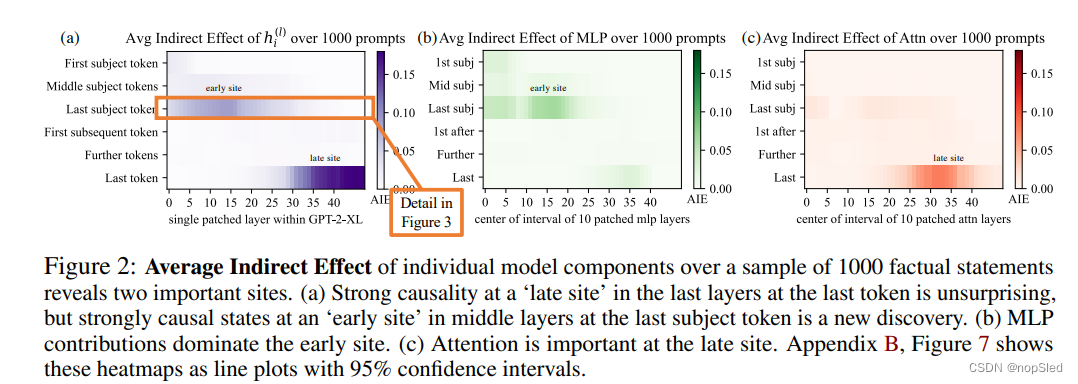
　　我们通过改变句子中的不同位置和不同的模型组件（包括各个状态，MLP层和注意力层）的干预，计算了超过1000个事实语句的平均间接效应（AIE）（附录B.1中的详细信息）。图2绘制了GPT-2 XL（1.5B参数）内部的AIE。该实验的ATE为18.6％，我们注意到，很大一部分效应是由最后一个主题字符上的因果状态导致的（15层的AIE=8.7％）。在最后一个主题字符存在较强的因果状态并不奇怪，但是它们出现在该主题最后一个字符的前几层是一个新发现。
　　通过分解MLP和注意力模块贡献的因果关系（图1 fg和图2 bc）表明，前面几层的MLP模块起决定性作用：MLP贡献峰值为6.6％，而最后一个主题字符的注意力效应仅为AIE 1.6％。在提示的最后一个字符上，注意力更为重要。附录B.2进一步讨论了这种分解。
　　最后，为了更清楚地了解MLP层在前面几层的特殊作用，我们使用一个修改的因果图分析了间接效应（图3）：（a）首先，我们在基线条件下使用破坏的输入收集了每个MLP模块的贡献。（b）然后，为了隔离MLP模块在测量因果效应时的效果，我们将计算图修改以切断字符$i$处MLP的计算，并在基线损坏的状态下固定它们，以免它们受到感觉状态$h_i^{(l)}$插入的影响。这种修改是一种避免MLP计算的探测path-specific effect的一种方法。（c）将修改图中的平均间接效应与原始图中的平均间接效应进行比较，我们观察到（d）在没有激活未来MLP模块时，最低层失去了因果效应，而（f）较高层状态的效应很少取决于MLP。当切断注意力模块以进行比较时，啧没有看到这种过渡。该结果证实了（e）MLP模块在回忆事实时起重要作用。
　　附录B展示了在其他自回归模型和实验设置上具有相似的结果。特别是，我们发现因果追踪比基于梯度的方法（例如integrated
gradients）更具信息性（图16），并且在不同的噪声配置下是可靠的。
　　因此问哦们认为部分中间层的MLP具有召回主题事实的能力。

2.3 The Localized Factual Association Hypothesis

基于因果追踪，我们提出了一种用于存储事实的特定机制：每个中间层的MLP模块接受编码了主题的输入，然后产生输出，从而召回有关该主题的属性。中层MLP的输出积累信息，然后通过高层注意力将信息求和复制到最后一个字符。
　　该假设将事实沿三个维度定位，将事实存储在（i）MLP模块的（ii）特定层，特别是（iii）在主题最后一个字符的处理中。这与Geva et al. (2021) 认为MLP存储知识的观点一致，而Elhage et al. (2021) 研究显示了自注意力的信息复制作用。此外，Zhao et al. (2021) 发现可以与行为的最小变化交换transformer层顺序。也就是说，在中间范围内的单个层的特定选择或布置没有其他特殊作用。我们猜想，任何事实都可以等效地存储在任何中间MLP层中。为了检验我们的假设，我们将关注点缩小到中间层$l^{\ast }$的单个MLP模块，并查看是否可以显式修改其权重以存储任意事实。

3.Interventions on Weights for Understanding Factual Association Storage

　　尽管因果追踪发现了MLP模块负责召回事实，但我们也希望更进一步了解如何将事实存储在MLP权重中。Geva et al. (2021) 观察到MLP层（图4 cde）可以作为两层的键-值存储器，其中第一层$W_{fc}^{(l)}$的神经元形成一个键，第二层$W_{proj}^{(l)}$检索该键关联的值。我们假设MLP可以建模为线性关联存储器。请注意，这与Geva等人的per-neuron观点不同。
　　我们通过进行一项新的干预方式来检验这一假设：使用Rank-One Model Editing (ROME)来修改事实。其能够插入一个新的知识元组$t^{\ast }=(s,r,o^{\ast })$以代替当前元组$t^c=(s,r,o^c）$，同事具有泛化性和特异性，这能够证明关联存储机制的细粒度理解。

3.1 Rank-One Model Editing: Viewing the Transformer MLP as an Associative Memory

我们将$W_{proj}^{(l)}$看作线性关联存储器。从该视角可以观察到，任何线性操作$W$可以作为使用一组键向量$K=[k_1|k_2|...]$和对应值向量$V=[v_1|v_2|...]$的键值存储操作，以求解$WK\approx V$，其均方误差使用Moore-Penrose pseudoinverse来最小化：$W=V{K}^{+}$。Bau et al. (2020) 观察到，可以通过求解约束最小二乘问题来最优地插入新的键-值对$(k_{\ast },v_{\ast })$。在卷积网络中，Bau等人使用该优化解决此问题，但是在全连接层中，我们可以得出一个闭式解：
$$minimize||\hat{W}K-V||suchthat\hat{W}{k}_{\ast }=v_{\ast }bysetting\hat{W}=W+\Lambda (C^{-1}{k}_{\ast }{)}^T.\text{\hspace{1em}(2)}$$
其中$W$是原始矩阵，$C=K{K}^T$是一个常数，我们通过估算来自Wikipedia文本样本的$k$的协方差（附录E.5），且$\Lambda =(v_{\ast }-W{k}_{\ast })/(C^{-1}{k}_{\ast }{)}^T{k}_{\ast }$是原始存储矩阵上与新键-值对的残差成正比的矢量（完整推导可查看附录A）。由于这种简单的代数结构，我们可以直接插入任何事实$(k_{\ast },v_{\ast })$。剩下的就是选择适当的$k_{\ast }$和$v_{\ast }$。
　　Step 1: Choosing k∗ to Select the Subject。
　　Step 2: Choosing v∗ to Recall the Fact。
　　Step 3: Inserting the Fact。