Satori: Reinforcement Learning with Chain-of-Action-Thought Enhances LLM Reasoning翻译

摘要

大语言模型 (LLM) 已在不同领域展现出卓越的推理能力。最近的研究表明，增加测试时计算可增强 LLM 的推理能力。这通常涉及在外部 LLM verifier的指导下在推理时进行大量采样，从而形成 two-player 系统。尽管有外部指导，但该系统的有效性证明了单个 LLM 解决复杂任务的潜力。因此，我们提出了一个新的研究问题：我们能否内化搜索能力，从根本上增强单个 LLM 的推理能力？这项工作探索了一个正交方向，重点关注训练后 LLM 的自回归搜索（即具有自我反思和自我探索新策略的扩展推理过程）。为了实现这一目标，我们提出了行动-思维链 (Chain-of-Action-Thought, COAT) 推理和一个两阶段训练范式：1) 小规模格式微调阶段，以内化 COAT 推理格式；2) 利用强化学习的大规模自我改进阶段。我们的方法产生了 Satori，一个基于开源模型和数据进行训练的 7B LLM。大量的实证评估表明，Satori 在数学推理基准上实现了最先进的性能，同时在领域外的任务中表现出很强的泛化能力。代码、数据和模型将完全开源。

1.介绍

大语言模型 (LLM) 在各种推理任务中都表现出色，包括数学问题、编程和逻辑推理。实现这些强大推理能力的关键技术之一是思维链 (CoT) 提示，它允许 LLM 通过生成一系列中间推理步骤来解决复杂任务。因此，许多早期的努力都集中在使用大规模、高质量的 CoT 推理链对 LLM 进行微调，无论是通过人工标注还是通过从更高级的模型中提取合成数据。然而，人工标注极其耗费人力，而蒸馏通常会将模型的推理能力限制到一定水平。
　　除了扩大训练资源外，最近的研究还集中在测试时扩展上，即分配额外的推理时间计算来搜索更准确的解决方案。这通常涉及大量采样，要么生成多个完整解决方案，要么采样多个中间推理步骤。这些方法通常需要外部反馈来指导搜索过程，通常是通过训练辅助奖赏模型来评估最终解决方案或中间步骤。然而，这种 two-player 框架会产生更多的模型部署成本，并且无法将搜索功能内化到单个 LLM 中。
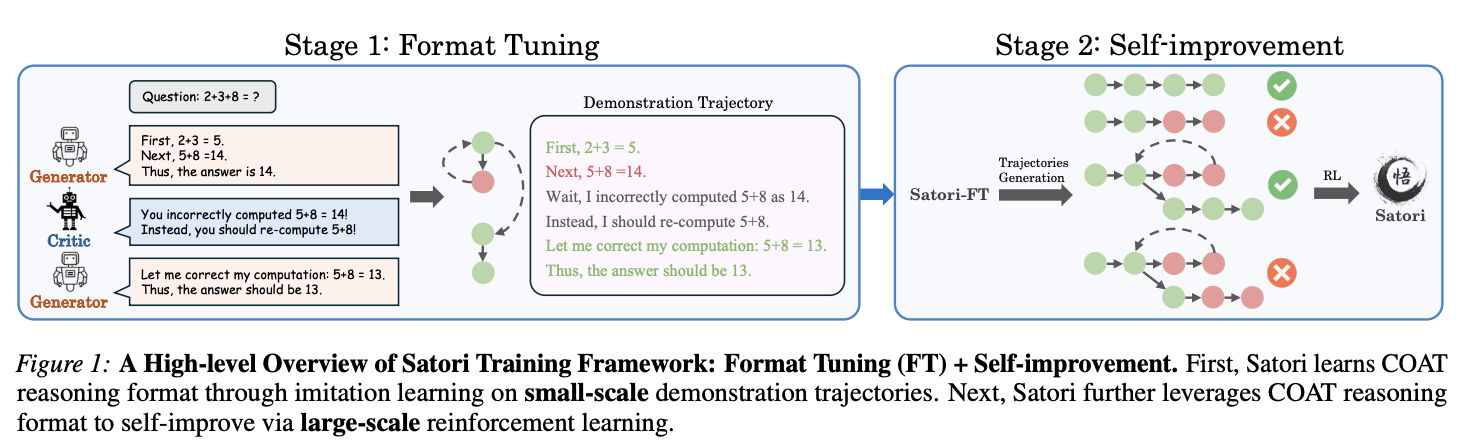
　　与上述工作正交的是，我们的研究探索了一个新方向，使 LLM 具有自回归搜索功能，即具有自我反思和自我探索新策略的扩展推理过程。具体来说，我们引入了行动-思维链 (Chain-of-Action-Thought, COAT) 机制，使 LLM 能够在解决问题时采取各种元行动。与由大规模有监督微调 (SFT) 和从人类反馈中强化学习 (RLHF) 组成的传统后训练不同，我们提出了一种新的两阶段训练范式：(1) 小规模格式微调 (FT) 阶段，以内化 COAT 推理格式；(2) 大规模自我改进阶段，利用强化学习和“重启和探索”(RAE) 技术。我们的方法促成了 Satori 的开发，这是一个 7B LLM，在开源基础模型和数学数据上进行训练，在领域内和领域外任务上均取得了卓越的表现。总而言之，我们的贡献有三方面，

1. Efficiency。Satori 是一个单一的 LLM，能够在没有外部指导的情况下进行自回归搜索（第 6 节和第 A 节）。而且，这是通过最少的监督和大规模的自我改进实现的。
2. Effectiveness。Satori 在领域内数学推理任务中表现出优异的性能，并且优于基于相同 base 模型构建的指令模型（第 5.1 节）。
3. Generalizability。与最近的数学推理研究不同，Satori 表现出对领域外任务的强大可迁移性，并展示了自我反思和自我探索的通用能力（第 5.2 节）。

2. Related Work

我们总结了与本文范围密切相关的文献（更多讨论请参阅 B 部分）。
　　Concurrent Work。基于 OpenAI o1 的影响，研究界做出了巨大努力，以增强具有高级推理能力的开源 LLM。最常见的方法依赖于从更强大的教师模型中提取知识。相比之下，Satori 从强化学习 (RL) 的角度解决了这个问题，并且只需要最少的有监督数据（格式微调阶段仅需 10K 个样本）。最相关的并行工作是 DeepSeek 最近发布的 R1，它采用了类似的高级策略，即小规模冷启动 SFT，然后进行大规模 RL 训练。虽然这两项工作在这个高级思想上是一致的，但我们的工作在关键方法上与 R1 不同，包括数据合成框架和 RL 算法。此外，DeepSeek-R1 专注于训练大规模 LLM（671B），而我们的工作为开发用于研究目的的小规模 LLM（7B）提供了见解。最后，作为业界开发的模型，DeepSeek-R1 的技术细节尚未完全公开，因此很难复制，而我们的工作是一项完全透明的研究，旨在开源训练数据和训练方案。
　　Post-training LLMs for Reasoning。最近的进展集中在广泛的后训练上，以增强推理能力。一些研究专注于构建高质量的指令微调数据集，但标注成本昂贵。最近的研究集中在自我改进方法上，其中模型使用自己生成的数据进行训练。此外，强化学习方法，特别是基于近端策略优化 (PPO) 的方法，已被证明更有效，它们通常利用奖赏模型来指导学习过程。
　　Enabling LLMs with Searching Abilities。基于提示的方法引导 LLM 通过纠错和探索替代路径来寻找解决方案。然而，这种方法不能从根本上增强 LLM 的推理能力。此外，最近的研究指出了 LLM 在自我纠正方面的困难。最近的研究转向训练 LLM 进行自我探索。一些研究专注于实现轨迹级搜索——迭代地识别以前完整响应中的错误并产生改进的响应。另一条研究路线探索了步骤级搜索，这使 LLM 能够以更细粒度的方式识别和纠正错误。一些人使用另一个模型提供步骤级反馈来实现这一点，但这种 two-player 框架的模型部署成本很高。SoS 是另一项密切相关的工作，它试图训练单个 LLM 以扁平字符串的形式执行树搜索。然而，SoS 的有效性主要体现在简单的符号任务上，其推广到更复杂问题的能力仍有待探索。

3. Preliminaries

我们通过训练语言模型 ${\pi }_{\theta }$ 来解决数学问题，给定问题提示 $\text{x}$，生成与基本事实 ${\text{y}}^{\ast }$ 匹配的解决方案 $\tilde{\text{y}}$。所有序列 $\text{x},\text{y}$ 和 ${\text{y}}^{\ast }$ 都由预定词表中的 token 组成。由于我们的方法使用强化学习 (RL) 来训练解决数学问题的模型，我们在下面概述了关键的 RL 概念。
　　Reinforcement Learning (RL)。RL 涉及 Agent 通过与环境的交互做出连续决策，以最大化期望累积奖赏。在这里，语言模型 ${\pi }_{\theta }$ 充当 Agent 的策略。从初始状态 $z_0$ 开始，在每个步骤 $l$，Agent 观察当前状态 $z_l$，获得奖励 $r_l$，根据 ${\pi }_{\theta }$ 选择动作，转换到下一个状态 $z_{l+1}$，并继续直到到达终止状态。轨迹是此交互过程中的状态和动作序列。RL 优化策略以最大化期望奖赏 ${}^{\prime }{\sum }_{l=1}^L{r}_l$，其中 $L$ 是轨迹长度。

4. Method

　　本节我们将介绍推理的形式，以及如何将推理形式化为一个序列决策问题。Goal：我们希望训练 LLM 通过多步骤推理来解决问题，而不是直接预测最终答案。给定问题陈述 $\text{x}$，模型将生成一系列推理步骤 { y 1 , y 2 , . . . , y L } \{\textbf y_1, \textbf y_2, . . . , \textbf y_L\} {y1​,y2​,...,yL​}，其中 ${\text{y}}_L$ 提供最终答案。但是，并非所有中间步骤都有用——重复错误并不能提高准确性。有效的推理需要验证正确性、识别错误并考虑替代解决方案。例如，给定 $x=“1+1=?”$，模型可能最初输出 ${\text{y}}_1=3$，然后在 ${\text{y}}_2$ 识别到错误（例如，“Wait, let me verify…””），然后将其更正为 ${\text{y}}_3=2$。
　　Chain-of-Action-Thought reasoning (COAT)。关键挑战是让模型能够在没有外部干预的情况下确定何时反思、继续或探索替代方案。为了实现这一点，我们引入了特殊的元操作 token，用于指导模型的推理过程，而不仅仅是标准文本生成。这些 token 可作为提示，让模型在继续之前确定何时重新评估其推理。

• Continue Reasoning (<|continue|>)：鼓励模型通过生成下一个中间步骤来构建其当前的推理轨迹。
• Reflect (<|reflect|>)：提示模型暂停并验证先前推理步骤的正确性。
• Explore Alternative Solution (<|explore|>)：向模型发出信号，以识别其推理中的关键缺陷并探索新的解决方案。

每个推理步骤 ${\text{y}}_l$ 都是一个 token 序列，起始 token 可能是指定的元动作 token 之一。我们将此公式称为动作-思维链推理 (COAT)。具体而言，典型的思维链推理 (CoT) 可视为 COAT 的一个特例，其中 CoT 中的每个推理步骤都仅限于 <|continue|>，而不明确包含其他类型的元动作。
　　Learning to Reason via RL。我们将推理表述为一个序列决策问题，其中推理是一个逐步构建和细化答案的过程。具体来说，模型 ${\pi }_{\theta }$ 从输入上下文 $x$（初始状态 $z_0$）开始，生成推理步骤${\text{y}}_l$（动作），通过附加 $y_l$来更新上下文（下一个状态 $z_{l+1}=z_l\oplus {\text{y}}_l$，其中$\oplus$表示字符串连接），并重复此过程，直到产生最终答案 ${\text{y}}_L$。当模型发出完成信号（例如，EOS token）时，推理终止。最简单的奖赏函数可以是 I { y L = y ∗ } \mathbb I\{\textbf y_L = \textbf y^∗\} I{yL​=y∗}，评估最终答案 ${\text{y}}_L$ 是否与基本事实 ${\text{y}}^{\ast }$ 匹配。有了这个公式，我们可以训练模型使用RL进行推理，旨在生成最大化期望奖赏的推理步骤。然而，将RL应用于推理有两个关键挑战：

1. Unawareness of meta-action tokens：该模型不理解特殊 token 的用途，也未能认识到遇到特殊元动作 token 可能需要反思或提出替代方案。
2. Long horizon and sparse rewards：推理需要长期决策，而奖赏只在最后，这阻碍了学习效果。模型必须采取许多正确的推理步骤才能获得奖赏，而失败会迫使它从初始状态（即问题陈述）重新开始。这让学习变得困难，因为与奖赏相关的训练数据很少，但奖赏对于推动强化学习进步至关重要。

Overview of Proposed Method。为了解决模型最初对元动作 token 的不了解，我们引入了一个热身“格式微调”阶段：我们在一个包含一些已证明的推理轨迹的小型数据集上对预训练的 LLM 进行微调（第 4.1 节）。此步骤使模型熟悉使用和响应元动作 token。其次，为了应对长期和稀疏奖赏的挑战，我们提出了一种“重启和探索”（RAE）策略，灵感来自 Go-explore。在这里，模型从中间步骤重新启动，包括以前推理尝试失败的那些点，使其能够专注于纠正错误而不是从头开始。我们还添加了探索奖赏以鼓励更深入的反思，进一步增加模型得出正确答案的机会（第 4.2 节）。

4.1. Format Tuning Through Imitation Learning

训练基础 LLM ${\pi }_{\theta }$ 来执行 COAT 推理是一项重大挑战：LLM 通常不会在包含试错的 COAT 推理数据上进行预训练，因此需要一个后训练阶段来注入此功能。为了解决这个问题，我们引入了格式微调 (FT)，这是一种旨在通过模仿学习训练 LLM 模拟专家 COAT 轨迹的方法。模仿学习技术广泛应用于机器人领域，其中使用人类专家提供的演示轨迹来训练 Agent。但是，对于复杂任务而言，为 LLM 生成高质量的演示轨迹成本过高。为了有效地构建演示轨迹数据集 ${\mathcal{D}}_{syn}=\{({\text{x}}^{(i)},{\tilde{\text{y}}}^{(i)}){\}}_{i=1}^N$，我们提出了一个利用三个 LLM 的多 Agent 数据合成框架：

• Generator：给定一个输入问题，生成器 ${\pi }_g$ 使用经典的CoT技术为给定的输入问题生成多条推理路径。
• Critic：Critic ${\pi }_c$评估生成器生成的推理路径的正确性，提供反馈以改进推理并解决次优步骤。
• Reward Model：此外，奖赏模型 ${\pi }_r$ 为细化的推理路径分配分数，并选择最有效的路径作为最终的演示轨迹。

这三个模型协作构建了高质量的演示轨迹（轨迹合成的详细信息见附录 C）。对于这项工作，我们采用最简单的模仿学习方法，即行为克隆，该方法利用有监督微调在专家 COAT 演示轨迹 ${\mathcal{D}}_{syn}$ 上训练 LLM 策略。值得注意的是，我们观察到，即使数量较少（10K）的 COAT 演示轨迹也足以使 ${\pi }_{\theta }$ 有效遵循 COAT 推理格式。

4.2. Self-improvement via Reinforcement Learning

　　在格式微调后，LLM 策略 ${\pi }_{\theta }$ 采用了 COAT 推理风格，但难以推广，特别是在使用元动作进行自我反思时。这种限制源于格式微调期间样例的稀缺。虽然收集更多样例可能会有所帮助，但这样做成本高昂且耗时。相反，我们探索模型是否可以通过 RL 自我改进其推理。
　　我们从格式微调后的 LLM 开始，使用广泛使用的 RL 方法 PPO 算法对其进行训练。除了对数据集 $\mathcal{D}$ 中的问题 $\text{x}$ 进行训练外，我们还训练模型 ${\pi }_{\theta }$，使其从格式微调后的 LLM 生成的部分轨迹开始推理。由于推理错误通常源于小错误而不是根本缺陷，因此从头开始重新探索效率低下。相反，我们允许模型从中间步骤重新启动以纠正错误并最终获得正确答案。受 Go-Explore 的启发，我们引入了重启和探索 (RAE) 策略。
　　Initial States。RAE 训练模型不仅从问题陈述进行推理，而且从过去轨迹（正确和不正确）中采样的中间步骤进行推理。这使得更深入的探索无需多余的重新计算。如算法 1 所述，给定输入问题 $\text{x}\in \mathcal{D}$，格式微调后的 LLM 首先生成多个推理轨迹。然后，我们随机回溯 $T\ge 0$ 个步骤并附加一个反思token $<|reflect|>$ 以提示模型改进其推理。为了鼓励多样化的探索，正确和不正确的轨迹分别存储在重启缓冲区（${\mathcal{D}}_{restart}^{+}$ 和 ${\mathcal{D}}_{restart}^{-}$）中。然后，RL 训练优化这些缓冲区以及原始问题数据集的推理，从合并的数据集 ${\mathcal{D}}_{restart}$ 中采样初始状态。
　　Reward Design。RAE 为模型提供了多次改进推理的机会，但有效的反思是利用这些机会的关键。除了使用正确性作为奖赏外，我们还引入了以下奖赏作为提示，以引导模型得出正确答案：

• Rule-based Reward：基于规则的奖赏只是评估最终答案的正确性。
  r r u l e ( y ~ L , y ∗ ) = I y ~ L = y ∗ − 1 ∈ { − 1 , 0 } r_{rule}(\tilde{\textbf y}_L,\textbf y^*)=\mathbb I_{\tilde{\textbf y}_L=\textbf y^*}-1\in \{-1,0\} rrule​(y~​L​,y∗)=Iy~​L​=y∗​−1∈{−1,0}
• Reflection Bonuses：为了强化自我反思，我们引入了反思奖赏 $r_{bonus}$。如果模型从存储在负重启缓冲区（${\mathcal{D}}_{restart}^{-}$）中的错误推理轨迹开始并成功解决问题，它将获得奖赏，鼓励它纠正过去的错误。相反，如果它从正重启缓冲区（${\mathcal{D}}_{restart}^{+}$）中的正确轨迹开始但未能解决问题，它将受到惩罚，阻止它在已经走上正确轨道时进行不必要的修改。反思奖赏的正式定义为：
  $$r_{bonus}(z,\tilde{\text{y}})=\{\begin{array}{ll}\beta & ifz\in {\mathcal{D}}_{restart}^{-}and{\tilde{\text{y}}}_L={\text{y}}^{\ast },\\ -\beta & ifz\in {\mathcal{D}}_{restart}^{+}and{\tilde{\text{y}}}_L\ne {\text{y}}^{\ast },\\ 0,& otherwise,\end{array}$$
  其中 $\beta$ 是奖赏超参数。
• Preference Bonuses：由于在初始训练阶段正确答案很少，因此奖赏信号通常过于稀疏，无法进行有效的 RL 训练。即使经过反思，模型也可能无法生成任何正确的推理轨迹，从而导致稀赏奖励问题。为了缓解这种情况，我们使用 Bradley-Terry (BT) 偏好框架训练结果奖赏模型 (ORM)。ORM 对推理轨迹进行评级，为正确（首选）的轨迹分配更高的值。对于每个问题 $\text{x}\in \mathcal{D}$，我们使用 ${\pi }_{\theta }$ 生成多个轨迹，并通过配对正确和不正确的输出来构建偏好数据集。训练 BT 模型以最大化这些对之间的分数差距。ORM 的输出 $\sigma (r_{\psi }(z,\tilde{\text{y}}))\in [0,1]$用作细粒度奖赏信号，帮助模型进一步完善其推理。有关详细信息，请参阅附录 D.3。

对于初始状态 $z\in {\mathcal{D}}_{restart}$ 和采样轨迹 $\tilde{\text{y}}$，整体奖赏函数 $r(z,\tilde{\text{y}})$ 定义为：
$$r(z,\tilde{\text{y}})=r_{rule}({\tilde{\text{y}}}_L,{\text{y}}^{\ast })+\sigma (r_{\psi }(z,\tilde{\text{y}}))+r_{bonus}(z,\tilde{\text{y}})$$
　　Iterative Self-improvement。强化学习使策略能够从自我生成的轨迹中进行自我改进，但这也可能导致恶性循环，即策略收敛到局部次优，无法进一步改进。受 (Agarwal et al., 2022; Schmitt et al., 2018) 的启发，我们提出了一种迭代自我改进策略来缓解此问题。具体来说，在每一轮强化学习训练之后，我们通过有监督微调 (SFT) 将当前优化良好的策略的知识蒸馏到基础模型中。然后，从新微调的模型开始，我们再进行一轮强化学习训练。直观地讲，从优化的角度来看，每一轮蒸馏都可以看作是一种参数重置机制，可帮助策略在损失景观中摆脱局部最优，从而继续自我改进（更多细节包含在 D.3 节中）。在下一节中，我们将提供实证证据来验证这种方法。

5. Experiment