如何求取串并联电路的等效电阻

最基本的串并联

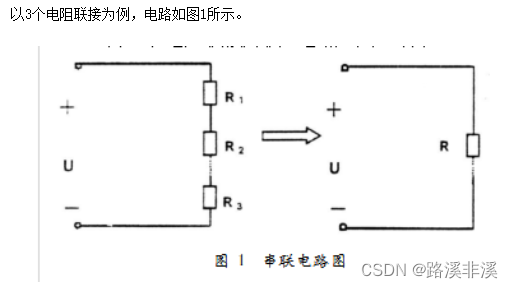
求阻值最基本的方法就是串联和并联计算，如果直接能看出来串联和并联关系，那么就能直接计算，比如：

但是在实际电路中，单纯的电阻串联或并联是不多见的，更常见的是既有串联，又有并联，即电阻的混联电路。这时候我们不容易看出电路中的串并联关系，怎么办呢？

电位点（节点）的分裂与合并

我们考虑下电阻的串联和并联有什么特点？

串联的电阻都在同一条支路上，这个没什么好说的。

并联电路有什么特点呢？

并联电路的两端每一端都处于相同的电位点上，不管导线有多长或者多短。

这个特性很重要，因为如果两端都分别处于相同的电位点，那么这个点即可以分裂，也可以合并，并不影响原来的布局，只是更方便我们查看而已。

哪怕导线是像下面红色线这样连接的，也不影响其布局结构。

也就是说，一个电位点可以在其所在的无电阻支路上随意移动。

比如这个电路

我们将相同的电位点分裂下

只要稍微将电位点分裂下，就能更加清晰地知道串并联关系了。

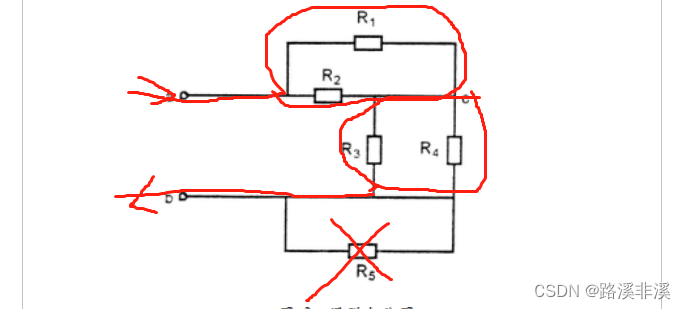
再看这个图

只要将电位相同的点做个合并就能知道，其实就是从a点出发，然后经过R1R2并联，R3R4并联，然后二者再串联，最后再经过导线回到b。

这里的R5被短了，所有电流全从没有阻碍的导线上走掉了。

这种方式适用于电阻之间联接关系比较容易确定的场合。

上面的方法也不是每种情况都有用，有时候，根本就看不出来哪些点是电位相同点。

比如

就需要更多的方法来解决这些对应的问题了。

节点命名法

例如图4所示，各电阻的串、并联关系不是很清晰，对初学者来说，直接求解比较困难。所以，可将原始电路进行改画，使之成为电阻联接关系比较明显的电路，然后再进行计算。

具体方法步骤如下：

（1）找出电路各节点，并对其进行命名，如图5所示。

在找节点时需注意：

等电位点属于同一点，故不能重复命名，如上图的c点，它是由三个等电位点构成的，命名时必须将它们看成一点。

（2）将各节点画在一条水平线上，如图6所示。

布局各节点时需注意：为方便计算，最好将两端点分别画在两头，如图6的a、b两点。

（3）对号入座各电阻，画出新电路。即将各电阻分别画在对应节点之间，这样，就构成了一个与原始电路实质相同，而形式比较简单明了的新电路了，如图7所示。最后再求等效电阻。

此方法可称为节点命名法。它是分析电阻联接关系比较复杂电路的一种实用的方法。

其本质上，还是节点的分裂和合并。

注意，从不同的端口看去，等效电阻常常是不一样的。

上面的两种方法足以应付大多数的常规电路。 

我们来看看上面的这张图，看能否用节点命名法来分析等效电阻。

来画一画

注意，上面的a点和b点有三个同电位点，属于同一个节点，不要搞错了。

从上图能看出来，变换之后，依然看不出来各电阻的串并联关系。

那就只能继续找方法了。

……

垂直对称电路的等效电阻

我们观察下面的图

利用这个方法可以化简一些对称的串并联电路，注意，对称要完全对称，而不是形状上的对称，阻值上也要对称。

画出对称线后，切到的保留，剖到的拿走。

因为切到的保留，我们也不能做什么，所以重点关注被剖到的。

先看最后一个图

这里15的电阻被剖到了，所以可以直接拿走。

就变成了这样：

之所以能拿走，是因为两侧对称，所以中间两点的电位是相同的，没有电压也就没有电流，相当于开路。

这样化简之后，就能看到更明显的串并联关系。

再看这个图

貌似没有被剖的电阻。

其实，这里的剖，并不一定是电阻，也可以剖“线”

根据等电位点的分裂和合并，可以将该电路最下面的点做个分裂，有两种分法：

可以看到，第二种分裂法，下面的连接线就被剖了。

所以，此时那根线可以去掉。

就变成了下面的等效图

这样，就能更好地看出串并联关系了。

再来看看这张图

这个电路图就是上下完全对称的，上下的阻值都一样。

所以，中间一条横线上的三个点，电位都是相同的，这样，两个7电阻两端的电压其实是0，也就没有电流流过，相当于开路。

因此，这个电路图等效图如下：

其实，画线后就知道对称线剖了这两个7电阻，所以可以直接拿掉。

水平对称电路的等效电阻

观察下方的电路图

像这种，直接连接两个端点，连线两侧完全对称的电路一般就叫做水平对称电路。

水平对称电路中，两个绿色点电位相同，两个黄色点电位相同。

因此，两侧电阻实际都是并联关系，据此可以算出并联电阻值，然后保留一侧。

如下：

化简后可以更好地看出串并联关系。

电桥结构求解等效电阻

上面两个对称电路的等效电阻的求解方法，是针对一些特殊情况的，并不具有普遍性。

下面介绍一种电桥结构电路。

通常，如果电路中无法看出明显的串并联结构，就可以考虑下是不是存在电桥结构。

电桥结构的识别：

从目标端口看进去，其中好像是有两对电阻串联，但却刚好被一个电阻给割断了。

看看不同的画法，其本质都是电桥。

……

上面这几张图都是电桥结构。

根据我们对惠斯通电桥的了解，当R1/R2=R3/R4时，电桥处于平衡状态，此时R5处于断开状态，也就是说，可以直接去掉。

比如：

这时候，就能更好地看出串并联关系了。

再比如：

本质上就是两点电位相同。

这种方法仍然具有局限性，当电桥处于非平衡状态时，就没法处理了。

比如：

这时候怎么办呢？

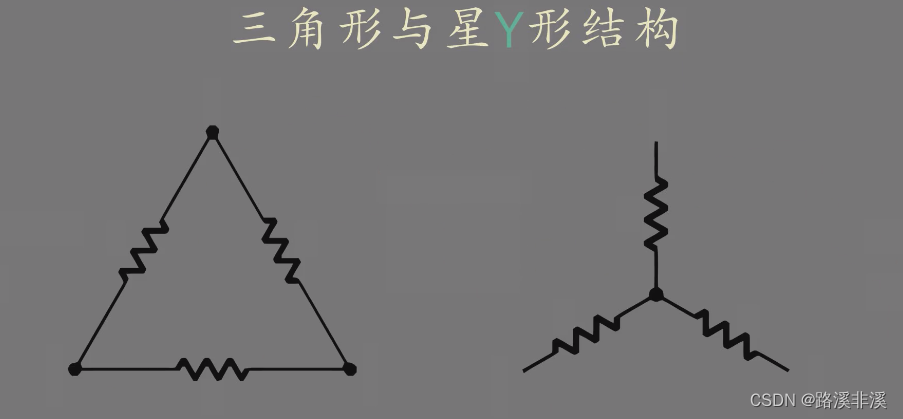
三角形结构和星形结构的互换

三角形结构有时候就写成△结构；

星形结构有时候也叫做Y结构；

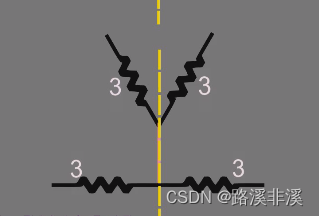
当我们用上面的办法都不能求解等效电阻时，就可以尝试将电路结构变一变，然后再去求解等效电阻。

关键是要记住红框里的规律，不能死记公式。

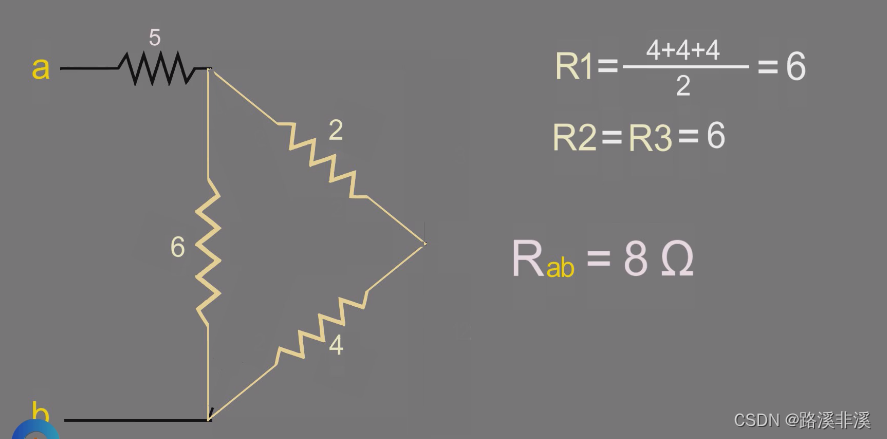
举例说明1

左边的电路中就有两个三角形结构，如右图所示

转换

此时，就能更好地看出串并联关系了。

举例说明2

这个图里其实也有Y形结构

这种变形其实是可以根据基尔霍夫定律推导出来的。

总结

1

上面的节点分裂与合并、节点命名法能解决大部分的常规电路；

2

垂直对称、水平对称、电桥结构适用于特殊场景，这三者的本质都是因为对称和比例相同所引申出的电位相同，然后可以去掉其中一些电阻或者连线；

3

三角形和星形结构是在电路中无法找到串并联关系时，尝试改变电路结构；

……

不管是哪种方法，都是为了让我们更好地看出电路中的串并联关系。